General Theory of Information Transfer

Information in Natural Science, Social Science Humanities and Engineering

P. Algoet: Universal Parsimonious Prequential Modeling Schemes for Stationary Processes with Densities

Let $\mu(dx)$ be a normalized reference measure on a standard Borel space ${\mathcal X}$ and let ${\sf P}$ be a probability measure on the sequence space ${\mathcal X}^\mathbb{Z}$ such that for all $n\ge 1$ , the marginal distribution $P(dx^n)=P(dx_0)P(dx_1\mid x_0)\ldots P(dx_{n-1}\mid x_0 x_1\ldots x_{n-2})$ of the segment $X^n=(X_0,X_1,\ldots,X_{n-1})$ admits a density

$\begin{displaymath}p(x^n)=p(x_0)p(x_1\mid x_0)\ldots p(x_{n-1}\mid x_0x_1\ldots x_{n-2})\end{displaymath}$

$\begin{displaymath}\lim_{n\to\infty}\,{1\over n}\log p(X^n)={\sf I}_\mu({\sf P}){\quad\hbox{a.s.}}[{\sf P}]\end{displaymath}$

A prequential (sequential predictive) modeling scheme is a sequence of conditional probability densities $\{q(x_t\mid x^t)\}_{t\ge 0}$ . The compounded likelihood $q(x^n)=q(x_0)q(x_1\mid x_0)\ldots q(x_{n-1}\mid x_0 x_1\ldots x_{n-2})$ cannot grow faster than exponentially with limiting rate ${\sf I}_\mu({\sf P})$ :

$\begin{displaymath}\limsup_{n\to\infty}\,{1\over n}\log q(X^n)\le \lim_{n\to\inf... ... n}\log p(X^n) ={\sf I}_\mu({\sf P}){\quad\hbox{a.s.}}[{\sf P}]\end{displaymath}$

$\begin{displaymath}\lim_{n\to\infty}\,{1\over n}\log \hat p(X^n)={\sf I}_\mu({\sf P}){\quad\hbox{a.s.}}[{\sf P}]\end{displaymath}$

$\begin{displaymath}\lim_{n\to\infty}\,{1\over n}\log \left({p(X^n)\over \hat p(X... ...=0{\quad\hbox{a.s.}}[{\sf P}] \quad\hbox{and in $L^1({\sf P})$}\end{displaymath}$

$\begin{displaymath}\lim_{n\to\infty}\,{1\over n}I(P_{X^n}\mid \hat P_{X^n})=0\end{displaymath}$

We construct a universal parsimonious prequential modeling scheme for stationary processes with densities using the following ingredients.
1. The universal data compression algorithm of Lempel and Ziv is used to construct universal prequential modeling schemes for quantized versions of the process $\{X_t\}$ .
2. A prequential modeling scheme for a quantized version can be lifted to a prequential modeling scheme for the process itself according to the minimum divergence principle.
3. Several modeling schemes for the process $\{X_t\}$ are combined into a mixture. This is the essence of Bayesian modeling.
4. The information divergence rate ${\sf I}_\mu({\sf P})$ of the process $\{X_t\}$ is equal to the maximum information divergence rate of quantized versions of the process (Pinsker's formula).

Parsimonious prequential modeling schemes provide the solution to the following problems.
1. Universal procedures for discrimination or hypothesis testing. Suppose the null hypothesis $\mu$ is rejected in the event $B_n=\{\hat p(X^n)\ge e^{nD}\}$ . Then $\mu$ will be rejected eventually almost surely whenever $\{X_t\}$ is stationary ergodic with distribution ${\sf P}$ satisfying ${\sf I}_\mu({\sf P})>D$ . The probability $\mu(B_n)$ that $\mu$ is incorrectly rejected when in fact $\mu$ is the true distribution of $\{X_t\}$ is bounded by $e^{-nD}$ .
2. Universal gambling schemes. Suppose a gambler bets on each outcome

with knowledge of the past

according to the conditional probability density $\hat p(x_t\mid X^t)$ relative to the odds measure $\mu(dx_t)$ . The gambler's capital will be returned multiplied by the factor $\hat p(X_t\mid X^t)$ when the outcome

is revealed. The gambler doesn't know the true process distribution ${\sf P}$ , but he learns from experience in such a way that his compounded capital $\hat p(X^n)=\hat p(X_0)\hat p(X_1\mid X_0)\ldots \hat p(X_{n-1}\mid X_0 X_1\ldots X_{n-1})$ grows exponentially almost surely with the maximal rate ${\sf I}_\mu({\sf P})$ that could be asymptotically attained if he knew the infinite past $X^{-1}_{-\infty}$ and hence the process distribution ${\sf P}$ to begin with.
3. Universal data compression. A parsimonious prequential modeling scheme for $\{X_t\}$ can be used to design a universal data compression algorithm for quantized versions of $\{X_t\}$ . We can design uniquely decipherable variable-length binary codes for quantized blocks of increasing length in such a way that the per-symbol description length approaches the entropy rate of the quantized process.
4. Consistent estimation of $p(x_0\mid X^{-1}_{-\infty})$ . Given a parsimonious prequential modeling scheme $\{\hat p(x_t\mid x^t)\}_{t\ge 0}$ , define

$\begin{displaymath}\bar p(x_0\mid X^{-1}_{-n})={1\over n}\sum_{0\le t<n}\hat p(x_0\mid X^{-1}_{-t})\end{displaymath}$

$\begin{displaymath}\lim_{n\to\infty}\,{\sf E}\,I(P_{X_0\mid X^{-1}_{-\infty}}\mid \bar P_{X_0\mid X^{-1}_{-n}})=0\end{displaymath}$

I. Althöfer: On the Design of Multiple Choice Systems: Shortlisting in Candidate Sets

Definition (``Multiple Choice System for Decision Support''): Programs compute a clear handful of candidate solutions. Then a human has the final choice amongst these candidates.

We shortly call such systems ``Multiple Choice Systems''. In the field of electronic commerce Multiple Choice Systems are/were sometimes advertised under the names ``Recommender System'' and ``Recommendation System''.

We describe three different Multiple Choice Systems which were very successful in the game of chess.

``3-Hirn'' / ``Triple Brain'': Two independent programs make one proposal each.

``Double-Fritz with Boss'': Since 1995 the chess program ``Fritz'' has a 2-best-mode where it computes not only its best but also its second best candidate move. The human gets the choice amongst these top-2 candidates.

``Listen-3-Hirn'' / ``List Triple Brain'': Two independent chess programs are used which both have k-best modes. Program 1 proposes its k best candidate moves, whereas program 2 gives its top m candidates. (The numbers k and m are chosen appropriately, for instance k=m=3.)

In all three examples the human has the final choice amongst the computer proposals. However, he is not allowed to outvote the programs.

The speaker is an amateur chess player (rating = 1900 +- epsilon) and experimented with these Multiple Choice Systems in performance-oriented chess: with 3-Hirn from 1985 to 1996, Double-Fritz with Boss in 1996, List Triple Brain in 1997. The systems almost always performed 200 rating points above the performances of the single programs in it. The ``final'' success was a 5-3 match win of List Triple Brain over Germany's no. 1 player Arthur Yusupov (Elo 2645 in those days) in 1997. After this event top human players were no longer willing to play against these Multiple Choice Systems.

Claim: In a Multiple Choice System the human is not allowed to outvote the program. This often helps to improve the performance, especially in realtime applications.

Natural building blocks of a Multiple Choice System are programs that compute more than one candidate solution. In this context k-best algorithms are often not suited because they tend to give only micro mutations instead of true alternatives (master example: the shortest path problem). The task to generate true alternatives of ``good'' quality is typically non-trivial.

The talk will center around the problem of finding true alternatives in large candidate sets.

R. Apfelbach: Chemical communication in mammals: What we know and what we would like to know

Chemical regulation of cellular processes makes its appearance in some of the most primitive plant and animal species. Chemical regulatory agents include relative nonspecific molecules such as CO2, H+, O2 and Ca2+, and those, like cAMP, that are more complex and are produced specifically as regulators, or messengers. Chemical messengers operate at all levels of biological organization from subcellular to interorganismal. Some animal species, for example, utilize chemical messengers as means of communication between individuals of that species. In this case we call chemical messengers as pheromones.

In the talk we first will look at the sender of chemical signals. Topics to be covered include: Chemistry of pheromones, where are pheromones produced and how are they released; what kind of information do pheromones convey? The second aspect of the talk will concentrate on the receiving station. Where and how are chemical signals received? We will follow the chemical signals from the receptor to the brain. Topics to be covered include: the receiving structure (olfactory epithelium), the processing station (olfactory bulb) and olfactory coding.

The talk will concentrate on selected mammalien species. However, some differences and similarities between invertebrates and vertebrates will be indicated.

The problem of characterizing and detecting recurrent sequence patterns such as substrings or motifs and related associations or rules is variously pursued in order to compress data, unveil structure, infer succinct descriptions, extract and classify features, etc. In Molecular Biology such regularities have been implicated in various facets of biological function and structure. The discovery, particularly on a massive scale, of significant patterns and correlations thereof poses interesting methodological and algorithmic problems, and often exposes scenarios in which tables and descriptors grow faster and bigger than the phenomena they are meant to encapsulate. This talk reviews some results at the crossroads of statistics, pattern matching and combinatorics on words that enable us to control such paradoxes, and presents related constructions, implementations and empirical results.

We define and show how to construct nonbinary quantum stabilizer codes. Our approach is based on nonbinary error bases. It generalizes the relationship between selforthogonal codes over

and binary quantum codes to one between selforthogonal codes over

and

-ary quantum codes for any prime power

R. Ahlswede, H. Aydinian, and L.H. Khachatrian: On Bohman's conjecture related to a sum packing problem of Erdos

Motivated by a sum packing problem of Erdos, Bohman discussed a problem which seems to have an independent interest. Let

be a hyperplane in $\mathbb{R}^n$ such that $H\cap\{0,\pm1\}^n=\{0^n\}$ . The problem is to determine

$\begin{displaymath} f(n)\triangleq\max_H\vert H\cap\{0,\pm1,\pm2\}^n\vert.\end{displaymath}$

$\begin{displaymath} f(n)=1/2(1+\sqrt2)^n+1/2(1-\sqrt2)^n.\end{displaymath}$

V. B. Balakirsky: Hashing of Databases with the Use of Metric Properties of the Hamming Space

We describe hashing of databases as a problem of information and coding theory. It is shown that the triangle inequality for the Hamming distances between binary vectors can essentially decrease the computational efforts needed to search for a pattern in databases. Introduction of the Lee distance of the Hamming distances, leads to a new metric space where the triangle inequality is effectively used.

V.B. Balakirsky and A.J.H. Vinck: On the performance of permutation codes for multi-user communication

The permutation coding for multi-user communication schemes that originate from a Fast Frequency Hopping / Multiple Frequency Shift Keying modulation is investigated. Each sender is either passive or he sends some signal formed as a concatenation of

elementary signals having

different specified frequencies. There is also a jammer who can introduce disturbances. A single disturbance is either sending of the signal containing all

frequencies at a certain time instant or sending of some elementary signal at all time instants. Each receiver receives a vector of

sets where the set at each time instant contains a fixed frequency if and only if corresponding elementary signal was sent either by some sender or by the jammer. The task of the receiver is unique decoding of the message of his sender.

We present regular constructions for permutation codes for this scheme given the following parameters: the number of frequencies, the number of pairs (sender, receiver), the number of messages per sender, the maximum number of disturbances of the jammer.

We analyze iterative decoding of codes constructed from bipartite graphs with good expansion properties. For code rates close to capacity of the binary symmetric channel we prove a new estimate that improves previously known results for expander codes and concatenated codes.

V. Blinovsky: New Approach to the Estimation of the probability of Decoding Error

We offer a new approach of deriving lower bounds for the probability of the decoding error in the discrete channel without memory for zero rate. This approach allows to essentially simplify the process of obtaining the bound making it natural and at the same time to improve the rest term of the estimation. Consider the discrete channel without memory, which is determined by the set of conditional probabilities ${\cal P}=\{ p(i\vert j);\ i=1,2,\ldots , K\}$ , on the finite set $[N]=\{ 1,2,\ldots ,M\}$ . The set ${\cal P}$ generates the set of condition probabilities

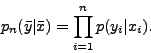
$\begin{displaymath} p_{n} (\bar{y}\vert\bar{x}) =\prod_{i=1}^{n}p(y_{i}\vert x_{i}). \end{displaymath}$

The maximal probability of the decoding error $P_{e}(G)$ is defined by the relation

$\begin{displaymath} P_{e}(G)=\max_{i}P_{e}(i,G), \end{displaymath}$

$\begin{displaymath}P_{e}(i,G )=\sum_{\bar{y}\not\in A_{i}}p_{n}(\bar{y}\vert\bar{a}_{i}) \end{displaymath}$

$\begin{displaymath} P_{e}(M,n)=\min_{{\cal G}:\vert{\cal G}\vert\geq M}P_{e}({\cal G}) \end{displaymath}$

In the work [1] the central result which was obtained by Shannon, Gallager and Berlecamp was the proof of the following bound:

		$\displaystyle \ln P_{e}(M,n)\geq -n\biggl[ E_{ex}^{+}) +\frac{2d_{{\max}}\sqrt{K}}{\sqrt{\lceil\log\log M \rceil}}+$	(1)
	$\textstyle +$	$\displaystyle \sqrt{\frac{2}{n}}\ln\frac{1}{P_{\min}}+\frac{\ln 4}{n}\biggr] ,$

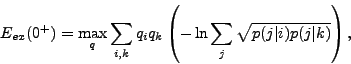
$\begin{displaymath} E_{ex}(0^{+})=\max_{q}\sum_{{i,k}}q_{i}q_{k}\left( -\ln\sum_{j}\sqrt{p(j\vert i)p(j\vert k)}\right) , \end{displaymath}$

In present work we offer an approach which seems to us more natural and which allows us to obtain the bound

$\begin{displaymath} \ln P_{e}(M,n)\geq -n\biggl[ E_{ex}(0^{+})+\sqrt{\frac{2}{n}... ...lta}{\ln M}}+2\sqrt{\delta}+2\delta\right)\frac{1}{2}\biggr] . \end{displaymath}$

(2)

We do the research of the probabilistic properties of random packing in Euclidean space.

For the locally finite set $\sigma\subset R^{n}$ and cube $K_{N}$ with the center at $0\in R^{n}$ and edge

define $\sigma_{N}=\sigma \bigcap K_{N}$ and let

$\begin{displaymath} d(\sigma_{N})=\min_{x,x'\in\sigma_{N};x\neq x'}\vert\vert x-x' \vert\vert. \end{displaymath}$

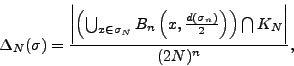
$\begin{displaymath} \Delta_{N}(\sigma )=\frac{\biggl\vert \left(\bigcup_{x\in\si... ...ma_{n})}{2}\right)\right)\bigcap K_{N}\biggr\vert}{(2N)^{n}}, \end{displaymath}$

$\begin{displaymath}\Delta(\sigma )=\limsup_{N\rightarrow\infty}\Delta_{N}(\sigma ). \end{displaymath}$

$\begin{displaymath}\delta (\sigma)=- \lim_{n\rightarrow\infty}\frac{\log_2 \Delta (\sigma )}{n}.\end{displaymath}$

$\begin{displaymath} \chi_{d}(x,x' )\left\{\begin{array}{ll} 1,& if \vert\vert x-... ...,\\ 0, & if \vert\vert x-x' \vert\vert >d , \end{array}\right.\end{displaymath}$

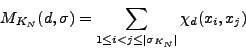
$\begin{displaymath} M_{K_{N}}(d,\sigma)=\sum_{1\leq i<j\leq \vert \sigma_{K_{N}}\vert}\chi_{d}(x_{i},x_{j}) \end{displaymath}$

$\begin{displaymath} D(M_{K_{N}}(d,\sigma ))=E(E((M_{K_{N}}-E(M_{K_N}))^2\vert\v... ...\vert=m))=v_{n}(d)(2N)^{n}\left( \frac{1}{2}+v_{n}(d) \right) .\end{displaymath}$

(3)

$\begin{displaymath} D(M_{K_N})<C(n)(2N)^n .\end{displaymath}$

Next we consider a natural generalization of the previous situation. We say that the locally finite subset $\sigma (L) \subset R^n$ is

packing if for arbitrary

points $\{ x_i ;i=1,2,\ldots ,L+1\}\subset\sigma(L)$ the following relation is valid

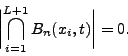
$\begin{displaymath}\biggl\vert\bigcap_{i=1}^{L+1} B_n (x_i ,t)\biggr\vert =0 . \end{displaymath}$

$\begin{eqnarray*} \sigma_{K_N} (L) &=& \sigma (L)\bigcap K_N , \end{eqnarray*}$

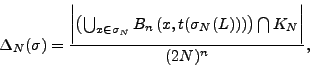
$\begin{displaymath} \Delta_{N}(\sigma )=\frac{\biggl\vert \left(\bigcup_{x\in\s... ...sigma_N (L))\right)\right)\bigcap K_{N}\biggr\vert}{(2N)^{n}}, \end{displaymath}$

$\begin{displaymath}\Delta(\sigma )=\limsup_{N\rightarrow\infty}\Delta_{N}(\sigma ). \end{displaymath}$

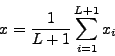
$\begin{displaymath} x=\frac{1}{L+1}\sum_{i=1}^{L+1}x_i \end{displaymath}$

$\begin{displaymath} r^2 =\frac{1}{L+1}\sum_{i=1}^{L+1}(x_i -x)^2 =\frac{1}{L+1} \sum_{i=1}^{L+1}x_{i}^{2}-x^2. \end{displaymath}$

(4)

$\begin{displaymath} \biggl\vert\bigcap_{i=1}^{L+1}B(x_i ,r)\biggr\vert =0 . \end{displaymath}$

(5)

$\begin{displaymath}\chi_{i_1 ,i_2 ,\ldots ,i_{L+1}}(t)=\left\{\begin{array}{ll} ... ...(x_i ,t)\biggr\vert =0 ,\\ 0, & otherwise. \end{array}\right. \end{displaymath}$

$\begin{displaymath}P(\chi_{i_1 ,i_2 ,\ldots ,i_{L+1}}(r)=1)=\int\ldots\int_{\sum_{i=1}^{L+1} (x_{i}-x)^2 \leq r(L+1)}dx_1 dx_2 \ldots dx_{L+1}. \end{displaymath}$

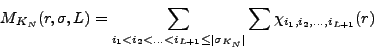
$\begin{displaymath}M_{K_{N}}(r,\sigma ,L)=\sum_{i_1 <i_2 <\ldots <i_{L+1}\leq \vert\sigma_{K_{N}}\vert} \sum\chi_{i_1 ,i_2 ,\ldots ,i_{L+1}}(r) \end{displaymath}$

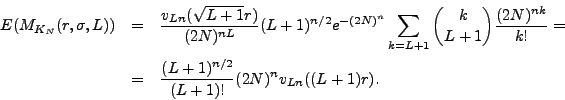
$\begin{eqnarray*}E(M_{K_{N}}(r,\sigma ,L))&=&\frac{v_{Ln}(\sqrt{L+1}r)}{(2N)^{nL... ...k}}{k!}=\\ &=&\frac{(L+1)^{n/2}}{(L+1)!}(2N)^{n}v_{Ln}((L+1)r). \end{eqnarray*}$

$\begin{displaymath} (L+1)^{n/2}v_{Ln}(\sqrt{L+1}r)=1, \end{displaymath}$

(6)

$\begin{displaymath}\Delta =v_{n}(r)\left( 1-\frac{1}{(L+1)!}\right).\end{displaymath}$

$\begin{displaymath}v_{n}^{L}(r)\frac{(\pi n)^{(L-1)/2}}{L^{1/2}}\left(\frac{(L+1)^{L+1}}{L^{L}}\right)^{n/2}(1+o(1)). \end{displaymath}$

$\begin{displaymath}\frac{\ln v_{n}(r)}{n}=\frac{1}{2}\ln\left(\frac{L}{(L+1)^{1+1/L}}\right)(1+o(1)) \end{displaymath}$

$\begin{displaymath}\frac{\ln\Delta}{n} =\frac{1}{2}\ln\left(\frac{L}{(L+1)^{1+1/L}}\right)(1+o(1)).\end{displaymath}$

We calculate the variation of the random variable $M_{K_N}(\tau,\sigma ,L)$ . We can say almost nothing about the behavior of the asymptotic of the normalized $M_{K_N}$ as $N\rightarrow\infty$ as it was done in the case of

Would a thorough understanding of the Language Acquisition Device (LAD) tell us why language has the structure it does? This presentation will introduce work that suggests cultural dynamics, in conjunction with biological evolution, make the relationship between linguistic structure and the LAD non-trivial.

R. Ahlswede and N. Cai: Watermarking identification codes with related topics on common randomness (see [B4])

J.P. Allouche, M. Baake, J. Cassaigne, and D. Damanik: Palindrome complexity

One way to measure the degree of ``complication'' of an infinite word

is to associate to it a function

called subword complexity. This function counts the number of finite subwords (blocks of consecutive letters) contained in

according to their length

. We are interested here in a particular class of subwords, the palindromes, words that remain unchanged when read from right to left. By counting the number of palindromes that occur in

, one defines a new function

, the palindrome complexity. This function has some applications in theoretical physics.

We shall first present several simple examples that illustrate the different possible behaviours of the function

, and show that this function conveys information about the infinite word that cannot be deduced from

alone. Then we shall establish an inequality between the two functions, and show through other examples that this inequality cannot be substantially improved.

F. Cicalese, L. Gargano, and U. Vaccaro: Optimal approximation of uniform distributions with a biased coin

Given a coin of bias

we consider the problem of generating probability distributions which are the closest to the uniform one, using flips of the given coin. We provide a simple greedy algorithm that, having in input bits produced by a coin of bias

, produces in output a probability distribution of minimum distance from the uniform one, under several different notions of distance among probability distributions.

S. Csibi and E.C. van der Meulen: Properties of codes for identification via a multiple access channel under a word-length constraint (see also [B8])

The purpose of the present exposition is two-fold: (i) to consider a published and an as yet unpublished approach by the authors on suppressing drastically the false identification probability of huge finite length identification plus transmission codes, and (ii) to revisit published results also by the present authors on the possibilities of conveying codewords through a kind of multiple access erasure channel exhibiting, by its properties, particular flexibility. The considered suppression of the false identification probability might be viewed, in a sense, as an elementary way of forward error control designed, especially for the considered huge size identification codes, under a word length constraint. The considered kind of multiple access is controlled, both at the place of the single input and at all outputs, by the very same protocol sequence of closely least length. We rely in the present exposition essentially upon pioneering findings by Ahlswede and Dueck (1989a, 1989b), Han and Verdu (1992 and 1993) on the concatenation version of the two explicit code constructions proposed by Verdú and Wei (1993). For generating a cyclically permutable control sequence, and for giving an upper bound on the least length of such sequences we rely upon Nguyen, Györfi, Massey (1992). A lower bound on the said least length is obtained by extending a fundamental approach by Bassalygo and Pinsker (1983). The considered way of identification via an MA channel might be of interest for certain perspective remote alarm services. - Standard identification tasks are considered in the present exposition only. However, we still have got another interesting class of networking examples which might be formulated, perhaps, as

-identification tasks. See Ahlswede (1997).

The science of thermodynamics is concerned with understanding the properties of inanimate matter in so far as they are determined by changes in temperature. The Second Law asserts that in irreversible processes there is a uni-directional increase in thermodynamic entropy, a measure of the degree of uncertainty in the thermal energy state of a randomly chosen particle in the aggregate. The science of evolution is concerned with understanding the properties of populations of living matter in so far as they are regulated by changes in generation time. Directionality theory, a mathematical model of the evolutionary process, establishes that in populations subject to bounded growth constraints, there is a uni-directional increase in evolutionary entropy, a measure of the degree of uncertainty in the age of the immediate ancestor of a randomly chosen newborn. I will review the mathematical basis of directionality theory and analyse the relation between directionality theory and statistical thermodynamics. By exploiting an analytic relation between temperature and generation time, I will show that the directionality principle for evolutionary entropy is a non-equilibrium extension of the principle of a uni-directional increase of thermodynamic entropy. The analytic relation beween these directionality principles is consistent with the hypothesis of the equivalence of fundamental laws as one moves up the hierarchy, from aggregates of inanimate matter where the thermodynamic laws apply, to a population of replicating entities (molecules, cells higher organisms), where evolutionary principles prevail.

R. Ahlswede, L. Bäumer, and C. Deppe: Information theoretic models in language evolution (included in [B4])

The human language is used to store and transmit information. Therefore there is a significant interest in the mathematical models of language development. These models shall explain how natural selection can lead to the gradual emergence of human language. Among others Nowak et al. created a mathematical model, where the fitness of a language is introduced. For this model they showed if signals can be mistaken for each other, then the performance of such systems is limited. The performance can not be increased over a fixed threshold by adding more and more signals. Nevertheless the concatenation of signals or phonemes to words increases significantly the fitness of the language. The fitness of such a signalling-system depends on the number of signals and on the probabilities to transmit individual signals correctly. In the papers of Nowak et al. optimal configurations of signals in different metric spaces were investigated. Nowak conjectures that the fitness of a product-space is equal to the product of the fitnesses of the metric spaces. We analyse the Hamming model. In this model the direct consequence of Nowak's conjecture is that the fitness of the whole space equals the maximal fitness. We show that the fitness of Hamming codes asymptotically achieves this maximum.

These theoretical models of fitness of a language enable the investigations of classical information theoretical problems in this context. In particular this is true for feedback problems, transmission problems for multiway channels etc. In the feedback model we developed we show that feedback increases the fitness of a language.

A.G. D'yachkov and P.A. Vilenkin: Statistical Estimation of Average Distances for the Insertion-Deletion Metric

Using the Monte Carlo method and computer simulation, we construct and calculate point estimators and confidence intervals for average distance fractions in the space of

-ary

-sequences with insertion - deletion metric (ID metric) [1]. These unknown fractions are cut-off points for hypothetical lower bounds on the rate of codes for ID metric.

S. Galatolo: Algoritmic information content, dynamical systems and weak chaos

By the use of the Algorithmic Information Content (otherwise called Kolmogorov -Chaitin complexity) of a string it is possible to define local invariants of dynamical systems. The local invariant measures the complexity of the orbits.

We will see some relations between orbit complexity and other measures of chaos (such as entropy, initial condition sensitivity and dimension). These relations between complexity, sensitivity and dimension give a non-trivial information even in the weakly chaotic (0-entropy) case.

E. Haroutunian and A. Ghazaryan: On the Shannon cipher system with a wiretapper guessing subject to distortion and reliability

We investigate the problem of wiretapper's guessing with respect to fidelity and reliability criteria in the Shannon cipher system.

Encrypted messages of a discrete memoryless source must be communicated by a public channel to a legitimate receiver. The key-vector independent of source messages is transmitted to encrypter and to decrypter by the special secure channel protected against wiretappers. The transmitter encodes the source message and key-vector and sends a cryptogram over a public channel to a legitimate receiver which based on the cryptogram and key-vector recovers the original message by the decryption function. The wiretapper that eavesdrops a public channel aims to decrypt the original source message in the framework of given distortion and reliability on the base of csyptogram, source statistic and encryption function. The security of the system is measured by the expected number of wiretapper's guesses. The problem is to determine the minimum (over all guessing lists) of the maximal (over all encryption functions) expected number of sequential wiretapper's guesses until the satisfactory message will be found.

The guessing problem was first considered by Massey (1994). This problem subject to fidelity criterion was studied by Arikan and Merhav (1998).

The investigated problem was proposed by Merhav and Arikan (1999) and is the extension of the problem considered by them in 1999. The main extension is consideration of the distortion and reliability criteria and of the possibility to limit the number of wiretapper's guesses, that is we demand that for a given guessing list, distortion level $\Delta\geq O$ and reliability

the probability that distortions between blocklength

source messages and each of first

guessing vectors will be larger than $\Delta$ , must not exceed $2^{-NE}$ .

For given key rate

, the minimum (over all guessing lists) of the maximal (over all encryption functions)

and expected number of required guesses, with respect to distortion and reliability criteria, are found.

For the special case of binary source and Hamming distortion measure the expected number of wiretapper's guesses is calculated.

Understanding of the multipartite quantum entanglement, is currently one of the major problems in quantum information science. Progress in tis area is needed for both developing theory of quantum information science and for understanding of computation and communication power of quantum information processing.

In the talk we first demonstrate complexity of the problem and its importance for various areas of quantum information science. Then we discuss a variety of basic general approaches how to deal with the problem - approaches that are of broader importance for the field. Finally, we concentrate on some major results in this area and various open problems.

C. Mauduit and A. Sárközy proposed the use of well-distribution measure and correlation measure as measures of pseudorandomness of finite binary sequences. In this paper we will introduce and study a further measure of pseudorandomness: the symmetry measure. First we will give upper and lower bounds for the symmetry measure. We will also show that there exists a sequence for which each of the well-distribution, correlation and symmetry measures are small. Finally we will compare these measures of pseudorandomness.

Very important properties of each communication channel are characterized by the reliability function

, which was introduced by Shannon 1959, as the optimal coefficient of the exponential decrease

A big number of works is devoted to studying of this function for various communication systems. Along with achievements in this part of Shannon theory a lot of problems remain unsolved. Because of principal difficulty of finding the reliability function for whole range of rates

, this problem is completely solved only in rather particular cases. The situation is typical when (for example, for the binary symmetric channel) obtained upper and lower bounds for function

coincide only for small rates.

E. Haroutunian proposed and developed an approach, which consists in studying the function

, converse to

(Haroutunian 1967, 1969, 1982). This is not only a mechanical permutation of roles of independent and dependent variables, since the investigation of optimal rates of codes, ensuring when

increases the error probability exponential decrease with given exponent (reliability)

, may be sometimes more expedient than the study of the function

. The definition of the function

is in natural conformity with the Shannon's notions of the channel capacity

. So by analogy with the definition of the capacity this characteristic of the channel may be called

-capacity. On the other side the name rate-reliability function is also logical.

Concerning to bounds construction methods, it is found that the Shannon's random coding method (Shannon 1948) of proving the existence of codes with definite properties, can be applied with the same success for studying of the rate-reliability function. For the converse coding theorem type upper bounds deduction (so called sphere packing bounds) E. Haroutunian 1967, 1982 proposed a simple combinatorial method, which was later applied to various complicated systems.

The two-way channel was first investigated by Shannon 1961. The channel has two terminals and the transmission in one direction interferes with the transmission in the opposite direction. The sources of two terminals are independent. The encoding at each terminal depends on both the message to be transmitted and the sequence of symbols received at that terminal. Similarly the decoding at each terminal depends on the sequence of symbols received and sent at that terminal.

The restricted version of TWC is considered, where the transmitted sequence from each terminal depends only on the message but does not depend on the received sequence at that terminal.

The RTWC also was first investigated by Shannon 1961, who obtaind the capacity region

of the RTWC. The capacity region of the general TWC is not found up to now. Important results relative to various models of two-way channels were obtained by Ahlswede 1971, 1973, 1974, Dueck 1978, 1979, Han 1984, Sato 1977 and others. In particular, Dueck has demonstrated that the capacity regions for average and maximal error probabilities do not coincide.

The outer and inner bounds for $\bar C(E,W_T)$ are constructed. The limit of $\cal R_r(E,W_T)$ , when $E_1\to0$ , $E_2\to0$ , coincides with the capacity region of RTWC found by Shannon.

Shannon 1961 considered also another version of the TWC, where the transmission of information from one sender to its corresponding receiver may interfere with the transmission of information from other sender to its receiver, which was later called interference channel.

The general interference channel differs from the TWC in two respects; the sender at each terminal do not observe the outputs at that terminal and there is no side information at the receivers.

Ahlswede 1973, 1974 obtained bounds for capacity region of GIFC. The papers of Carleial 1975, 1978, 1983 are also devoted to the investigation of IFC, definite results are obtained in series of other works, but the capacity region is found only in particular cases.

The random coding bound of

-capacity region in the case of average error probability for GIFC is obtained.

Broadcast channels were first studied by Cover 1972. The capacity region of deterministic BC was found by Pinsker 1978 and Marton 1979. The capacity region of the BC with one deterministic component was defined independently by Marton 1979 and Gelfand and Pinsker 1980. The capacity region of assymmetric BC was found by Körner and Marton 1977. In many words several models of BC have been considered, but the capacity region of BC in the situation, when two private and one common messages must be transmitted, is still not found. Willems 1990 proved that the capacity regions of BC for maximal and average error probabilities are the same.

It is proved that the region $\cal R_r(E,W_B)$ is an inner estimate for

-capacity region of BC.

When $E_1\to0$ , $E_2\to0$ , using time sharing arguments we obtain the inner bound for the capacity region $\cal C(W_B)$ of BC, obtained by Marton 1979.

There exist various configurations of the multiple-access channel. The most general model of the MAC: the MAC with correlated encoder inputs, was first studied by Slepian and Wolf 1973. Three independent sources create messages to be transmitted by two encoders. One of the sources is connected with both encoders and each of the othe two is connected with only one of the encoders.

Dueck 1978 has shown that in general the maximal error capacity region of MAC is smaller than the corresponding average error capacity region. Determination of the maximal error capacity region of the MAC in various communication situations is still an open problem.

The inner and outer bounds for

-capacity region of MAC with correlated encoders are constructed. When $E\to0$ , we obtain the inner and outer estimates for the channel capacity region, the expressions of which are similar but differ by the probability distributions

and

. The inner bound coincides with the capacity region.

As special cases the regular MAC, Asymmetric MAC, MAC with cribbing encoders and channel with two senders and two receivers are considered.

P. Harremoes and F. Topsoe: Information theoretic aspects of Poisson's law (see [B47])

Current progress in integrated circuit fabrication, and nanotechnology more generally, promises to bring engineering to the quantum realm within the next two decades. To fully realize the potential of these technologies it will be necessary to develop the theoretical and experimental tools needed for the coherent control of quantum systems. The ultimate goal is a quantum computer, which will be able to perform conditional logic operations over coherent superpositions of states, thereby attaining a degree of parallelism which grows exponentially with the size of the problem. For only a few problems, however, have quantum algorithms been discovered which use interference effects to efficiently extract a single unambiguous result from the final superposition.

It has recently been found that macroscopic ensembles of quantum systems can use additional, albeit purely classical parallelism to accelerate the search for any desired result by a potentially large constant factor. Because incoherent averaging effects provide resilience against common forms of errors in quantum operations, such an ensemble quantum computer is also significantly easier to realize experimentally. In fact, these averaging effects can even be used to select the signals from a single quantum state out of a nearly random ensemble at thermal equilibrium. By these means it has now been possible to demonstrate all the basic principles of quantum computing by conventional liquid-state NMR spectroscopy.

There are, nonetheless, a number of practical and theoretical limits on the size of the computations which can be performed by liquid-state NMR. A more immediately practical goal may be to use NMR to simulate the dynamics of other quantum systems that are more difficult to study experimentally. This idea of simulating one quantum system by another originated with Richard Feynman, although it is implicit in older and well-established average Hamiltonian and Liouvillian techniques for designing NMR pulse-sequences. As an example of this approach, the results of experiments which simulate the first four levels of a quantum harmonic oscillator will be presented.

A simplified proof of the recent theorem of Bennett, Shor, Smolin and Thaplyal concerning entanglement-assisted classical capacity of quantum channel is presented. A basic component of the proof is a continuity property of entropy, which is established by using heavily the notion of strong typicality from classical information theory. Relation between entanglement-assisted and unassisted classical capacities of a quantum channel is discussed.

Vision and audition research in primates and humans shows two independent neural pathways; one locates objects in body-centered space, the other attributes properties, such as colour, to objects. In vision these are the dorsal and ventral pathways. In audition, similarly separable `where' and `what' pathways exist. PREDICATE

is a schematic representation of the brain's integration of the two processes of delivery by the senses of the location of an arbitrary referent object, mapped in parietal cortex, and analysis of the properties of the referent by perceptual subsystems.

The brain computes actions using a few `deictic' variables pointing to objects. Parallels exist between such non-linguistic variables and linguistic deictic devices. Indexicality and reference have linguistic and non-linguistic (e.g. visual) versions, sharing the concept of attention. The individual variables of logical formulae are interpreted as corresponding to these mental variables. In computing action, the deictic variables are linked with `semantic' information about the objects, corresponding to logical predicates.

Mental scene-descriptions are necessary for practical tasks of primates, and pre-exist language phylogenetically. The type of scene-descriptions used by non-human primates would be reused for more complex cognitive, ultimately linguistic, purposes. Thr provision by the brain's sensory/perceptual systems of about four variables for temporary assignment to objects, and the separate processes of perceptual categorization of the objects so identified, constitute a preadaptive platform on which an early system for the linguistic description of scenes developed.

In modern communication, synchronization errors arising from various physical defects in the communication links are quite common. When information-resend is not a problem, error-detection and a protocol for handling errors can take care of this. When resend is not feasible - as in high-volume traffic or deep-space communication - coding techniques that allow for the detection and correction of synchronization errors need to be employed. Error models for the type of channels used in modern communication and requirements for codes dealing with these error models need to be developed. We shall outline some of the current technical issues and present some techniques for coping with synchronization errors.

Let

be a finite set of

elements,

an integer. Suppose that

and

are pairs of disjoint

-element subsets of

(that is, $\vert A_1\vert=\vert B_1\vert=\vert A_2\vert=\vert B_2\vert=k$ , $A_1\cap B_1=\emptyset$ , $A_2\cap B_2=\emptyset$ ). Define the distance of these pairs by $d((A_1,B_1),(A_2,B_2))=\min\{\vert A_1-A_2\vert+\vert B_1-B_2\vert,\vert A_1-B_2\vert+\vert B_1-A_2\vert\}$ . One can see that this is really a distance on the space of such pairs.

denotes the maximum number of pairs

with pairwise difference at least

. The motivation comes from database theory. The lower and upper estimates use Hamiltonian type theorems, traditional code constructions and Rödl's method for packing.

cover-free family is a family of subsets of a finite set such that any intersection of

members of the family is not covered by a union of

others. A binary superimposed code is the incidence matrix of such a family. Such families also arise in cryptography as the concept of key distribution patterns. In the present paper, we develop methods of constructing such families and prove that some of them are optimal.

The generalized Dirichlet series of harmonic sum takes sometimes a meromorphic function with the residue that contains the entropy function. We will give a typical case when the entropy function appears in the residue by investigating the Bernoulli splitting process induced with biased coin. Furthermore, we can easily extend the idea of binary process to K-ary splitting process by biased dice.

S. Konstantinidis: General models of discrete channels and the properties of error-detection and error-correction

Communication of information presupposes the existence of a channel (the information medium) and a language whose words can be used to encode the information that needs to be transfered via the channel. Depending on the characteristics of the channel and the objectives of the application, the communication language satisfies certain properties such as error-correction, error-detection, low redundancy, and low encoding and decoding complexity. The classical theory of error-correcting codes [14], [15] addresses such properties. Usually, it considers probabilistic models of channels involving substitution errors and (nonprobabilistic) methods for constructing codes with error handling capabilities where error situations with low enough probability are not considered. By ignoring improbable error situations, it is also possible to consider nonprobabilistic channel models. This approach is taken, for instance, in [13],[4],[16],[1],[6],[7],[8] where channels might allow syncronization errors possibly in addition to substitution errors. It is taken implicitly in other works as well such as [3]. In this abstract we describe general models of discrete channels and define the properties of error-detection, error-correction, and unique decodability with respect to such channels. With this framework in mind, the talk might include results related to the following topics:

Informally, we use the term channel for a discrete mathematical model of a physical medium capable of carrying or storing elements that can be represented using words of a language. The medium could be anything like a computer memory, a wire, a DNA test tube, a computer typesetter, etc. In each case, the error types permitted and the way they are combined might be different and in some cases not well understood. Let

be an alphabet (e.g., $\{0,1\}$ = the binary alphabet, $\{A, C, G, T\}$ = the DNA alphabet). Then

is the set of all words over

. A language (over ) is any subset of

. A binary relation (over ) is any subset of $A^*\times A^*$ . The domain $\mathop{\rm dom}(\gamma)$ of a binary relation $\gamma$ is the set $\{w: (w,z) \in \gamma,$ for some word $z\}$ .

Definition 1 A channel $\gamma$ is a binary relation over that is domain preserving: is in $\gamma$ whenever is in $\mathop{\rm dom}(\gamma)$ . When is in $\gamma$ we say that the word can be received from via the channel $\gamma$ . If $w \not= z$ then we say that can be received from with errors.

Definition 2 A rational channel is a channel that is a rational subset of $A^*\times A^*$ ; that is, a channel realized be a finite transducer (a nondeterministic finite state machine possibly including transitions with empty input or empty output).

Rational channels include channels that are rather unreasonable in practice. They offer, however, the following advantages:

The class of SID channels allows one to model various ways of combining substitution, insertion, and deletion errors (SID errors) [6], [8]. Such channels were first considered explicitly in [13]. Here we present a subset of the full class of SID channels. An error type $\tau$ is an element of the set

$\begin{displaymath} \{\sigma, \iota, \delta, \sigma\odot\iota, \sigma\odot\delta, \iota\odot\delta, \sigma\odot\iota\odot\delta\}, \end{displaymath}$

Definition 3 The SID channel $\tau_{{\bf s}}(m,\ell)$ consists of all pairs such that can be received from using at most scattered errors of type $\tau$ in any $\ell$ consecutive symbols of . Similarly, one can define the SID channel $\tau_{{\bf b}}(m,\ell)$ with burst errors.

In [4], the contributing authors define a channel model, based on substitutions (a term for generalized homomorhisms - see below), that allows one to model various error situations. Properties of unique decodability and synchronizability for this channel model are studied in [16],[1] and [2], for instance. Let

be the source alphabet and let

be a substitution function from

into the finite subsets of

; that is, for each $s\in S$ ,

is a set of words over

that represents the possible forms of

when it is received via the channel. The fact that

is a substitution implies that $h(s_1s_2) = \{w_1w_2: w_1\in h(s_1),\, w_2\in h(s_2)\,\}$ , for every source symbols

and

. This channel model fits into the framework of Definition 1 - in this form the channels are called homophonic [7]. In fact, it is a special case of the rational channel model.

Let $\gamma$ be a channel. A language

is error-detecting for $\gamma$ , [11], if $(w_1,w_2)\in\gamma$ implies

for all words $w_1,w_2\in L_{\lambda}$ , where $L_{\lambda}=L\cup\{{\lambda}\}$ and ${\lambda}$ is the empty word. Assuming that only words from $L_{{\lambda}}$ are sent into the channel, if

is retrieved from the channel and

is in $L_{\lambda}$ then

must be correct; that is, equal to the word that was sent into the channel. On the other hand, if the word retrieved from the channel is not in $L_{\lambda}$ then an error is detected. The use of $L_{{\lambda}}$ as opposed to

ensures that ${\lambda}$ cannot be received from a word in $L\setminus\{{\lambda}\}$ and that no word in $L\setminus\{{\lambda}\}$ can be received from ${\lambda}$ . Of particular interest is the case where the language

is coded; that is,

for some (uniquely decodable) code

. In this case, it is possible to define the concept of error-detection with finite delay [11], [12].

A language

is error-correcting for the channel $\gamma$ , [10], if $(w_1,z),(w_2,z)\in\gamma$ implies that

for all words $z\in X^*$ and $w_1,w_2\in L_{{\lambda}}$ , where $L_{{\lambda}}=L\cup\{{\lambda}\}$ . Assuming that only words from $L_{{\lambda}}$ are sent into the channel, if

is retrieved from the channel then there is exactly one word from $L_{{\lambda}}$ that has resulted in

. Therefore, even if

has been received with errors then, in principle, one can find the word $w\in L_{{\lambda}}$ with $(w,z)\in\gamma$ , correcting thus the errors in

. In the definition, the use of $L_{{\lambda}}$ ensures that the empty word and a nonempty word of

can never result in the same output through the channel $\gamma$ . It should be clear that if a language is error-correcting for $\gamma$ then it is also error-detecting for $\gamma$ , assuming that the language is included in the domain of the channel $\gamma$ . A code

is uniquely decodable for the channel $\gamma$ (or $(\gamma,*)$ -correcting [7]) if the language

is error-correcting for $\gamma$ .

E.V. Konstantinova: Applications of information theory in chemical graph theory

Information theory has been used in various branches of science. During recent years it is applied extensively in chemical graph theory of describing chemical structures and for proving good correlations between physico-chemical and structural properties. In this talk we survey the old and new results concerning information theory applications to characterizing molecular structures. The Shannon formula is used for constructing information topological indices. These indices are investigated with respect to their basic characteristics that are the correlating ability with a molecular property and the discrimination power.

V. Levenshtein: Combinatorial and Probabilistic Problems of Sequence Reconstruction

New problems of reconstruction of an unknown sequence of a fixed length with the help of the minimum number of its patterns which are distorted by errors of a given type are considered. These problems are completely solved for combinatorial channels with substitutions, permutations, deletions, and insertions of symbols. Asymptotically tight solution is also found for a discrete memoryless channel and for the continuous channel with discrete time and additive Gaussian noise.

T. Berger and V. Levenshtein: Coding Theory and Two-Stage Testing Algorithms

The problem of finding optimal linear codes and of constructing optimal two-stage tests are connected through the need to find an optimum parity check matrix and an optimum test design matrix, respectively. The efficiency of two stage testing of n items which are active or not according to a Bernoulli distribution with parameter

is characterized by the minimum expected number

of disjunctive tests, where the minimum is taken over all test matrices used in the first stage. We use coding theory methods to obtain new upper and lower bounds which determine the asymptotic behavior of

up to a constant factor as

tends to infinity and

tends to

M. Blaeser, A. Jakoby, M. Liskiewicz, and B. Siebert: Private Computations on -Connected Communication Networks

We study the role of connectivity of communication network in private computations under information theoretic settings. In a talk a general technique will be shown for a simulation of private protocols on any communication network by private protocols on an arbitrary

-connected network which use for this simulation only a small number of additional random bits. Furthermore, it will be proved that some non-trivial functions can be computed privately even if the used network is

-connected but not

-connected and finally, a sharp lower bound will be given for the number of random bits needed to compute some concrete functions on all

-connected networks.

K. Mainzer: Information Dynamics in Nature and Society. An Interdisciplinary Approach

In the age of information society, concepts of information are an interdisciplinary challenge of mathematics and computer science, natural and social sciences, and last but not least humanities. The reason is that the evolution of nature and mankind can be considered as an evolution of information systems. On the background of the theories on information, computability, and nonlinear dynamics, we suggest a unified concept of information, in order to study the flow of information in complex dynamical systems from atomic, molecular and cellular systems to brains and populations. During the past few years, natural evolution has become a blue-print for the technical development of information systems from quantum and molecular computing to bio- and neurocomputing. Mankind is growing together with the information and communication systems of global networking. Their information flow has remarkable analogies with the nonlinear dynamics of traffic flows. Net- and information chaos needs new methods of information retrieval. In the age of globalization, our understanding and managing of information flows in complex systems is one of the most urgent challenges towards a sustainable future of information society.

M.B. Malyutov: Non-Parametric Search for Significant Inputs of Unknown System

Suppose we can measure the output of a system whose input is a binary

-tuple

. It is known that the output (which may have a continuous distribution) depends only on an

-tuple

of the inputs labeled by a subset

of $\{ 1,...,t\}$ with $\vert S\vert=s<t$ .

is equally likely, a priori, to be any

-subset of

inputs. Fixing inputs in

trials (design) we observe outputs which are conditionally independent given design. The choice of analysis of outputs and design to minimize the number

of trials for finding the set

under a prescribed upper bound

for error probability is studied. This problem turns out to be closely related to that of studying optimal transmission rate for multiple access channels (MAC) with or without feedback. Asymptotic bounds for

under small

and/or large

are found. The cases of fixed and increasing

, sequential and non-sequential design are studied. A universal asymptotically optimal nonparametric analysis of outputs applicable without any knowledge of the system based on maximization of Shannon Information between some classes of input-output empirical distributions is studied.

Whereas information theory has been very successful in characterizing the technical aspects of information transfer over channels without feedback, it has been much less successful in dealing with channels with feedback. Shannon himself in 1973 seemed to suggest that feedback communications needed rethinking by information theorists. Some reasons for this failure of information theory will be proposed. Some possible approaches to theory of feedback communications based on directed information and causally conditioned directed information will be discussed.

I will present a survey on recent results concerning pseudorandomness of finite binary sequences. In a series of papers, A. Sárközy and myself introduced new measures of pseudorandomness connected to the regularity of the distribution relative to arithmetic progressions and the correlations. We analysed and compared several constructions including the Legendre symbol, the Thue-Morse sequence, the Rudin-Shapiro sequence, the Champernowne sequence, the Liouville function (jointly with J. Cassaigne, S. Ferenczi and J. Rivat), and a further construction due to P. Erdos related to a diophantine approximation problem. We also study the expectation and the minima of these measures and the connection between correlations of different order.

M. Loewe, F. Merkl, and Silke Rolles: Moderate deviations for longest increasing subsequences in random permutations

The distribution of the lengths of longest increasing subsequences in random permutations has attracted much attention especially in the last five years. In 1999, Baik, Deift, and Johansson determined the (nonstandard) central limit behaviour of these random lengths. They use deep methods from complex analysis and integrable systems, especially noncommutative Riemann Hilbert theory. The large deviation behaviour of the same random variables was determined before by Seppaelaeinen, Deuschel, and Zeitouni, using more classical large deviation techniques. In the talk, some recent results on the moderate deviations of the length of longest increasing subsequences are presented. This concerns the domain between the central limit regime and the large deviation regime. The proof is based on a Gaussian saddle point approximation around the stationary points of the transition function matrix elements of a certain noncommutative Riemann Hilbert problem of rank 2.

V.N. Koshelev and E.C. van der Meulen: On the duality between successive refinement of information by source coding with fidelity constraints and efficient multi-level channel coding under cost constraints

Shannon (1959) pointed out a certain duality between (one-step) source coding with a fidelity criterion on the one hand, and (one-step) coding for a memoryless input-constrained channel on the other. Mathematically, this duality is reflected by two main informationtheoretical quantities known as the rate-distortion function and the capacity-cost function, respectively. Shannon (1959) proved coding theorems showing that the rate-distortion function R(D) can be achieved for average distortion D in the source coding problem, and that the capacity-cost function C(t) can be achieved if the average cost per channel input is at most t in the channel coding problem.

Koshelev (1980) introduced the concept of hierarchical source coding, and provided a sufficient condition for so-called successive refinement (or source divisibility). Equitz and Cover (1991) proved the necessity of this condition. This condition is that the individual solutions of the rate-distortion problems can be written as a Markov chain.

In this presentation we consider multi-level channel coding subject to a sequence of input constraints, and formulate the notion of efficient successive two-level channel coding. We prove sufficient conditions for efficient successive channel coding subject to two cost constraints (channel divisibility). These conditions also involve a Markov-relationship, namely between the individual solutions of the respective capacity-cost problems.

This talk surveys strategies for distributing and accessing shared objects in large parallel and distributed systems. Examples for such objects are, e.g., global variables in a parallel program, pages or cache lines in a virtual shared memory system, or shared files in a distributed system, for example in a distributed data server. I focus on strategies for distributing, accessing, and (consistently) updating such objects, which are provably efficient with respect to various cost measures. First I will give some insight into methods to minimize contention at the memory modules, based on redundant hashing strategies. This is of interest for, e.g., the design of real time storage networks, as we develop within our PReSto-project in Paderborn. The main focus of this talk is on presenting strategies that are tailored to situations where the bandwidth of the network (rather than the contention at the mamory modules) is the bottleneck, so the aim is to organise the shared objects in such a way that congestion is minimized. First I present schemes that are efficient w.r.t. information about read- and write-frequencies. The main part of the talk will deal with online, dynamic, redundant data management strategies that have good competitive ratio, i.e., that are efficient compared to an optimal dynamic offline strategy that is constructed using full knowledge about the dynamic access pattern. Especially the case of memory restrictions in the processors will be discussed.

A. Miklosi: Some general insights of animal communication from studying interspecific communication

There are two extrem cases in animal (including human) communication. At one extreme animal communication can be viewed as a behavioral regulatory mechanism between conspecifics. Such communication can be witnessed in agressive contest or takes place during courtship. In this case, communicative signals are part of a closed behaviour systems where the ``information content'' of such signalling is limited. The other extreme of forms of communication is a means to modify the mental content of another individual by using various forms of referential signalling. These systems are characterised of their openness and learning plays also some part in both production and comprehension of communicative signals. Assuming that brains represent mental models of the environment the main question is how signals that are being the product of one mental model can influence the representations in the other. Within a species it can be assumed that mental models are correspondingly similar to each other and therefore signals will have the same effect in the case of each individuals. If a signal plays the same role in the mental models of both communication individual, we might talk of 100considering the case of interspecific communication correspondence can be much lower. In the dog's mental model of the environment the call ``Come here!' represent a very different component compared of that it plays in the mental modell of a human hearing the same utterance. There are two ways of increasing correspondence in interspecific communication. If there is time avaiable genetic changes could contribute to changes in the communicative systems in both species that increase correspondance. In the other, not exclusive case individuals of both species should engage in learning to increase correspondence. In turn this assumes also some flexibility in both comprehension and production of communicative signals. Species with more relaxed motor patterns and less selective recognition systems have an advatages here. In my overview of this topic I will illustrate this by using the naturally occuring communicative behaviour of honeyeater birds and humans, differences and similarities of human-dog and human-ape communication.

F. Cicalese and D. Mundici: Learning, and the art of fault-tolerant guesswork

Fix two positive integers

and

. The smallest integer

such that $2^q \geq M(1+q+{q \choose 2}+\ldots+ {q \choose e})$ is known as the Berlekamp sphere-packing bound, and is denoted

. In binary search it is impossible to find an element $x \in \{1,\ldots,M\}$ using less than

tests, up to

of which may be faulty. On the other hand, using (a minimum of) adaptiveness, for most

and

such

can be found using exactly

tests. Whether the same optimality result holds when no adaptiveness is allowed is a basic problem for

-error correcting codes, for which only fragmentary, usually negative, answers are known. The lower bound

for

-fault tolerant binary search turns out to be an upper bound for the number of wrong guesses in several learning and online prediction models. In most cases, the bound is tight.

Irene Pepperberg: Lessons from Cognitive Ethology: Models for an Intelligent Learning/Communication System

Computers may be 'smart' in terms of brute processing power, but their abilities to learn are limited to what can easily be programmed. Computers presently are analogous to living systems trained in conditioned stimulus-response paradigms. Thus, a computer can solve new problems only if they are very similar to those it has already been programmed to solve. Computers cannot yet form new abstract representations, manipulate these representations, and integrate disparate knowledge (e.g., linguistic, contextual, emotional) to solve novel problems in ways managed by every normal young child. Even the Grey parrots I study, with brains the size of a walnut, succeed on such tasks. Such success likely arises because a parrot, like a young child, has repertoire of desires and purposes that cause it to form and test ideas about the world and how it can deal with the world; these ideas, unlike conditioned stimulus responses, can amount to representations of cognitive processing. I suggest that by deepening our understanding of the processes whereby nonhumans advance from conditioned responses to representation-based learning, we will begin to uncover rules that can be adapted to nonliving computational systems.

The asymptotic behavior of the epsilon-entropy of ellipsoids in the Hamming space is investigated as the dimension of the space grows.

This talk gives an overview on algorithmic issues concerning probability distributions and information transfer that have to be taken into account for efficient realizations. From a computational complexity perspective we introduce issues like Algorithmic Learning, Data Mining, Communication Complexity and Interactive Proof systems.

Computationally hard problems, for which there is little hope for an eficient solution by standard deterministic algorithms, can be attacked by heuristics or in a more analytical way using parallelism, randomness, approximation techniques, and by considering the average-case behaviour.

We concentrate on average-case analysis discussing appropriate average-case measures. Since there exists a non-computable universal distribution that makes the average-case complexity as bad as the worst-case one has to think about what are reasonable or typical distributions for a computational problem and how one could measure the complexity of distributions themselves. These questions are illustrated for the sorting problem, for graph problems when the random graph model is used, and for the satisfiability of Boolean formulas. Further issues like reductions between distributions have to be dealt with that lead to notions like polynomial dominance and equivalence between distributions. As an example, we discuss the delay in Boolean circuits as a suitable such average-case measure.

Finally, we present a generalisation of the information transmission problem that models discrete problems in a situation where the assumption of fault-free input data is no longer realistic, for example in fields like Molecular Biology. Even then one would like to solve optimization problems with a similar efficiency as in the case without errors. Our goal is to identify cases where such a hope may be realistic, and then to find appropriate algorithmic methods.

We give an overview on the analysis of algorithms and machines with respect to their average-case behaviour. For the worst-case there is a well established framework to measure the efficiency of algorithms that yields a robust classification of the complexity of algorithmic problems. With respect to the every case, things are more subtle.

We discuss suitable average-case measures for different computational models that do not destroy reduction properties and polynomial time equivalence. For nonuniform distributions the algorithmic complexity of the distribution itself turns out to be of importance as well.

We illustrate this approach by considering the delay of Boolean circuits. For certain basic functions one obtaines an exponential speedup in the average case compared to the worst case.

Algorithmic Learning deals with the following problem. For a given learning domain (for example, the set of all binary vectors of some fixed length) one has to learn a subset called a concept. The unknown concept is chosen from a given concept class, a subset of the powerset of the learning domain. The learner gets a sequence of examples from the concept. After each example he has to provide a hypothesis what the concept might be. One likes to minimize the number of wrong guesses and the total amount of work till the learning procedure has converged to a correct hypothesis. Obviously, the effort depends on the concept to be learned and the concept class, but also on the sequence of examples given to the learner.

Several versions of this problem have been studied. Inductive Inference considers learning in the limit, where it is assumed that the sequence of examples is chosen by an adversary, but eventually this sequence has to contain all members of the concept. In Valiant's PAC-model, (probably approximately correct) the examples are drawn according to an unknown distribution on the learning domain. Now it is only required to compute an approximation of the concept which should be close to the true concept with high probability according to the underlying distribution.

The talk discusses a new model called stochastic finite learning introduced by Zeugmann and the author recently. We study the average case complexity of learning for natural classes of distributions and illustrate the problem of learning monomials and pattern languages. Very efficient algorithms can be obtained in the 1-variable case implying that worst case bounds obtained for limit learning and PAC learning based on the VC dimension are too pessimistic.

Z. Reznikova and B. Ryabko: Use ideas of Information Theory to study animal communication: a new tool to find news

The ability of language behaviour in animals is one of the best manifestations of intelligence closely related to their social life. Although it is intuitively clear that many high social species have to possess complex language, only two types of natural communications have been decoded, namely the intricate ``Dance Language'' of eusocial insects ( honey bee) and acoustic signals of vervet monkeys and of several other species. The main difficulties in the analysis of animal language appear to be methodological. Many workers have tried to directly decode animal language by looking for ``letters'' and ``words''. The fact that ``dictionaries'' were compiled for a few species only, appears to indicate not that other animals lack language, but that adequate methods are lacking. It is natural to use ideas of Information Theory in investigation of natural languages, because this theory presents general principles and methods for developing effective and reliable communicative systems. The main point of our approach is not to decipher signals but to investigate just the process of information transmission by measuring time duration which the animals spend on transmitting messages of definite lengths and complexities. Basing on these ideas, we recently have revealed sophisticated communication system and numerical competence in several highly social ant species ( see Complexity, 1996, 2,2: 37-42; From Animals to Animats 6, The MIT Press, 2001: 501-506). These eusocial animals were demonstrated as being able to transmit a definite amount of information to each other in order to obtain food, use simple regularities for information coding and small numbers for coding coordinates of objects. It is a great challenge to extend these experimental schemes and approaches for studying evolution of communication within wide variety of species.

We will present different classical notions of pseudorandomness and introduce the measures of Mauduit and Sárközy. We will show that these measures permit to handle some classical tests. Then we will present a construction based on the Legendre symbol (the Q-construction), discuss its possible use in cryptography and present some numerical data.

The problem of predicting a sequence

where each

belongs to a finite alphabet

is considered. Each letter $x_{t+1}$ is predicted using information on the word

only. We use the game theoretical interpretation which can be traced to Laplace where there exists a gambler who tries to estimate probabilities for the letter $x_{t+1}$ in order to maximize his capital. The optimal method of prediction is described for the case when the sequence

is generated by a stationary and ergodic source. It turns out that the optimal method is based only on estimations of conditional probabilities. In particular, it means that if we work in the framework of the ergodic and stationary source model, we cannot consider pattern recognition and other complex and interesting tools, because even the optimal method does not need them. That is why we suggest a so-called nonprobabilistic approach which is not based on the stationary and ergodic source model and show that complex algorithms of prediction can be considered in the framework of this approach. The new approach is to consider a set of all infinite sequences (over a given finite alphabet) and estimate the size of sets of predictable sequences with the help of the Hausdorff dimension. This approach enables us first, to show that there exist large sets of well predictable sequences which have zero measure for each stationary and ergodic measure. (In fact, it means that such sets are invisible in the framework of the ergodic and stationary source model and shows the necessity of the new approach.) Second, it is shown that there exist quite large sets of such sequences that can be predicted well by complex algorithms which use not only estimations of conditional probabilities.

Mauduit and Sárközy defined the concept of pseudorandomness of finite binary sequences as good distribution relative to arithmetic progressions and small correlations (including both higher order and long range correlations). 4 different constructions of finite binary sequences with good pseudorandom properties are presented. The first one uses the Legendre symbol and polynomials, the second one the concept of index (or ``discrete logarithm''), the third additive characters and polynomials; in each of the three cases the proof is based on a theorem of Weil. The fourth construction uses elliptic curves but only computational evidences are obtained.

K. Smith: Compositionality from culture: the role of environment structure and learning bias

Human language is unique among the communication systems of the natural world - it is a learned, symbolic communication system which exhibits compositional structure. Compositional communication systems reflect the structure of underlying mental representations or communicative intentions in the structure of externalised signals. They can be contrasted with holistic communication systems, where signals are unstructured or their structure does not reflect structured mental representations. How did human language come to be compositional?

Pinker & Bloom (1990) and Nowak et al. (2000) argue that structured language emerged due to natural selection for a biological capacity to acquire syntactic communication systems. Others suggest that compositionality could have arisen through purely cultural processes in a genetically-homogeneous community. The models presented in Kirby (2000) and Brighton (2002) show that compositional communication systems can emerge through cultural evolution.

A new dynamic model of the cultural evolution of compositionality is introduced. This model is an iterated learning model - the output of learning at one generation forms the input to learning at the next generation. This model both confirms the results produced by earlier iterated learning models and gives new insights into the cultural evolution of communication.

Firstly, the model shows that compositional systems are more likely to emerge when the environment exhibits a high degree of structure. Secondly, the learning biases required to construct a compositional system from a random system through purely cultural processes can be shown to be a wlll-defined subset of those learning biases identified in Smith (2002) as sufficient to construct an optimal holistic communication system. This suggests that any transition from holistic to compositional communication could occur without any change in a population's biologically-specified learning mechanism.

Perception of environmental structure and an appropriate learning bias form preconditions for the cultural evolution of compositional communication. We can hypothesize that humans or a recent predecessor were unique in meeting these preconditions.

Some results on perfect codes obtained during last 6 years are discussed. The main methods to construct perfect codes such as method of $\alpha$ -components and concatenation approach and their implementations to get decisions of some important problems are analyzed. The decision of rank-kernel problem, the lower and upper bound of the automorphism group order of a perfect code, spectral properties, isometries of perfect codes and codes close to them by close-packed properties are considered.

$\begin{displaymath} A_n=\left(\begin{matrix} c_0&c_1&c_2&\dots&c_{n-1}\\ c_1&c_... ...vdots\\ c_{n-1}&c_n&c_{n+1}&\dots&c_{2n-2}\end{matrix}\right).\end{displaymath}$

In Combinatorial Theory one is interested in identities arising from determinants of Hankel matrices of a given sequence $c_0,c_1,c_2,\dots$ . For instance, Hankel matrices consisting of Catalan numbers have been analyzed by various authors. Desainte-Catherine and Viennot found their determinant to be $\prod_{1\leq i\leq j\leq k}\frac{i+j+2n}{i+j}$ . We can further show that determinants of Hankel matrices consisting of numbers $\frac1{3m+1}\binom{3m+1}m$ yield an alternate expression of a formula important in the enumeration of alternating sign matrices.

In Coding Theory, Hankel matrices arise, where the entries

are syndromes resulting after the transmission of a code word encoded with a BCH-code. The famous Berlekamp-Massey algorithm usually is used for decoding. The well-known relation of Hankel matrices to orthogonal polynomials now yields a combinatorial application of the Berlekamp-Massey algorithm, namely the calculation of the coefficient in the three-term recurrence of the family of orthogonal polynomials related to the sequence of Hankel matrices.

J. Tautz: A biologists view of communication: its strengths and its needs for interdisciplinary approaches

If a signal sent by one animal is followed by a response in another animal, communcation has happened. In studying and finally understanding animal communication the broadest approach one can imagine has to be adopted. A genuine biological view is that on the evolution of communication systems. Investigating a range of species guided by a phylogenetic frame leads to deep insights into options and limits in the evolution of communication systems. Communication biology can trigger directions of research in related fields, as it can gain a lot from ideas and approaches from outside biology.

In communication biology first the mechanisms of communication are investigated: A careful micro-behavioral analysis, the recording and analysis of all signals detectable and the study of the signal-transmission channel gives the relevant details. In a next step the economics of communication are being studied, i.e. the costs and benefits of sending and receiving signals. In the last step the conflicts of interests between senders and receivers are being studied in order to understand better systems which on first sight are less than optimal constructed.

In a personal view I see problems in the application of quantitaive parameters describing information and communication developed for technical systems. It is straightforward to calculate measures for communication systems for which the mechanisms are understood. But to what extend are they biologically meaningful? Which technical terms can be meaningfully applied to steps two and three (see above) in the analysis of biological communication systems?

In a cooperation between mathematicians, theoretical communication scientists and biologists it should be evaluated, to which extend the application of technical terms to biological communication systems are useful. If the answer would not be satisfying, the development of alternative parameters to describe, to measure or to calculate key aspects of information and communication may open new aspects for biology as well as technical fields.
The ``dance language'' in honeybees will be used in the talk to exemplify some of the aspects mentioned above.

We discuss coding for a channel producing errors where a side-channel possibly informs the decoder about part of the information that is encoded in the transmitted codeword. The encoder does not know about which part of the information, in any, the decoder will be informed. The aim is the design of codes and encoders for which knowledge of some information symbols enhances the error-correcting capabilities.

The motivation for this research was address retrieval on optical media. In this application, we aim to let the reading or writing head in a target sector t with address a (t) and know it will land close to t. In order that informed decoding can be applied, a (s) should agree with a (t) in a large set I (t) of positions whenever s and t are close to each other. We show some initial results on how to choose the address mapping a.

A.G. D'yachkov and P.A. Vilenkin: On a Class of Codes for the Insertion-Deletion Metric

We study the problems of combinatorial coding theory connected with a class of

-ary codes for the insertion - deletion distance function [1] in the space of

-ary

-sequences. The codes are called reverse - complement codes (RC codes) for the insertion - deletion metric (ID metric). Quaternary (

) RC codes for ID metric arise from the potentialities of molecular biology [2]. With the help of random coding arguments we obtain a lower bound on the code rate. The bound can be also applied to the rate of conventional insertion - deletion correcting codes [1] and, hence, our result is an advance in the combinatorial coding theory, where only for

an essentially weaker lower bound on the rate is known [3].

E. Wascher: An integrative approach to human information processing: From Pawlows dog to functional imaging

In the first half of the 20th century, psychology was determined by behaviourism. In trying to create an objective psychology it was intended to exclude introspective approaches to human mind. Behaviourism was based on a pure description of observable, repeatable behaviour. The main thesis was that humans being adapted to their environment using the tools provided by their genetic and learning history. John B. Watson believed that the response of an organism to any given stimulus can be accurately predicted. According to this view, human behaviour would be nothing but responding to external stimulation.

In the 1950ies, psychology left the position of behaviourism. Psychology at these days was strongly influenced by the first computers. Following the computer metaphor, human behaviour was defined as the result of symbol-based encoding, performance of operations on, and output transmission of informational input. Information processing was assumed to occur in discrete substages, comparable to mechanisms taking place in electronic machines.

From a todays point of view this position suffers from two major shortcomings: (1) The neural system is too slow and too inaccurate to process information that way, and (2) mental representations cannot be excluded from human information processing just because they appear not to be objectively measurable.

Recent research on the functional properties of neural cell populations provide a new sight on human information processing. The integration of information within assemblies of neurons compensate the temporal deficit of single neuron information transmission. Additionally, there is increasing evidence that both aware and unaware processing of information play a particular role in preparing and selecting appropriate actions. Distinct cortical pathways are processing these two types of information. The motor system can integrate aware and unaware information depending on the task. Thereby, the border between visuo-motor (unaware) and cognitive (aware) information transmission is rather fuzzy. Minimal changes of a task might change the way information is processed in a system that is always trying to be as efficient as possible.

The lecture is about a special type of Combinatorial Search, the so called recognition problem.

In the classical model of Combinatorial Search a ground set

and a set system $\cal A$ on

are given, and our aim is to find a hidden element $x\in H$ with as few questions of type ``is $x\in A$ ?'' as possible, where

must be a member of $\cal A$ . This may be called an identification problem.

Now let furthermore a function $f: H\to\{0, 1\}$ be given; now our aim is to compute the value

, instead of finding

itself. This is called a recognition problem, because we have to verify if the hidden element is a member of the set $\{x: f (x) = 1\}$ or not.

We shall survey the recognition problem itself and some interesting special cases as well.

From humble beginnings, Schumacher's quantum version of the well-known Shannon data compression of statistical sources, which itself is a cornerstone of the emerging field of quantum information theory, establishing the von Neumann entropy as an operationally founded information measure, our understanding of quantum data compression has dramatically increased since 1994, both in its relation as well as its opposition to the classical theory.

The talk will review the `state of the art' in this field, whose results amply demonstrate the peculiarities of quantum information: generically, quantum resources cannot be saved by allowing extraction of classical information from the source (reporting joint work with Barnum, Hayden and Jozsa), and in a ``visible source'' scenario, we know now the exact trade-off between classical and quantum bits (joint work with Hayden and Jozsa), implying insights into other questions of quantum information theory.

Also, in universal compression, great advances have been made: this problem has its own quantum flavour, as the usual strategies of estimating the parameters of the source by observation run into difficulties due to the fact that generally measurements introduce irrecoverable disturbances on the quantum data. If time allows, I will explain the very recent i.i.d.-universal quantum source coding scheme of Matsumoto and Hayashi.

Since the advent of general relativity theory, the strive for a unification of science has entered a new phase of intensity. For Einstein himself, it appeared appropriate to look for a unification in terms of gravitation and electromagnetism, the two fundamental forces at the time. To be more precise: His idea was to actually include electromagnetic fields in his gravitational field equations by introducing them into the metric components of space-time, in the first place. The subsequent advent of quantum theory however, to which Einstein himself contributed fundamental insight, led to a much more complex situation, because not only did two more forms of interaction (weak and strong fields) turn up, but the basic interpretations of relativity on the one side and quantum theory on the other, differed according to their respective (worldly) domains: on the one hand, relativity being defined in terms of a four-dimensional space-time manifold with a Lorentz metric (of signature -2), quantum theory on the other, showing up in terms of a high-dimensional Hilbert manifold with a positive-definite (Euclidean) metric. Hence, one ended up with two disjoint domains claiming to explain the same universe. During the last three decades, a basically different approach to unification has been put forward going back to an old idea of John Wheelers: If it is not possible to unify the competitors within the world, it might be possible to unify them outside the world, the basic idea being to introduce an abstract mathematical structure from which space and time (and matter) as fundamental categories of the world could be eventually derived. Hence, the idea is to visualize the world as a variety which has become out of a primordial (actually pre-worldly) unity. If so, then the next step, namely to formulate this the other way round: that the world is in fact this primordial unity as being observed as a becoming variety by its members who have restricted means of perception, is relatively small. The question is how to reasonably approach such a conception in more detail. Because, technically, this would point to achieving a unified context for both gravitation and quantum theory anyway. A useful motivation for quantum gravity of that sort has been given by John Baez recently¹: There are three fundamental length scales, defined in terms of three physical constants coming from both regions in question (h, the Planck constant divided by 2p, Newtons gravitational constant G, and the velocity of light c, respectively), which are important for relativity and quantum theory, at the same time. One is the Planck length lP = (hG/c3)1/2, of roughly the order of magnitude of 10-35 m. For length scales smaller than this, quantum gravity would be the appropriate tool to describe the physics there. Another one is the Compton wavelength, lC = h/mc, which basically indicates that the measuring of the position of a particle of mass m precisely within one Compton length, requires energy which is able to create another particle of the same mass. Hence, this length scale is characteristic for effects in quantum field theory. Finally, there is the Schwarzschild radius which basically defines the horizon of a black hole which has been formed by a collpasing star of mass m: lS = Gm/c2. (All constants up to numerical factors.) If m is now the Planck mass itself (mP = (hc/G)1/2), then lC = lS = lP. Hence, we would suppose that at the Planck scale, both domains of physics should show up in a somewhat unified way. It is quite natural to ask then, whether the continuum picture of space-time is only an approximation which inevitably breaks down when approaching the Planck scale. And if so, whether there are constituents of space and time which show up according to some scheme of quantization, such as to construct quantum operators with discrete eigen-values. The microscopic structure of space and time would be determined then by eigenvalues and eigenvectors of purely geometric operators, and the macroscopic superposition of these would show up as the well-known space-time continuum (as a limit for large values). But this would also mean to abandon any underlying space-time structure we have got accustomed with. As Ashtekar and Krasnov have pointed out, ... to probe the nature of quantum geometry, one should not begin by assuming the validity of the continuum picture; the quantum theory itself has to tell us, if the picture is adequate ...² For their approach, referred to as loop quantum gravity, it is the goal therefore, to find a background-free quantum theory with local degrees of freedom propagating causally. Essentially, Ashtekar and Krasnov refer back to Wheelers conception, in actually introducing a split of space and time: Hence, their dynamics is essentially one of 3-dimensional Riemannian spaces, only, and the full dynamical content of general relativity is captured by three constraints of this ansatz that generate the appropriate gauge invariances (under local SU(2) gauge transformations, three-dimensional diffeomorphisms, and coordinate time translations generated by the Hamiltonian constraint). ³ So what we can do now is to compare the configuration variable of general relativity as known from gauge theories with the SU(2) connection A on a spatial 3-manifold, and the canonically conjugate momentum E with the Yang-Mills electric field. Physically, the latter is essentially the triad and carries all information about space. This is where in quantum theory, the gauge invariant Wilson loop functionals are coming in: They are the path-ordered exponentials of the connections around closed loops. Hence, the name for the theory (loop quantum gravity). Usually, the kinematics of quantum theory is defined by an algebra of operators on a Hilbert space. The outcome of the physical theory will depend on the connection which can be uncovered between operators and classical variables, and on the interpretation of the Hilbert space as a space of quantum states. The dynamics is determined by a Hamiltonian constructed from the operators. The idea is now to express quantum states in terms of the amplitude of the connection, given by some functional of the type Y(A) in the sense of Schrödinger. Functionals of this kind form a space which can be made into a Hilbert space provided a suitable inner product is being defined. Having done this, we can express the amplitude as Y(A) = <AôY> in Dirac notation. Is now H our Hilbert space, then we define H0 as its subspace formed by states invariant under SU(2) gauge transformations. Then it can be shown that an orthonormal basis in H0 is actually a spin network basis. Basically, spin networks are graphs with three-valued nodes and spin values on the edges, their states being denoted by ½G>. To take the norm refer to the mirror image of a graph and tie up the ends, forming a closed spin network $G\char93 G^*$ of value V such that <G½G> = $V(G\char93 G^*)$ with V(...) = P (1/j!) S e(-2)N, here j being the edge label, N the number of closed loops, and e referring to the intertwining operation taking care of permutations of signs. The product is to be taken over all edges, the sum over all routings. Hence, the networks can be visualized in diagrammatic form such as to represent the underlying spin dynamics. Spin interactions of this kind can lead to the creation of new structures: Take a large part of the network and detach from this small m-units, and n-units, respectively, as free ends. The outcome of their tying up to form a new structure can be estimated in terms of a probability for the latter having spin number P, say. This turns out as being basically the quotient of the norm of the closed network and the norm of the network with free ends (times some intertwining operations). The spin geometry theorem tells us then that when repeating this procedure and getting the same outcome, then the new quotient is proportional to (1/2) cos q, where the angle is one which is taken between the axes of the large units. Hence, it is possible to show that angles obtained in this way satisfy the well-known laws of Euclidean geometry. Or, in other words: This purely combinatorial procedure can be used to actually approximate space from a pre-spatial structure which is more basic. This idea has been due to Penrose who originally tried to base his concept of twistors on spin networks.⁴ The consequences of this approach have remained relevant until today, while a generalization of spin networks and a connection with knot theory has been achieved more recently by Carlo Rovelli and Lee Smolin referring to loop quantum gravity: They start with loops from the outset and show that since spin network states <S÷ span the loop state space, it follows that any ket state ÷y> is uniquely determined by the values of the S-functionals on it, namely of the form y(S) := <S½y>. To be more precise, Rovelli and Smolin take embedded spin networks rather than the usual spin networks, i.e. they take the latter plus an immersion of its graph into a 3-manifold. Considering then, the equivalence classes of embedded oriented spin networks under diffeomorphisms, it can be shown that they are to be identified by the knotting properties of the embedded graph forming the network and by its colouring (which is the labelling of its links with positive integers referring to spin numbers). ⁵ When generalizing this concept even further, a network design may be introduced as a conceptual approach towards pre-geometry based on the elementary concept of distinctions, as Louis Kauffman has shown. ⁶ In particular, space-time can be visualized as being produced directly from the operator algebra of a distinction. If thinking of distinctions in terms of 1-0 (or yes-no) decisions, we have a direct link here to information theory, which has been discussed recently again with a view to holography. ⁷Ashtekar and Krasnov have noted this already when deriving the celebrated Bekenstein-Hawking formula in applying loops to black holes. Referring to punctured horizons they can show that each set of punctures gives actually rise to a Hilbert space of (Chern-Simons) quantum states of the connection on the horizon. Be P = jp1 ... jpn the set of punctures, and Hp the respective Hilbert space. Then dim Hp PjpÎP(2jp + 1), and the entropy of the black hole is simply given by Sbh = ln åP dim HP. The edges of spin networks can be visualized then as flux lines carrying area. With each given configuration of flux lines, there is a finite-dimensional Hilbert space describing the quantum states associated with curvature excitations initiated by the punctures of the horizon. Because the states that dominate the counting (for S) correspond to punctures all of which have labels j = ½, each microstate can be thought of as providing a yes-no decision or an elementary bit of information. ⁸ Hence, the reference to Wheelers It from Bit. (Paola Zizzi has tried to generalize this within the conception of inflationary cosmology, and terms this It from Qubit.) Note that according to the standard terminology, a loop in some space S, say, is a continuous map g from the unit interval into S such that g(0) = g(1). The set of all such maps will be denoted by WS, the loop space of S. Given a loop element g, and a space A of connections, we can define a complex function on A x WS, the socalled Wilson loop such that TA(g) := (1/N) TrR P exp òg A. Here, the path-ordered exponential of the connection AÎA, along the loop g, is also known as the holonomy of A along g. The holonomy measures the change undergone by an internal vector when parallel transported along g. The trace is taken in the representation R of G (which is actually the Lie group of Yang-Mills theory), N being the dimensionality of this representation. The quantity measures therefore the curvature (or field strength) in a gauge-invariant way.⁹ Over a given loop g, the expectation value < T(g)> turns out to be equal to a knot invariant (the Kauffman bracket) such that when applied to spin networks, the latter shows up as a deformation of Penroses value V(G). Hence, spin networks are deformed into quantum spin networks (which are essentially given by a family of deformations of the original networks of Penrose). There is also a simplicial aspect to this: Loop quantum gravity provides for a quantization of geometric entities such as area and volume. The main sequence of the spectrum of area e.g., shows up as A = 8pghG åi(ji(ji + 1))1/2, where the js are half-integers labelling the eigenvalues. (Compare this with the remarks on black holes above.) This quantization shows that the states of the spin network basis are eigenvalues of some area and volume operators. We can say that a spin network carries quanta of area along its links, and quanta of volume at its nodes. A quantum space-time can be decomposed therefore, in a basis of states visualized as made up by quanta of volume which in turn are separated by quanta of area (at the intersections and on the links, respectively). Hence, we can visualize a spin network as sitting on the dual of a cellular de-composition of physical space.¹⁰ As far as the dynamics of spin networks is concerned, there is still another, more recent approach, which appears to be promising as to the further development of topological aspects of quantum gravity (referred to as TQFT). In setting out to develop this new ansatz¹¹, John Baez notes that although originally, Penrose thought of spin networks in terms of describing the geometry of space-time, they really turn out to describe the geometry of space much better. His idea is therefore, to supplement loop quantum gravity with an appropriate path-integral formalism. While in traditional quantum field theory, path integrals are calculated using Feynman diagrams, he would like to introduce two-dimensional analogues of the latter, called spin foams. ¹²Basically, a spin foam is a two-dimensional complex built from vertices, edges, and polygonal faces, with the faces labelled by group representations, and the edges labelled by intertwining operators. If we take a generic slice of a spin foam, we get a spin network. Hence, a spin foam is essentially taking one spin network into another, of the form F: Y®Y. Just as spin networks are designed to merge the concepts of quantum state and geometry of space, spin foams shall serve the merging of concepts of quantum history and geometry of space-time.¹³ Very much like Feynman diagrams do, also spin foams provide for evaluating information about the history of a transition of which the amplitude is being determined. Hence, if Y and Y are spin networks with underlying graphs g and g, then any spin foam F: Y®Y determines an operator from L2(Ag /Gg) to L2(Ag /Gg) denoted by O such that <F, O F> = <F, Y><Y, F> for any states F, F. The evolution operator Z(M) is a linear combination of these operators weighted by the amplitudes Z(O). Obviously, we can define a category with spin networks as objects and spin foams as morphisms. This leads to a discrete version of a path integral. Hence, re-arrangement of spin numbers on the combinatorial level is equivalent to an evolution of states in terms of Hilbert spaces in the quantum picture and effectively changes the topology of space on the cobordism level. This can be understood as a kind of manifold morphogenesis in time: Visualize the n-dimensional manifold M (with ¶M = S È S - disjointly) as M: S ® S, that is as a process (or as time) passing from S to S. This the mentioned cobordism. Note that composition of cobordisms holds and is associative, but not commutative. The identity cobordism can be interpreted as describing a passage of time when topology stays constant. Visualized this way, TQFT might suggest that general relativity and quantum theory are not so different after all. In fact, the concepts of space and state turn out to be two aspects of a unified whole, likewise space-time and process. So what we have in the end, is a rough (and simplified) outline of the foundations of emergence, in the sense that we can localize the fine structure of emergence (the re-arrangements of spin numbers in purely combinatorial terms being visualized as a fundamental fluctuation) and its results on the macroscopic scale (as a change of topology being visualized by physical observers). This is actually what we would expect of a proper theory of emergence. These results can also be formulated in the language of category theory: As TQFT maps each manifold S representing space to a Hilbert space Z(S) and each cobordism M: S ® S representing space-time to an operator Z(M): Z(S) ® Z(S) such that composition and identities are preserved, this means that TQFT is a functor Z: nCob ® Hilb. Note that the non-commutativity of operators in quantum theory corresponds to non-commutativity of composing cobordisms, and adjoint operation in quantum theory turning an operator A: H ® H into A*: H ® H corresponds to the operation of reversing the roles of past and future in a cobordism M: S ® S obtaining M*: S ® S. So what we do realize after all is that spin networks, in particular as being visualized in terms of their quantum deformations, turn out in these models as the fundamental fabric of the world, in the sense that they are underlying and eventually actually producing the world of classical physics. On the other hand, these networks can be thought of as representing the most fundamental channels of information transport: It is in fact quantum computation which is permanently being performed through the channels the spin networks provide. The latter serve as a kind of universal lattice through which the information produced by quantum computation is percolating such that an eventual clustering in the sense of percolation theory spontaneously creates the onset of classicity. The actual route taken is that via the formation of knots in terms of Wilson loops. That is, in the end, the classical world can be visualized equivalently as a condensation of knotted spin networks. More recently, a similar path (but with different conclusions) has been taken by Stuart Kauffman and Lee Smolin: They basically utilize a deterministic model of directed percolation to achieve similar results and show that this can be visualized as a cellular automaton.¹⁴

The idea is then to give the necessary criteria for a percolation phase transition which renders the system behaviour critical, as a derivation from Kauffmans idea of a fourth law of thermodynamics: He basically asks whether we can find a sense in which a non-ergodic Universe expands its total dimensionality, or total work space in a sustainable way as fast as it can. He then refers to Smolins interpretation of spin networks and their knotted structures at Planck scale level as comprising space itself.¹⁵

He suggests that knotted structures are combinatorial objects rather like molecules and symbol strings in grammar models, and he expects that such systems become collectively autocatalytic - practically showing up as knots acting on knots to create knots in rich coupled cycles not unlike a metabolism: The connecting concept will be that those pathways into the adjacent possible along which the adjacent possible grows fastest will simultaneously be the most complex and most readily lead to quantum decoherence, and classicity. If complexity breeds classicity, then the Universe may follow a path that maximizes complexity.¹⁶

This is in fact his concept of a fourth law: that the adjacent possible will be attained which could account for the explicit semantics and dynamics of evolution.

For illuminating discussions while in Cambridge I would like to thank John Baez, Julian Barbour, Richard Bell, Mary Hesse, Chris Isham, David Robson, Lee Smolin, John Spudich, and Steve Vickers. In particular, I thank Paola Zizzi for important discussions and advice, and for inviting me to her institute at Padova. I also thank Basil Hiley for his interest in this topic and the discussions we had, as well as for giving me the occasion to present this conception to his physics theory group at Birkbeck College London.