Der Satz von Pythagoras ein Satz über Quadrate?

Satz. In einem rechtwinkligen Dreieck ist die Summe der Quadrate über den Katheten gleich dem Quadrat über der Hypotenuse.
Satz. In einem rechtwinkligen Dreieck ist die Summe der Flächeninhalte der Halbkreise über den Katheten gleich dem Flächeninhalt des Halbkreises über der Hypotenuse.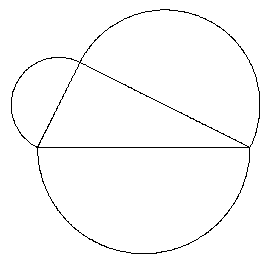
Satz. In einem rechtwinkligen Dreieck ist die Summe der Flächeninhalte der regelmäßigen Sechsecke über den Katheten gleich dem Flächeninhalt des regelmäßigen Sechsecks über der Hypotenuse.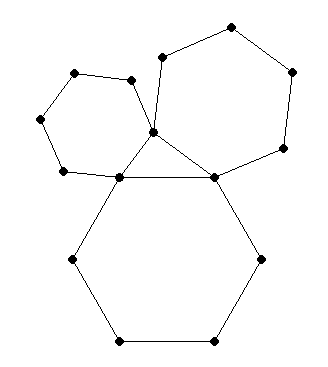
u.s.w.

Alle diese Aussagen sind richtig, denn wir betrachten jeweils Flächen, die proportional zum Quadrat der Grundseite sind! (Ein Halbkreis mit Grundseite x hat den Flächeninhalt π/8.x², ein regelmäßiges Sechseck mit Kantenlänge x hat den Flächeninhalt (3√3).x²,...)

Die charakteristische Eigenschaft, die wir hier verwenden, ist die Ähnlichkeit der jeweiligen Figuren, die über den drei Seiten errichtet werden:

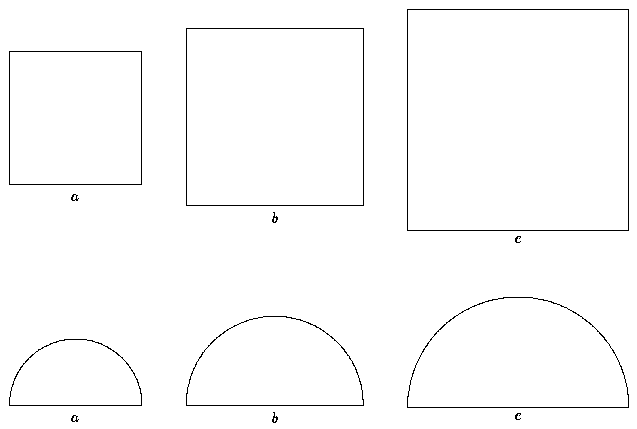
Satz. Ein rechtwinkliges Dreieck habe Katheten a,b und Hypotenuse c. Seien F(a), F(b), F(c) ähnliche Figuren (dabei sei b/a der Proportionalitätsfaktor, der F(a) in F(b) überführt, und c/b derjenige, der F(b) in F(c) überführt). Dann ist der Flächeninhalt von F(c) die Summe der Flächeninhalte von F(a) und F(b).

Alle diese Aussagen für beliebige Flächen sind zueinander äquivalent - es genügt, einer dieser Aussagen zu beweisen. Üblicherweise wird die Quadrat-Aussage genommen - Es geht aber einfacher!

Naber's Beweis: Gegeben sei das Dreieck mit Katheten a,b und Hypotenuse c.

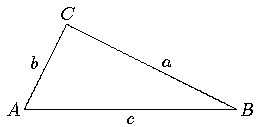
Fälle das Lot vom Eckpunkt C (gegenüber von c) auf die Hypothenuse c, der Lotfußpunkt sei D.

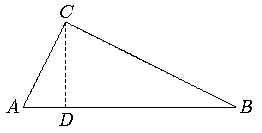
Behauptung: Die Dreiecke ABC, ACD und CBD sind ähnlich (und haben die Grundseiten c, a und b). (Beweis: trivial).

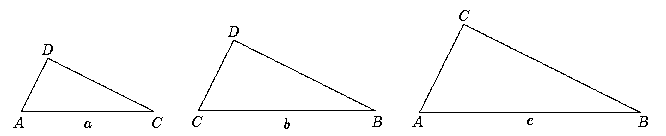
Also betrachten wir die zueinander ähnlichen Flächen

Damit ist alles bewiesen!

Also kann man den Satz des Pythagoras auch folgendermaßen formulieren:

Satz. In einem rechtwinkligen Dreieck ist die Summe der Kringel über den Katheten gleich dem Kringel über der Hypotenuse.