
 |
 |
 |




| 
|
| |
| |

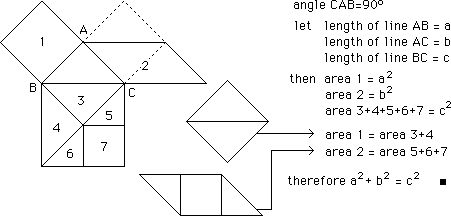
Developing Geometry Understandings and Spatial Skills through Puzzlelike Problems
with Tangrams: Tangram Puzzles
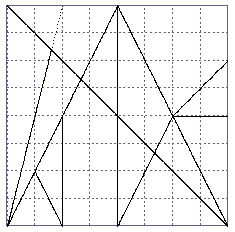
Bis auf die rechte obere Ecke handelt es sich um Steine fast wie beim normalen Tangram -
aber trotzdem ist Vorsicht geboten: So ist das Parallelogramm hier eine Raute!
Frage: Lässt sich aus diesen Steinen ein Qudrat legen?
Umformulierung: Gilt:
Nein!
Quadratische Körpererweiterungen:
Tangram im Schul-Unterricht
Die Studie Principles and Standards for School Mathematics
von NCTM ("National Council of Teachers of
Mathematics")
hat einen eigenen Abschnitt mit folgendem Titel:

Unterstützt werden diese Zielsetzungen von vielen Institutionen,
allerdings ist sie wegen ihrer Abkehr vom traditionellen Mathematik-Unterricht
auch umstritten.
Mathematische Aufgabenstellungen
Objectives:

Man braucht die Flächeninhalte der Tangram-Steine: Es gibt
Demnach gibt es vier Möglichkeiten zum Aufteilen:
1.Möglichkeit 4+4 1+1+Q+P+D
2. 4+1+1+D 4+Q+P
3. 4+1+1+Q 4+D+P
4. 4+1+1+P 4+D+Q
zum Beispiel:
Fixiert man die Lage des Parallelogramms, so ist die Lage aller anderen Steine
fixiert.
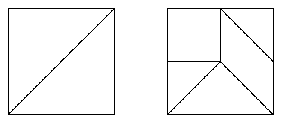

Zum Beispiel:
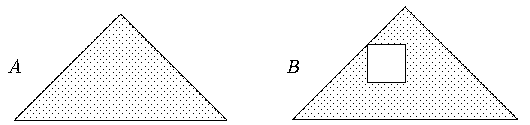
Die Lösungen:
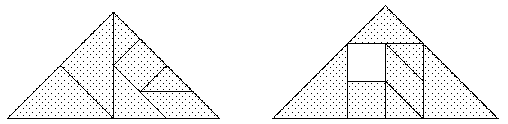
Analoge Puzzles
Von Nob, einem berühmten japanischen Puzzle-Erfinder, stammt eine
Tangram-Variante, die mit einem festen quadratischen Rahmen arbeitet;
es gibt gelbe und rote Steine, die den Tangram-Steinen nachempfunden sind,
und die zusammen den Rahmen vollständig ausf¨llen. Das Spiel wird
unter dem Titel "Shape by Shape" von der Firma Binary Arts
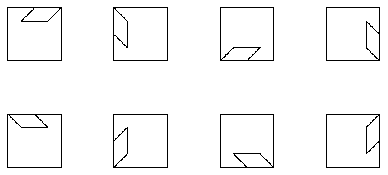
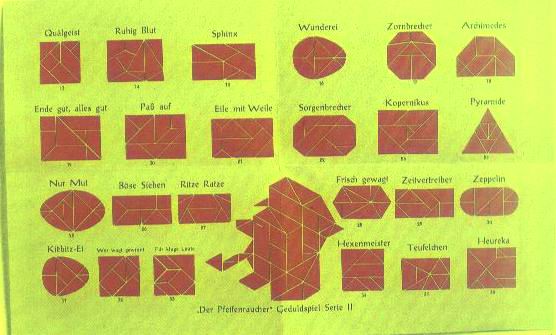
vertrieben. Folgende Formen werden je zweimal verwandt:
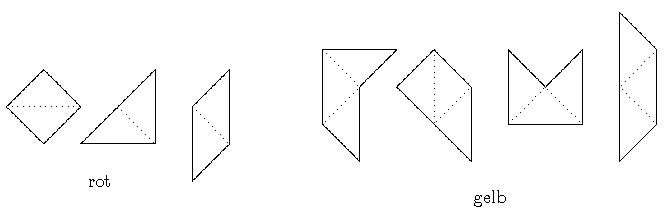
Bei den drei roten Formen handelt es sich um alle möglichen Kombinationen
von zwei kongruenten gleichschenkligen rechtwinkligen Dreiecken; entsprechend
handelt es sich bei den vier gelben Formen um alle möglichen Kombinationen
von drei derartigen Dreiecken. Basis-Figur ist hier also (wie beim
echten Tangram) ein gleichschenkliges rechtwinkliges Dreieck. Die sechs roten
Teile bestehen aus insgesamt 12 Basisdreiecken, die 8 gelben aus insgesamt
24 Basisdreiecken, insgesamt gibt es also 36 Basisdreiecke, die in folgenden
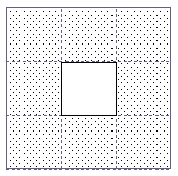
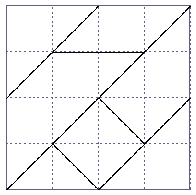
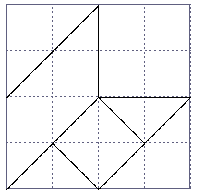
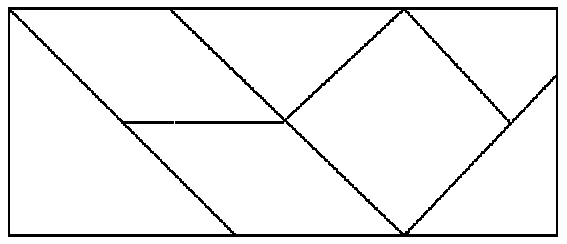
Rahmen einzupassen sind (jedes Quadrat entspricht zwei Basisdreiecken):

Folgerungen:


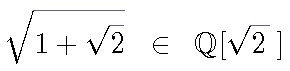
Wurzeln
Ziemlich alle Fragen, die mit dem Tangram zu tun haben,
spielen sich in folgendem Körper ab:
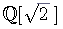

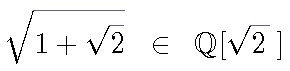 nicht richtig ist?
nicht richtig ist?
 |
 |
 |