Flexagone

Ein Hexaflexagon

(Vorlage als pdf-File, als ps-File)

Die beiden punktierten Flächen sind aufeinander zu kleben, und zwar wie folgt:

Hier noch einmal die Vorderseite, zusammen mit einer Faltlinie: der rechte Teil wird nach hinten geklappt.
Wir erhalten folgendes Bild:

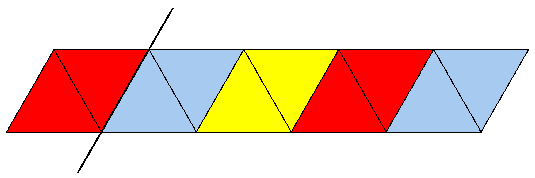
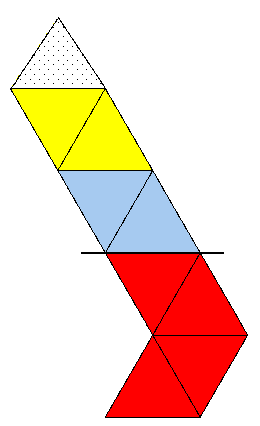
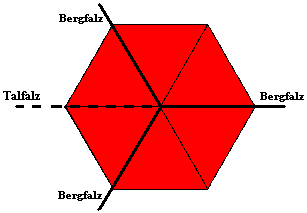
Eingezeichnet ist schon die nächste Faltlinie: nun wird der obere Teil nach hinten geklappt.
Als letztes wird der linke Teil nach hinten geklappt:
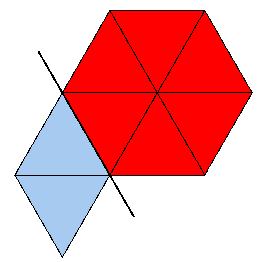
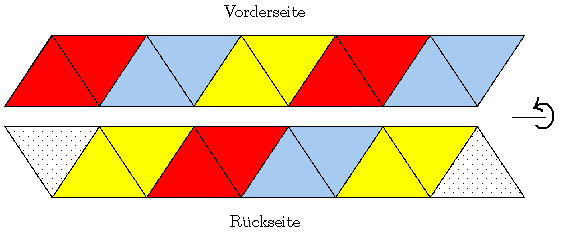
Danach liegen die beiden schraffierten Flächen aufeinander und müssen verklebt werden.

Was ist das besondere an Flexagonen?
Falten man das Sechseck wie folgt:

so erhält man eine Raute, die man wieder zu einem Seckseck enthaften kann:

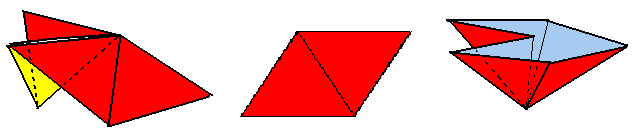
Durch deratiges Zusammenfalten und Neuentfalten erhät man ganz verschiedene Ansichten:

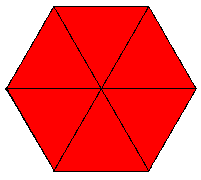
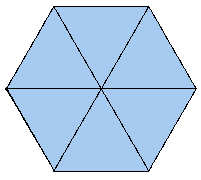
Insgesamt gibt es (nach dem Zusammenkleben) 18 Dreiecke, und zwar 6 rote, 6 blaue und 6 gelbe - durch das Falten und Entfalten sieht man also nacheinander alle Dreiecke, unabhängig davon, ob sie zur Vorder- oder zur Rückseite des Papierstreifens gehörten.

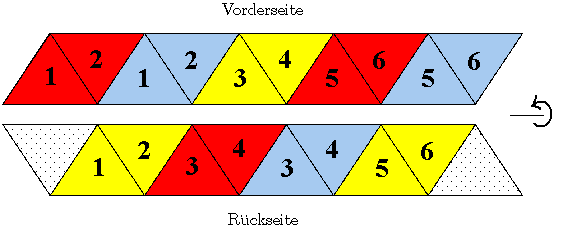
Die Klappsequenz, die wir bei der Konstruktion des Flexagons verwandt haben, entspricht gerade der Bildung eines Möbiusbands, und zwar dem Band B₃, das durch dreifaches Verdrehen entsteht:

Um genauer verfolgen zu können, was beim Zusammenfalten und Neuentfalten passiert, nummerieren wir die Dreiecke:

Das Flexagon ist aus folgenden Dreier-Kombinationen zusammengesetzt, die sich partiel überdecken:

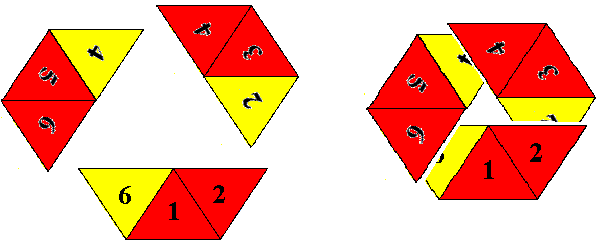
Schauen wir uns nun das Zusammenfalten und Neuentfalten an:

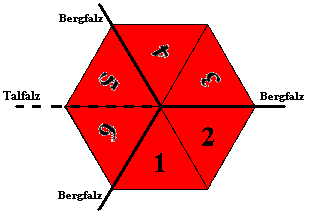
Nach dem Entfalten erhalten wir folgende Konfiguration:

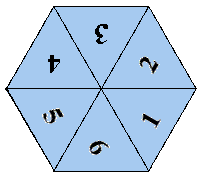
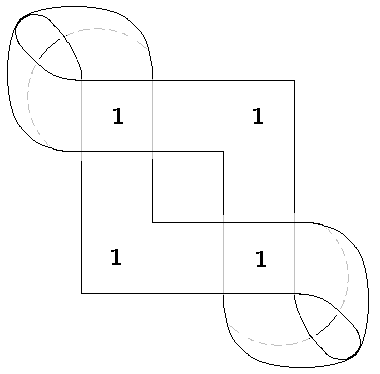
Wir sind im Möbiusband gerade eine Stelle nach rechts gewandert!

Zur Geschichte:

Es wird berichtet, dass die ersten Flexagone von Arthur Stone 1939 entwickelt wurden: Er war damals Graduate Student in Princeton.

Ein Flexagon aus 8 Quadraten

Hier ein weiteres einfaches Flexagon, das zwei Papierstreifen mit jeweils 5 Quadraten verwendet:

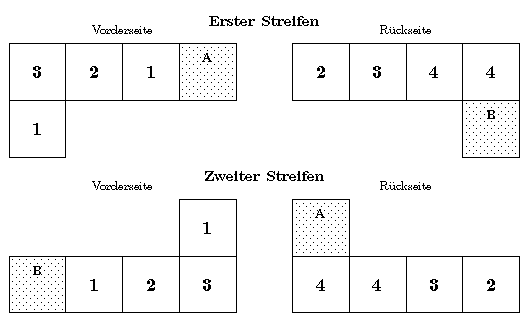
(Vorlage als pdf-File, als ps-File)

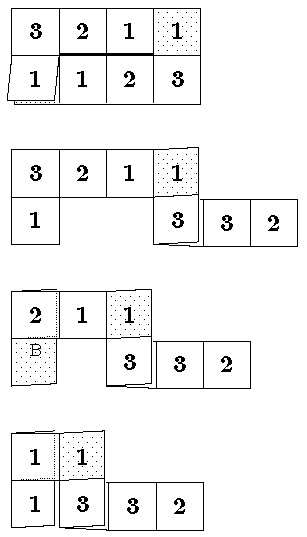
Es sind die beiden Streifen auszuschneiden (die einzelnen Felder sollten beschriftet oder bemalt werden, zum Beispiel eben mit den Zahlen 1 bis 4).

Die punktierten Felder werden geeignet verklebt, A auf A und B auf B.

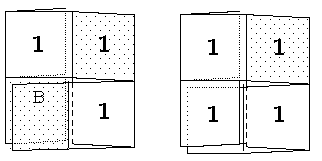
Würden wir einfach die beiden Streifen aufeianderlegen, und A auf A, B auf B kleben (genauer: das A auf der Unterseite des zweiten Streifens auf das A des ersten Streifens, und das B auf der Unterseite des ersten Streifens auf das B des zweiten Streifens kleben)
so erhielten wir eine 4×2-Fläche mit einem Schlitz - nichts Aufregendes: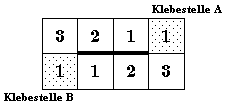

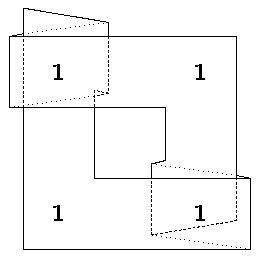
Vor dem Zusammenkleben werden die einzelnen Streifen gefaltet, und zwar:

Handelt es sich wieder um ein Möbius-Band?

Wie man sieht, handelt es sich hier um das Band B₂, also um kein Möbiusband!

Weitere Informationen über Flexagone. Insbesondere findet man hier weitere Vorlagen wie zum Beispiel das Tetrahexaflexagon