WWW   

    FAKULTÄT FÜR MATHEMATIK
Interaktive Kommunikation, Diagnose und Vorhersage in Netzwerken


Darstellung der erreichten Ergebnisse


Erstantrag


I Interaktive Kommunikation


A Interaktive Datenübertragung


1. Informationsflüsse

Unser Vortrag am 23.07.2002 in Konstanz konzentrierte sich auf den Min-Max Satz aus [5] über Informationsflüsse in Netzwerken. Neben dem üblichen Kopieren von Daten ist auch Codieren von weiterem Vorteil und führt zu einem optimalen Ergebnis. Damit ist der Unterschied von Informationsflüssen und Güterflüssen in Netzwerken vollständig verstanden. Während die Multi-user Informationstheorie für die wir den ersten Kanalcodierungssatz bereitstellten ([A12], [A18], []), mit Schwierigkeiten stochastischer Störungen und Korrelationen kämpfte und nur kleine Zahlen von Sendern und Empfängern behandeln konnte, zeigt der neue Satz, dass auch schon für störungsfreie Kanäle echte Probleme entstehen und gelöst werden konnten - und zwar für ganze Netzwerke von Kommunikatoren. Inspiriert durch den Vortrag haben Peter Sanders und seine Koautoren S. Egner und L. Tolhuizen [] den Existenzsatz um einen effizienten Algorithmus bereichert (Vortrag ``Polynomial time algorithms for networks information flow'' am 27.03.2003 in Tübingen). Dieses Ergebnis und die Arbeiten unseres langjährigen Mitarbeiters Ning Cai und Koautoren ([P1], [P2]), die den Min-Max Satz in Standardrichtungen (z.B. für störende aber unabhängige Kanäle) weiterführen, wurden auf dem von den zwei vom DFG geförderten Miniworkshops mit den Teilnehmern diskutiert. Neuere weiterführende Forschungsvorhaben werden in Sektion 3 formuliert. Es wurden 15 Vorträge gehalten, die in Anlage 4 zu finden sind.


2. Konnektoren


Der Beitrag der Kieler Baltz, Jäger und Srivastav [9] über Konnektoren die Bielefelder Gruppe besonders angeregt (Vortrag von Anand Srivastav ``Algorithms and Design for Multicast Networks'' am 27.03.2003 in Tübingen) und zu den Arbeiten [P15] und [P3] geführt.

Das Problem des Entwurfs von optimalen Konnektoren (``rearrangeable networks'') geht auf die Pionierarbeiten von Shannon [21], Slepian [22], Clos [12] und Benes [10] zurück.

Gegeben $ n,N\in\mathbb{N}$ $ (n\leq N)$ , sei $ G=(V,E)$ ein Digraph, dessen Knotenmenge $ V=I\cup L\cup O$ partitioniert ist in Eingangsknoten $ I$ , Verbindungsknoten $ L$ und Ausgangsknoten $ O$ , so dass $ \vert I\vert=n$ , $ \vert O\vert=N$ und für jede injektive Abbildung $ f:I\to O$ es einen Knoten-disjunkten Pfad gibt, der $ i$ mit $ f(i)$ verbindet, für alle $ i\in I$ . Dann heisst $ G$ ein $ (n,N)$ -Konnektor.

Ein $ (n,N)$ -Konnektor heisst $ (n,N,d)$ -Konnektor, falls jeder Ausgang von jeden Eingang aus via eines Pfades der Länge $ \leq d$ erreicht werden kann. $ e(n,N,d)$ ist die minimale Kantenanzahl solcher Konnektoren. Symmetrische Konnektoren, d.h. $ (n,n,d)$ -Konnektoren sind untersucht worden in [19], [20], [14]. Oruc [17] hat als erster $ (n,N,d)$ Konnektoren konstruiert. Der anspruchsvolle Fall ist $ d=2$ . In [9] wird bewiesen, dass ein $ (n,N)$ Konnektor der die Bedingungen:
(c1) $ I$ und $ L$ sind vollständig verbunden, (c2) $ \forall x\in O$ ist der Grad $ k$ , $ \deg(x)=k$ und
(c3) $ \forall x,x^{\prime }\in O$ $ (x\neq x^{\prime })$ $ \vert\Gamma(x)\cap\Gamma(x^{\prime })\vert\leq1$ ( $ \Gamma(x)\triangleq$ die Menge der Nachbarknoten von $ x$ ) erfüllt, für $ k\geq \sqrt n$ ein $ (n,N,2)$ -Konnektor ist. Es werden Konstruktionen angegeben, die $ e(n,N,2)\leq \bigl(1+o(1)\bigr)\cdot \left(Nn^{\frac12}+2N^{\frac12}n^{\frac32}\right)$ beweisen. Insbesondere ist $ e(n,N,2)\leq\bigl(2+o(1)\bigr)N\sqrt n$ für $ n\leq\sqrt N$ . Wir haben bewiesen ([P3]), dass für $ n\geq 16$ und $ N>N_0(n)$ gilt $ e_{\partial}(n,N,2)\leq\bigl(1+o(1)\bigr)N\log_2n$ . Die Konstruktion basiert auf Schatten und den Eigenschaften im Kruskal-Katona Theorem für den Verband der Teilmengen einer endlichen Menge. Geeignete Parameterwahl ermöglicht die Anwendung des Heiratssatzes. Ferner haben wir bewiesen
Theorem

Ein Graph $ G=(I\cup L\cup O,E)$ mit $ \vert I\vert=n,\vert O\vert=N$ gegeben durch unsere Konstruktion mit Grad $ k$

(i)
ist $ (k-1)$ -Kantenfehler-tolerant;
(ii)
ist $ (k-1)$ -Knotenfehler-tolerant, falls $ \binom{2k-3}{k-1}<n\leq\binom{2k-1}k-k+1$ .
Ferner ist in diesem Fall die Konstruktion asymptotisch optimal.


4. Zufällige Verbreitung in Netzwerken (Random Walks)


Da vom kombinatorischen Standpunkt aus ein Netzwerk ein Graph (Hypergraph) mit gewichteten Kanten ist, ist die Untersuchung von Eigenschaften von Graphen von Interesse. In der aktuellen Arbeit [A194] haben wir gezeigt, wie unser Resultat über die Zahl von gekennzeichneten Hypergraphen angewendet werden kann, um das Volumen des gigantischen $ k$ -Kerns in einem zufälligen Hypergraphen zu bestimmen. $ k$ -Kern bedeutet hier, dass jeder Knoten des Hypergraphen inzident mit mindestens $ k$ Kanten ist.

``Process-Level Large Deviations'' für stückweise homogene Random Walks spielen eine Schlüsselrolle bei der Untersuchung von probabilistischen Eigenschaften der Verbreitung von Daten in Netzwerken. Das normale Schema von zwei Flüssen wird beschrieben durch einen Random Walk in zwei Halbräumen mit unterschiedlichen Dynamiken in jedem Raum. Das Problem der grossen Abweichungen wurde für diesen Fall in [11] gelöst. Gleichzeitig ist dieses Problem im Falle von mehr als zwei homogenen Teilen weitaus schwieriger und nur wenig ist darüber bekannt.


5. Kommunikationskomplexität


In diesem Gebiet sind keine Arbeiten entstanden. In den 80-er Jahren haben wir intensiv auf diesem Gebiet gearbeitet. Erinnert sei an die Arbeiten ([A61], [A81], [A82], [A88], [A93], [A120]). Ferner sei auf inzwischen umfangreiche Lehrbuchliteratur verwiesen.


B Interaktive Codierungstheorie


Bereits im Erstantrag wurde auf eine Erweiterung der algebraischen Codierungstheorie für mehrere Sender und Empfänger hingewiesen. Die Ergebnisse der bereits erwähnten Arbeit [5] legen es nahe Informationsflüsse in Netzwerken zu untersuchen, die oben genannten Typen von Fehlern unterliegen.


1. Unkonventionelle Fehler und Kodierungen


Es gibt verschiedene unkonventionelle Konzepte von Fehlern wie unidirektionale Fehler, Defekte, Löschungen, Einsetzungen, unsynchronisierte Fehler, lokalisierte Fehler usw., die unkonventionelle Codes zur Erkennung und Korrektur benötigen.

In der Arbeit [P5] haben wir $ q$ -äre Codes eingeführt und untersucht, die in der Lage sind alle unidirektionalen Fehler eines gewissen Levels $ 1\leq\ell\leq q-2$ zu korrigieren. Untere und obere Schranken für die Größe dieser Codes werden präsentiert.

Wir betrachten eine spezielle Art von asymmetrischen Fehlern in einem $ q$ -ären Kanal. Das Alphabet $ \mathcal{Q}$ besteht aus den ganzen Zahlen $ \{ 0,1,\dots,q-1\}$ und für jeden gesendeten Vektor $ x=(x_1,\dots,x_n)$ ist der Ausgang von der Form $ (x_1+e_1,\dots,x_n+e_n)$ , wobei ``$ +$ '' für die Addition von reellen Zahlen steht und $ x_i+e_i\leq q-1$ , $ i=1,\dots,n$ . Wir sagen, dass ein asymmetrischer Fehler $ e=(e_1,\dots,e_n)$ vom Level $ 1\leq l\leq q-1$ ist, falls $ 0\leq e_i\leq l$ . Wir sagen auch, dass $ t$ asymmetrische Fehler aufgetreten sind, falls für das Hamming-Gewicht $ wt_H(e)=t$ gilt. Entsprechend sagen wir, dass $ t$ unidirektional Fehler aufgetreten sind, falls der Ausgang entweder $ x+e$ oder $ x-e$ ist. Wir betrachten $ q$ -äre Codes, die alle asymmetrischen oder unidirektionalen Fehler eines gegebenen Levels $ l$ korrigieren. Dementsprechend benutzen wir die Abkürzungen $ l$ -AAEC- und $ l$ -AUEC-Codes. Für gegebenes $ 1\leq l\leq q-2$ sei $ A_a(n,l)_q$ und $ A_u(n,l)_q$ die maximale Zahl von Codewörtern in einem $ q$ -ären Code der Länge $ n$ , der alle asymmetrischen bzw. unidirektionalen Fehler korrigiert. Es ist klar, dass $ A_u(n,l)_q\leq A_a(n,l)_q$ . Es stellt sich heraus, dass man leicht $ A_a(n,l)_q$ für alle Parameter $ 1\leq l\leq q-2$ und $ n$ bestimmen kann. Dies trifft jedoch für den Fall von unidirektionalen Fehlern nicht zu.

Theorem 1 (i) Für $ 1\leq l\leq q-2$ gilt $ A_a(n,l)_q=\left\lceil\frac{q}{l+1}\right\rceil^n$ und folglich auch $ A_u(n,l)_q\leq \left\lceil\frac{q}{l+1}\right\rceil^n.$
(ii) $ A_u(n,l)q\geq c\frac{\left\lceil\frac{q}{l+1}\right\rceil^n}{\sqrt{n}}$
(iii) $ A_u(n,1)_3\geq c\frac{2^n}{n^\frac{1}{2\log_2 3}}$ , für eine Konstante $ c$ .

Zunächst betrachten wir Codes, die über eine gewisse lineare Gleichung über den reellen Zahlen definiert sind. Gegeben $ \mathcal{Q}=\{ 0,1,\dots,q-1\}\subset \mathbb{R}$ und $ a_0,\dots,a_{n-1},a\in \mathbb{Z}$ sei

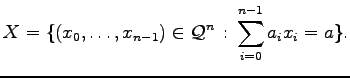
$\displaystyle X=\{(x_0,\dots,x_{n-1})\in\mathcal{Q}^n\, :\, \sum_{i=0}^{n-1}a_ix_i=a\}.$

Für gegebene $ l,q,n$ definiere $ LA_u(n,l)_q$ als die maximale Größe eines $ l$ -AUEC-Codes über dem Alphabet $ q$ , der durch obige lineare Gleichung definiert wird. Entsprechend benutzen wir $ LA_a(n,l)_q$ für $ l$ -AAEC-Codes.

Theorem 2 $ LA_a(n,l)_q=LA_u(n,l)_q.$

Theorem 3 (i) Für $ l\geq 1$ und $ q>2(l+1)$ , gilt $ c \left(\frac{q}{l+1}\right)^n \leq LA_u(n,l)_q\leq\left\lceil\frac{q}{l+1}\right\rceil^{n-1}$ für eine Konstante $ c$ .
(ii) Für $ l+1\vert q$ gilt $ LA_u(n,l)_q=\left(\frac{q}{l+1}\right)^{n-1}.$

Das Problem des Schutzes gegen unidirektionale Störungen entsteht in Systemen mit optischer Nachrichtenübertragung, beim Entwurf von fehlertoleranten sequentiellen Maschinen, in asynchronen Systemen usw.


2. Synchronisation und Delay


In [P19] werden Synchronisationscodes mit konstanter Blocklänge $ n$ besprochen. Es wird eine Konstruktion eines Codes mit Abstand $ t=2^k$ und Blocklänge $ n=t\cdot r$ angegeben. Diese Konstruktion ist optimal für genügend großes $ n$ und fest gewähltes $ t$ .

Ein binäres deBruijn Netzwerk der Ordnung $ n$ ist ein ungerichteter Graph $ \cal B^n = ({\cal V}^n,{\cal E}^n)$ , wobei $ {\cal V}^n=\mathcal{X}^n$ die Knotenmenge ist und $ (u^n,v^n)\in {\cal E}^n$ ist eine Kante genau dann wenn

$\displaystyle u^n\in \{ (b,v_1,\dots ,v_{n-1}),(v_2,\dots ,v_n,b) : b\in \{0,1\} \}.$




Eine Teilmenge $ \mathcal{A}\subset {\cal V}^n$ heißt unabhängig, falls keine zwei Knoten aus $ \mathcal{A}$ verbunden sind. Wir bezeichnen mit $ {\mathcal I}({\mathcal B}^n)$ die Menge aller unabhängigen Teilmengen eines DeBruijn-Netzwerkes. Es gilt, dass fúr alle $ b\in \{0,1\}$ , $ (b,b,\dots b)\not\in \mathcal{A} \in {\mathcal I}({\mathcal B}^n)$ , denn $ (b,b,\dots b)$ ist von sich selbst abhängig. Die Unabhängigkeitszahl $ f_{\mathcal{B}}(n)$ von $ \mathcal{B}^n$ ist $ f_{\mathcal{B}}(n)=\max\limits_{\mathcal{A}\in {\mathcal I}({\mathcal B}^n)} \mid \mathcal{A}\mid$ .


C Interaktive Identifikation


1. Allgemeine Theorie des Informationstransfers, gemeinsame Zufälligkeit (Common Randomness), Zufallszahlen


Alle hier dargestellten Ergebnisse wurden in Kooperation mit dem DFG-Projekt AH46/1-1,1-2, 4-1 erzielt. Ausserdem soll die Forschung in einem neubeantragten DFG-Projekt fortgeführt werden.

Nehmen wir an, eines von $ N$ möglichen Ereignissen hat sich zugetragen. Die Shannon'sche Informationstheorie beschäftigt sich mit der Frage ``Welches Ereignis hat sich zugetragen?''. Bei der Identifikation fragt man ``Hat sich Ereignis $ i$ zugetragen?''. Dabei ist $ i$ irgendein Element aus $ {1,2,\dots,N}$ . Erlaubt man eine kleine Fehlerwahrscheinlichkeit, so kann man (auch für störende Kanäle) durch randomisierte Strategien die Identifikation mit $ O(\log\log N)$ Bits durchführen, während das herkömmliche, naive Verfahren $ \log N$ Bits benötigt. Dieses Phänomen wurde in [A58] entdeckt und analysiert. Genauer wurde gezeigt, daß in erster Näherung mit $ n$ Bits gerade eines von $ N=\exp\{\exp\{Cn\}\}$ vielen Objekten identifiziert werden kann. Hierbei ist $ C$ die bekannte Shannonsche Kanalkapazität, d.h. in erster Näherung kann gerade eine von $ N=\exp\{Cn\}$ vielen Nachrichten übertragen werden. Es ist überraschend, daß bei beiden Problemen dieselbe Konstante auftritt, d.h. die Identifikationskapazität 2-ter Ordnung ist gleich Shannon's Übertragungskapazität 1-ter Ordnung.

Die Theorie ist inzwischen in verschiedene Richtungen weit entwickelt worden. Sie ist von mehreren Autoren (Anantharam, Bassalygo, Bäumer, Burnashev, Cai, Csiszár, Han, Kleinewächter, Narayan, van der Meulen, Verboven, Verdu, Yang, Zhang). Fundamentale Phänomene sind:
im Gegensatz zum Übertragungsproblem erhöht Rückkopplung die Kapazität eines diskreten gedächtnislosen Kanals, Störung kann die Identifikationskapazität vergrößern, als entscheidender Parameter erweist sich die ``gemeinsame Zufälligkeit''.
Diese neue Codierungstheorie gibt neue Einblicke in die alte: bemerkenswerte Dualitäten stellen sich ein, Probleme die in einer Theorie schwierig sind, sind oft einfach in der anderen und umgekehrt. Neue Forschungsgebiete entstanden: Approximation von Ausgangsverteilungen eines Kanals durch geeignete Approximation von Eingangsverteilungen, neue Kryptographische Modelle, und neue Fragen an die Erzeugung von Zufallszahlen.
In [P23] haben wir Ideen, Probleme und Resultate mitgeteilt, mit denen wir uns in der vergangenen Dekade beschäftigt haben. Sie erweitern die Grenzen der Informationstheorie in mehreren Richtungen. Die wichtigsten Beiträge betreffen Informationstransfer für Kanäle. Es gibt auch neue Fragen und einige Antworten in neuen Modellen der Datenkompression. Während viele Untersuchungen noch in einer Anfangsphase sind, haben andere das Stadium ausgereifter mathematischer Theorien erreicht.
Insbesondere wird eine allgemeine Theorie des Informationstransfers vorgestellt, die auf natürliche Weise für störende Kanäle Shannon's Theorie der Informationsübertragung und die von uns initiierte Theorie der Identifikation (ausgearbeitet mit G. Dueck) als Extremfall umfasst. Wir beweisen mehrere neuartige Codierungssätze für zufällige Eincodierungen. Auf der Seite der Quellencodierung führen wir das neue Konzept der Identifikationsentropie ein.
Schließlich kommen wir über die Informationstheorie hinaus zu neuen Lösungskonzepten für stochastische Algorithmen.
(Zum Beispiel: für ein $ i$ hat ein Polynom eine Nullstelle im i-ten Intervall oder nicht?). Die Algorithmen sollen schnell sein und keine Fehlerwahrscheinlichkeiten haben. Jedes algorithmische Problem kann so analysiert werden. Dieses geht weit über die Informationstheorie hinaus.

Die Theorie der Identifikation fand interessante Anwendungen bei Alarmsystemen ([]) und Wasserzeichen ([], [], []). Wie in [] herausgestellt wurde ist die Kombination von Übertragungscodes und Identifikationscodes nützlich für gewisse Aufgaben der Identifikation über einen ``multiple-access'' Kanal. Dies kann z.B. für öffentliche Notdienste zutreffen, die in einem Gebiet viele Arten von verschiedenen Anfragen einer großen Zahl von Individuen versorgen, die für sich genommen selten eine kurze Nachricht gefolgt von einer Anfrage senden. Unter Wasserzeichensignierung versteht man eine Methode, geheime Information in eine Nachricht (z.B. ein Bild) einzubetten, die weder entfernt noch dekodiert werden kann ohne Zugriff auf den geheimen Schlüssel. Dieses kann zum Schutz von Urheberrechten eingesetzt werden. Eine sehr ausführliche Liste mit Referenzen hierzu findet man in [A186].


2. Watermarking


Wir haben in [P7] die Untersuchungen von Y. Steinberg und N. Merhav fortgesetzt und insbesondere einige ihrer Fragen zur Robustheit bei Watermarking-Identifikations Codes beantwortet.

Beim Watermarking geht es darum, eine geheime Information in einer gegebenen Nachricht zu verbergen, so dass diese von jemandem, dem der geheime Schlüssel unbekannt ist, nicht entfernt und entschlüsselt werden kann. Y. Steinberg und N. Merhav regten an, die folgenden Fälle zu untersuchen.

(i)
Der Angreifer benutzt einen unbekannten Kanal.
(ii)
Der Dekodierer hat partielle Information über die Nachricht.
R. Ahlswede und N. Cai griffen die beiden Anregungen in ihrer Arbeit [P7] auf. Sie untersuchten Watermarking-Identifikations Codes unter der Annahme, dass der Angreifer einen Kanal wählt, der beiden, dem Informationsverberger und dem Dekodierer, unbekannt ist. Für die zweite Anregung untersuchten sie zwei Modelle. In ihrem ersten nahmen sie an, dass gemäß der Ursprungsnachricht der Informationsverberger komponentenweise einen Schlüssel erzeugt und zum Dekodierer schickt, der als Nebeninformation im standardmäßigen Sinn der Informationstheorie betrachtet wird. Im zweiten Modell kann der Informationsverberger den Schlüssel in beliebiger Weise wählen und die einzige Restriktion ist, dass die Schlüssel-Rate beschränkt ist. Untere Schranken in all den oben beschriebenen Fällen wurden in [A186] erzielt und von diesen wird vermutet, dass sie scharf sind.

Da die Internet-Technologie sich so schnell entwickelt, ist der Schutz des Urheberrechts offensichtlich von immer größerer Bedeutung. Wir bemerken hier, dass nach unserer Kenntnis der Angriffs-Kanal in [A186] zu den robustesten der in dieser Richtung untersuchten zählt.

In der Arbeit [P8] werden Anwendungen von Watermarking ausführlich dargestellt.


3. Identifizierbare Eltern Eigenschaft (IPP, identifiable parent property)


Um gegen Software Piraterie geschützt zu sein, haben H.D.L. Hollmann, J.H. van Lint, J-P. Linnartz, und L.M.G.M. Tolhuizen in [13] Codes mit identifizierbarer Eltern Eigenschaft (IPP) wie folgt eingeführt. Es sei $ \mathcal{X}$ ein endliches Alphabet. Wir sagen eine Folge $ x^n\in\mathcal{X}^n$ ist ein Nachkomme der Folgen $ a^n, b^n\in\mathcal{X}^n$ oder $ a^n$ und $ b^n$ sind Eltern von $ x^n$ , falls für $ t=1,\dots,n$ $ x_t\in\{a_t,b_t\}$ . Eine Teilmenge $ \mathcal{C}\subset \mathcal{X}^n$ heisst IPP-Code, falls für jeden Nachkommen eines Paars von Folgen aus $ \mathcal{C}$ zumindest eine Eltern-Folge identifiziert werden kann (ohne Fehler). Die obigen Autoren waren an der maximalen Größe von IPP-Codes interessiert. Mit elegeanten Ideen konnten sie Schranken für einige der Parameter herleiten. Jedoch ist im allgemeinen das Problem weit offen, sogar was die asymptotischen Raten betrifft.

R. Ahlswede und N. Cai [P9] bemerkten, dass das Problem in [13] als das folgende Kommunikationsproblem für Multiple-Access Kanäle (MAC) umformuliert werden kann. Sei $ W$ ein MAC für den $ \mathcal{X}$ beide Eingangsalphabete und das Ausgangsalphabet darstellt und $ W(z\vert x,y)=\frac{1}{2}$ genau dann, wenn $ z=x \textrm{ oder }y$ ist, für alle $ x,y,z\in\mathcal{X}$ . Dann hat ein Code $ \mathcal{C}\subset \mathcal{X}^n$ die IPP Eigenschaft genau dann, wenn der Dekodierer des MAC wenigstens eins der Codewörter $ a^n$ und $ b^n$ mit Wahrscheinlichkeit $ 1$ bestimmen kann, falls die Sender unabhängig voneinander und beliebig Codewörter $ a^n$ und $ b^n$ aus $ \mathcal{X}^n$ auswählen und sie über den Kanal schicken. R. Ahlswede und N. Cai haben wie folgt ein alternatives Modell ``mit zwei Geschlechtern'' betrachtet. Gegeben ein MAC dessen Eingangsalphabete $ \mathcal{X}$ und $ \mathcal{Y}$ und Ausgangsalphabet $ \mathcal{Z}$ nicht notwendigerweise gleich sind. Sie suchten ein Paar von Codes $ \mathcal{U}\subset \mathcal{X}^n$ und $ \mathcal{V}\subset \mathcal{Y}^n$ mit maximaler Summe der einzelnen Raten $ \frac{1}{n}\log \vert\mathcal{U}\vert+\frac{1}{n}\log \vert\mathcal{V}\vert$ , so dass der Empfänger wenigstens eines der Codewörter $ u^n\in \mathcal{U}$ und $ v^n\in\mathcal{V}$ mit beliebig kleiner durchschnittlicher Fehlerwahrscheinlichkeit oder mit Null-Fehlerwahrscheinlichkeit dekodieren kann, falls die zwei Sender $ u^n$ und $ v^n$ über den Kanal schicken. In der Variante mit zwei Geschlechtern bestimmten R. Ahlswede und N. Cai die optimale Summe der Raten oder die Kapazität für beliebig kleine durchschnittliche Fehlerwahrscheinlichkeit in [P9]. Die zwei Gründe für den Erfolg sind:

(i)
Wie üblich ist es in Informations- und Kodierungstheorie einfacher, die Kapazität als die Null-Fehler-Kapazität zu bestimmen.
(ii)
Für zwei Geschlechter ist es einfacher, ein Elternteil zu identifizieren als es für ein einzelnes Geschlecht ist.


D Broadcasting


In [P10] betrachten wir ein Kommunikationssystem mit einem Sender (oder Kodierer) $ E$ und zwei Empfängern (oder Dekodierern) $ D_1$ und $ D_2$ mit störungsfreiem Feedback und ungleichem Fehlerschutz. Der Sender $ E$ möchte simultan eine Nachricht $ i \in {\cal M}_1$ an $ D_1$ (Dekodierer 1) und eine Nachricht $ j \in {\cal M}_2$ an $ D_2$ (Dekodierer 2) schicken und er kodiert jedes Paar $ (i,j)$ von Nachrichten in eine binäre Folge der Länge $ n$ .

Diese Folge wird an die zwei Empfänger über zwei unabhängige Kanäle geschickt. Wegen der Störung des Kanals kann die Ausgabefolge, die von den zwei Empfängern erhalten wurde, in höchstens $ t_1=n\tau_1$ bzw. $ t_2=n\tau_2$ Bits Fehler enthalten. Desweiteren nehmen wir an, dass es störungsfreien Feedback gibt. Das heisst, der Sender darf das $ m$ -te Bit der Eingabe abhängig von den ersten $ (m-1)$ Bits beider Ausgabefolgen wählen. Wir nennen den Code einen binären $ (n, M_1, M_2, (t_1, t_2))$ Feedback Code (oder kurz einen FB-Code) für den Broadcast Kanal wenn $ \vert{\cal M}_k\vert = M_k$ für $ k=1,2$ . Ein Codewort ist von der Form $ c\left(i,j,y_1^{n-1},y_2^{n-1}\right)=\left(c_1\left(i,j\right), \dots,c_k\lef... ...y_1^{k-1},y_2^{k-1}\right),\dots,c_n\left(i,j,y_1^{n-1},y_2^{n-1}\right)\right)$ , wobei $ c_k:{\cal M}_1 \times {\cal M}_2 \times {\cal Y}_1^{k-1} \times {\cal Y}_2^{k-1} \to {\cal X}$ eine Funktion für den $ k$ -ten Code-Buchstaben ist, welche abhängt von der Nachricht die wir übermitteln möchten und den $ (k-1)$ Bits die von Dekodierer 1 und 2 erhalten wurden, wobei $ {\cal X}={\cal Y}=\{0,1\}$ . Zudem nennen wir $ c$ eine gemeinsame Strategie (des Senders und der Empfänger).

Wir präsentieren einen Code der eine bessere Rate als der in [8] gibt, wobei Feedback nur einmal während der gesamten Übertragung benutzt wird. Die Idee ist es, die $ n$ Bits in zwei Runden zu schicken. Zuerst übermittelt der Sender $ \lceil \log M_2\rceil$ Bits (die binäre Darstellung der Nachricht für $ D_2$ ). In der zweiten Runde kodiert er das Fehlermuster der ersten Runde und die Nachricht für $ D_1$ . Die Idee erst die Bits für $ D_2$ zu schicken ist ähnlich zur Idee die in [2] benutzt wird. Wir präsentieren zudem eine äußere Schranke für die Ratenregion. Wir leiten diese äußere Schranke her indem wir die Idee des Isoperimetrischen Satzes für Hammingräume benutzen. Wir leiten eine untere Schranke für die Anzahl der möglichen Ausgabefolgen für jede Familie von Kodierfunktionen und jede Menge von Fehlermustern eines $ (n, M_1, M_2, (0, t))$ Feedback Codes her.

Weitere Probleme aum Broadcasting sollen im neubeantragten Projekt ``Informationsflüsse'' untersucht werden.


II Diagnose


Die in diesem Abschnitt beschriebenen Suchprobleme sollen in einem neubeantragten Projekt weiter untersucht werden.

1. Diagnose als Suchen mit beschränkten Mengen


Bei der Analyse der Arbeit [15] zur Überdeckung von Knoten für die Fehlerdiagnose im Hyperkubus

haben wir bemerkt, dass die Essenz ein Suchproblem darstellt mit Restriktionen an die Teilmengen $ A_1,\dots,A_N$ , die als Fragen gestellt werden, ob sie das unbekannte Element $ x\in\{1,2,\dots,M\}$ enthalten.

Schon Renyi fragte nach dem minimalen trennenden System $ (A_1,\dots,A_N)$ mit $ \vert A_i\vert\leq k$ für $ i=1,\dots,N$ .

Katona gab eine Entropieschranke als untere Schranke für $ N$ an und eine etwas andere obere Schranke, die von Wegener verbessert wurde (siehe Ahlswede/Wegener Suchprobleme).

Überraschenderweise - diese Resultate nun schon seit mehreren Dekaden kennend - interessierte uns nun, ob diese Entropieschranke scharf ist, wenigstens approximativ und wir waren in der Lage dies zu beweisen ([P28]). Während eine standardmäsige zufällige Wahl der Menge selbst bei nicht beschränkten Mengen bekanntlich ([]) um einen Faktor 2 vom Optimum entfernt ist, gelingt jetzt die Lösung mit nur einigen Experten bekannten Expurgationstechnik der Informationstheorie.

Ferner, wenn die Teilmengen durch Hammingkugeln in $ \{0,1\}^n$ ersetzt werden, gelangen wir immer noch zur Entropieschranke. Dieses löst das obige Problem zur Fehlerdiagnose.


2. Delay


Als nächstes fassen wir die Ergebnisse der Arbeit [P11] zusammen.
Es ist wohlbekannt, dass Suchprobleme mit einer stochastischen Antwortmatrix, die sich unabhängig für die Fragen verhält, äquivalent formulieren lassen als Übertragungsprobleme für eine diskreten gedächtnislosen Kanal (DMC) mit Rückkopplung.

Das wird in Kapitel 3 des Buches [] von R. Ahlswede und I. Wegener beschrieben.

Dort werden auch Ahlswedes Kodierungsschema für den DMC und auch für beliebig variierende Kanäle (AVC) beschrieben, die die Kapazitäten erreichen. Das letztere kann als robustes Modell der Suche angesehen werden.

In [P11] haben wir für $ d$ -Verzögerungs binäre Such Codes eine Ungleichung vom Kraft-Typ gefunden, die mit obiger äquivalent ist.


3. Sequentielle Suchmodelle mit Fehlern


4. Monotonicity Testing and Property Testing


III Vorhersagetheorie in Netzwerken


Lars Bäumer, dessen Dissertation Vorhersagetheorie in Verbindung mit Identifikation behandelte, hat nicht wie bei der Antragsstellung geplant an diesem Projekt mitgearbeitet, da er mein Forschungsprojekt am Zif als Assistent unterstützt.

Er hat sich dort biologischen Fragestellungen zur Evolution von Sprachen und zur Tierkommunikation gewidmet. Vorhersagetheorie wurde deshalb in diesem Projekt nicht betrieben. Die BAT IIa-Stelle dieses Projektes hatte durchgehend Harout Aydinian inne.


IV Zwischenspeicher Managementstrategien in Netzwerken und Creating Order

Christian Wischmann wird dieses Thema in seiner Doktorarbeit behandeln. Seine ersten Ergebnisse präsentierte er auf dem Jahreskolloquium in Aachen 2006.

1.Fortsetzungsantrag


I Interaktive Kommunikation


A Interaktive Datenübertragung


1. Informationsflüsse

Unsere Arbeit [A155] aus dem Jahre 2000 hat mittlerweile eine neue Forschungsrichtung begründet. Dies wird deutlich, wenn man sich die ``Network Coding Home Page'' von Ralf Koetter (``http://tesla.csl.uiuc.edu/$ \sim$ koetter/NWC/index.html''), unser Buch [6] oder auch die Kapitel 11 und 15 des Lehrbuches [23] anschaut.

Nach der Datenbank von R. Koetter wurden weltweit nur eine handvoll Arbeiten in der Netzcodierung vor dem Jahr 2001, aber dann 8 Arbeiten 2002, 23 Arbeiten 2003 und über 25 Arbeiten in der ersten Hälfte von 2004 veröffentlicht, usw.

Die Forschung zur Netzcodierung wächst schnell. Microsoft, IBM und andere Firmen haben Abteilungen eingerichtet, die dieses neue Gebiet erforschen. Einige amerikanische Universitäten (Princeton, MIT, Caltech und Berkeley) haben auch Forschungsgruppen in der Netzcodierung aufgebaut. Der heilige Gral in der Netzcodierung soll (auf eine automatisierte Art und Weise) Netzflüsse (wobei Netzcodierung verwendet wird) in einer durchführbaren Weise planen und organisieren.

Die meisten gegenwärtige Forschungen behandeln dieses schwierige Problem noch nicht.

Wir berichten hier über die Arbeit [P14], in der weitere grundlegende Erkenntnisse gewonnen wurden. Wir zeigen, daß die Aufgabe des Entwerfens von leistungsfähigen Strategien für Informationsnetzflüsse (Netzcodierungen) eng mit dem Konstruieren von fehlerkorrigierenden Codes zusammenhängt. Siehe dazu insbesondere unten die Proposition 3 in der eine Bijektion zwischen Netzwerkflüssen und einer Klasse fehlerkorrigierender Codes gezeigt wird. Diese Verbindung überrascht, da sie für Netze auftritt, in denen keine Fehler vorkommen!

Erinnert sei an die traditionelle Verwendung dieser Codes zum Rückschluss auf Nachrichten, die durch unbekannte Fehler gestört sind.

Um in den Reichtum dieser Ideen einzuführen, zeigen wir, dass die Lösung für Flussprobleme für bestimmte einfache Netze mathematisch gleichwertig ist mit der Beantwortung der Frage nach der Existenz orthogonaler lateinischer Quadrate, bei der sich bekanntlich Euler gründlich irrte. Eine vollständige Lösung wurde erst in der zweiten Hälfte des 20ten Jahrhunderts gefunden (``The Euler spoilers'' Bose/Parker/Shrikhande).

Gegeben sei das folgende Netz:


\epsfig{figure=figure1.eps, width=0.5 \textwidth}


Wir nehmen an, dass die Nachrichten $ x,y$
aus einem endlichen Alphabet
$ A=\{1,2,\dots,n\}$ sind.

wollen $ x$ und $ y$ reproduzieren.







Proposition 1 Es gibt eine Bijektion zwischen den Lösungen dieses Flussproblems und den Paaren der orthogonalen lateinischen Quadrate der Ordnung $ \vert A\vert$ .

Proposition 2 (Korollar zur Lösung von Eulers Problem):

Das Flussproblem in der Abbildung hat eine Lösung genau dann, wenn das zugrundeliegende Alphabet nicht 2 oder 6 Elemente hat.

Netzcodierung und seine Verbindungen zu fehlerkorrigierenden Codes
Die Aufgabe der Konstruktion von orthogonalen lateinischen Quadraten kann als Spezialfall der Konstruktion von fehlerkorrigierenden Codes gesehen werden. Es gibt, z.B., eine Bijektion zwischen den orthogonalen lateinischen Quadraten der Ordnung $ \vert A\vert$ und den $ (4, \vert A^2\vert, 3)$ $ \vert A\vert$ -ären fehlerkorrigierenden Codes.

Betrachten wir sodann das folgende Flussproblem:


\epsfig{figure=figure2.eps, width=0.8 \textwidth}

Jeder Kanal in diesem Netz hat die Kapazität eine Nachricht (pro Zeiteinheit) zu übertragen. Nehmen wir an, die Aufgabe sei, zwei Nachrichten $ x,y\in A$ von dem oberen Punkt zu jedem der 10 unteren Punkte zu schicken. Es kann gezeigt werden, dass dieses Flussproblem eine Lösung über dem Alphabet $ A$ hat genau dann, wenn ein $ (5, \vert A\vert^2, 4)$ $ \vert A\vert$ -ärer fehlerkorrigierender Code existiert. Es ist bekannt, dass solche Codes existieren, genau wenn $ \vert A\vert\notin\{2,3,6\}$ .

Das Flussproblem kann verallgemeinert werden. Betrachten wir ein Netz $ N_{k,r,s}$ , das aus $ k$ Nachrichten $ x_1,x_2,\dots,x_k\in A$ besteht, die von einem Quellpunkt aus übertragen werden. Der Quellpunkt wird mit einer Menge verbunden, die $ r$ Punkte enthält, und für jede $ s$ -elementige Teilmenge (es gibt $ \binom rs=\frac{r!}{(r-s)!s!}$ viele), haben wir einen Terminalpunkt. Die Aufgabe ist es, jede Nachricht $ x_1,x_2,\dots,x_k\in A$ in jedem der Terminalpunkte zu reproduzieren. Das vorhergehende Netzflussproblem entspricht $ N_{2,5,2}$ .

Allgemeiner kann gezeigt werden:

Proposition 3 Das Flussproblem $ N_{k,r,s}$ hat genau dann eine Lösung, wenn ein $ (r, \vert A\vert^k, r-s+1)$ $ \vert A\vert$ -ärer fehlerkorrigierender Code existiert.

Diese Codes sind gerade die $ \vert A\vert$ -ären Maximalabstand Codes von Singleton 1964.

Ferner kann man zeigen, dass das Informationsfluss Problem $ N_{8,16,11}$ keine lineare Lösung über $ {\mathbb{F}}_2$ hat, während eine nicht lineare Lösung existiert.

Sind solche Phänomene nur sporadisch oder weitverbreitet?

Für ein anderes Netz mit horizontalen und vertikalen Flüssen kann gezeigt werden, dass optimale vertikale Flüsse einem optimalen Minimalabstand Code entsprechen. Diese wurden in [1] Anticodes genannt und vollständig charakterisiert.

Dieses Beispiel ist ein Schlüsselbeispiel, das zeigt, dass die klassische Theorie der fehlerkorrigierenden Codes weiter entwickelt werden muss, um als Grundlage für die Netzcodierung zu dienen. Schlechteste Codes traten schon früher in der Kryptographie auf ([3],[4]).

Dieses von uns begründete Forschungsgebiet soll in einem neu beantragten DFG-Projekt ``Informationsflüsse'' weiter erforscht werden.


2. Konnektoren


Ein $ (N,n)$ -Konnektor der Tiefe $ d$ ist ein azyklischer Digraph mit $ n$ Eingängen und $ N$ Ausgängen, in dem für jede injektive Abbildung der Eingangsknoten in die Ausgangsknoten, $ n$ knotendisjunkte Wege der Länge höchstens $ d$ existieren, die jeden Eingang mit seinem entsprechenden Ausgang verbinden. In Fortsetzung der Arbeit [P3] haben wir wiederum das Problem betrachtet, zwei Konnektoren mit $ n\ll N$ und geringer Tiefe zu konstruieren.

In Verfolgung unseres Zieles, den Schattensatz von Kruskal/Katona für die Posets, die Familien der Teilmengen einer endlichen Menge sind, durch Schattensätze in anderen Posets zu ersetzen, kamen wir auf den Satz von Leeb für Posets des Produktes von Sternen und waren damit erfolgreich. Eine einfache Konstruktion liefern Konnektoren der Größe $ O(N\log n/\log\log n)$ ([P15]).

Die vorher besten Resultate über die Größe von Konstruktionen von $ (n,N,2)$ -Konnektoren waren

- $ O(N\sqrt{n})$ für $ n\leq \sqrt{N}$ von Hwang/Richards 1985,

- $ 2N\sqrt{n}$ für beliebiges $ N\geq n^2$ von Baltz/Jäger/Srivastav 2003,

- $ (1+o(1))N\log_2n$ für alle $ N$ von Ahlswede/Aydinian 2003 ([P3]).

Ein einfaches probabilistisches Argument (Baltz/Jäger/Srivastav, 2003) zeigt die Existenz derartiger Konnektoren der Größe $ O(N)$ , wenn $ n\leq N^{1/2-\varepsilon}, \varepsilon >0$ . Eine genauere Rechnung liefert $ (1+o(1))N$ für alle $ N$ und $ n=$O$ \bigl(N^{1/\sqrt{\log_2N}}\bigr)$ ([P15]).


3. Interaktive Datenübertragung zum Zwecke des Rechnens


Es wird folgendes Modell zugrunde gelegt. $ n$ Prozessoren $ P_1,\dots , P_n$ führen Rechnungen durch und kommunizieren dabei über ein vorgegebenes Netzwerk. Prozessor $ P_i$ kennt das $ i$ -te Argument von $ f$ und möchte den Funktionswert berechnen $ (1\leq i\leq n)$ . In jedem diskreten Zeitpunkt kann er ein Bit an andere Prozessoren übertragen. Diese Bits stehen in Beziehung zu seiner Rechnung oder können auch zufällig erzeugt werden.

Die Rechnung heißt privat, wenn kein Prozessor irgendwelche Informationen über die Argumente der anderen bekommen hat. Ziel ist es die Übertragungsdauer für die Berechnung zu minimieren.

In der Diplomarbeit ([P16]) von Frau Laumann wurde unter Anderem ein Algorithmus von Chor und Kushilevitz für die $ t$ -private Berechnung der $ XOR_n$ -Funktion angegeben. Obere und untere Schranke stimmen überein falls $ n$ ungerade ist. Eine kleine Lücke bleibt falls $ n$ gerade ist. Frau Laumann gelang es durch Verfeinerung des Algorithmus diese Lücke zu schließen.


4. Zufällige Verbreitung in Netzwerken (Random Walks)


Das im Fortsetzungsantrag 2003 vorgeschlagene Problem wurde gelöst. In [P17] wird die asymptotische Formel für die Anzahl der skalierten Schrittfunktionen mit Einschränkung der Länge und Höhe der Schritte des gegebenen Bereichs in der Nachbarschaft einer gegebenen Kurve (Formen der Young Diagramme) angegeben. Dies erlaubt uns, die Asymptotik der Anzahl solcher Funktionen zu finden.


5. Kommunikationskomplexität


B Interaktive Codierungstheorie


1. Unkonventionelle Fehler und Kodierungen


Das Problem des Schutzes gegen unidirektionale Störungen entsteht in Systemen mit optischer Nachrichtenübertragung, beim Entwurf von fehlertoleranten sequentiellen Maschinen, in asynchronen Systemen usw.

Wir setzten diese Arbeit in [P18] fort und betrachteten wieder Codes über dem Alphabet $ Q=\{0,1,\ldots, q-1\}$ zur Kontrolle von unidirektionalen Störungen des Niveaus $ l$ . Das heißt, dass der Übertragungskanal so gestaltet ist, dass das empfangene Wort nicht gleichzeitig eine größere und eine kleinere Komponente als das übertragene Wort enthalten kann. Außerdem ist der Absolutwert der Differenz zwischen einer übertragenen Komponente und seiner empfangenen Version höchstens $ l$ .

Wir studieren die $ q$ -ären Codes, die alle unidirektionalen Störungen des Niveaus $ l$ beheben ($ l$ -UEC Codes). Wir geben neue Konstruktionen und Schranken für solche Codes an. $ A_u(n,l)_q$ sei die maximale Größe eines solchen $ q$ -ären $ l$ -UEC Codes für $ 1\leq l\leq q-1$ . Unsere Hauptresultate sind die folgenden.

Theorem 1. Für jedes $ q$ und $ \ell$ existiert eine positive Konstante $ K$ , so dass für jedes $ n$ gilt

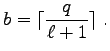
$\displaystyle A_u(n,\ell)_q \geq K b^n n^{-\frac{1}{2}\log_q b},$    wobei $\displaystyle b = \lceil\frac{q}{\ell + 1}\rceil \; . $

Darüberhinaus studieren wir die Klasse der $ l$ -UEC Codes, genannt VT-Typ Codes (Varshamov-Tennengolts Typcodes), die mittels einer linearen Gleichung über den reellen Zahlen definiert werden. Sei $ LA_u(n,l)_q$ die maximale Größe solcher Codes, wenn die Parameter $ n$ , $ q$ und $ l$ gegeben sind. Wir geben eine Konstruktion für optimale Codes (Codes, die die obere Schranke erreichen) für eine große Klasse der Parameter $ q$ , $ l$ und für beliebige Längen $ n$ an. Die konstruierten Codes haben den Vorteil eines sehr einfachen Decodierungsalgorithmus.

Theorem 2. Sei $ q=(b-1)(\ell+1)+d$ für $ 1\leq b-1<d\leq\ell$ . Dann gilt für jedes $ n$

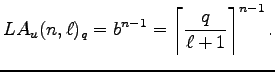
$\displaystyle LA_u(n,\ell)_q=b^{n-1}= \left\lceil\frac q{\ell+1}\right\rceil^{n-1}.$

Die unkonventionellen Fehler sollen auch in dem neubeantragten Projekt fortgesetzt werden.


2. Synchronisation und Delay


In [P20] verallgemeinern wir die Resultate von Ahlswede, Balkenhol, Partner (siehe Fortsetzungsantrag 2003). Wir geben eine Konstruktion f''ur $ T$ -Verschiebungs-Synchronisationscodes an. Es werden untere und obere Schranken f''ur die maximale Gr''oße solcher Codes bewiesen. Man erh''alt so eine unendliche Familie von konstruierten Codes, die sich als optimal erweisen. Alle S''atze gelten auch f''ur beliebige $ q$ -''are Alphabete.

In ([P21]) erzielten wir einen wesentlichen Fortschritt im Beweis der $ 3/4$ -Vermutung von Ahlswede, Balkenhol, Khachatrian [A118] für fixfree Codes im $ q$ -ären Fall. Der Beweis basiert auf einer Verallgemeinerung der deBruijn-Netzwerke. Wir erhalten folgendes

Theorem 1.

Sei $ (\alpha_l)_{l\in {\mathcal N}}$ eine Folge nicht-negativer ganzer Zahlen mit $ \sum_{l=1}^{\infty}\alpha_l q^{-l}\leq {3\over 4}$ . Setze $ L_{\min}=\min\{l:\alpha_l>0\}$ und $ L_{\max}=\sup\{l:\alpha_l>0\}$ . Falls $ L_{\max}<\infty$ , $ L_{\min}\geq 2$ und $ \alpha_l\leq q^{L_{\min} -2} \left\lfloor {q\over 2}\right\rfloor^2 \left\lceil {q\over 2}\right\rceil^{l-L_{\max}}$ , dann existiert ein fixfree Code mit $ \alpha_l$ Codewörtern der Länge $ l$ .

Theorem 2. $ (\alpha_l)_{l\in\mathcal N}$ erfülle $ \alpha_1=\alpha_2=\cdots =\alpha_{n-1}=0$ und $ \sum\limits_{l=1}^{\infty}\alpha_lq^{-l}\leq\frac 34.$

(i) Angenommen $ \frac{\alpha_n}{q^n}+\frac{\alpha_{n+1}}{q^{n+1}} \geq \lceil\frac q2\rceil\frac 1q,\ \alpha_n=L\cdot\lceil\frac q2\rceil$ für ein $ L\in\{1,\cdots ,q^{n-1}\}$ und es existiert ein $ \lceil\frac q2\rceil$ -regulärer Untergraph in dem deBruijn-Netzwerk $ {\cal B}_q(n-1)$ mit $ L$ Knoten, dann gibt es auch einen fixfree Code zur Folge $ (\alpha_l)_{l\in\mathcal N}.$

(ii) Wenn $ \frac{\alpha_n}{q^n}\geq \lceil\frac q2\rceil\frac 1q$ ist, dann existiert ein fixfree Code zur Folge $ (\alpha_l)_{l\in\mathcal N}$ .


C Interaktive Identifikation


1. Allgemeine Theorie des Informationstransfers, gemeinsame Zufälligkeit (Common Randomness), Zufallszahlen


Alle hier dargestellten Ergebnisse wurden in Kooperation mit dem DFG-Projekt AH46/1-1,1-2, 4-1 erzielt. Ausserdem soll die Forschung in einem neubeantragten DFG-Projekt fortgeführt werden.

Störungsfreie Identifikation für Quellen

Wir kommen nun zu einem der Höhepunkte unserer Ergebnisse, nämlich der Entdeckung einer neuen Entropie, die wir Identifikationsentropie nennen.

In [P24] haben wir fehlerfreie Quellencodierung für Identifikation eingeführt, verschiedene Gütemaße definiert und erste Ergebnisse hergeleitet.

Vor der Beschreibung unseres Modells erinnern wir zunächst an den 1. Fundamentalsatz der Informationstheorie.

Shannon hat 1948 gezeigt, dass eine Quelle $ ({\mathcal U},P,U)$ mit Prob $ (U=u)=P_u$ mit einem Präfixcode $ \mathcal C=\{c_u:u\in{\mathcal U}\}\subset\{0,1\}^*$ codiert werden kann, so dass für Boltzmanns Entropie gilt

$\displaystyle H(P)=\sum_{u\in{\mathcal U}}-p_u\log p_u\leq\sum_{u\in{\mathcal U}} p_u\vert\vert c_u\vert\vert \leq H(P)+1,$ (1)

wobei $ \vert\vert c_u\vert\vert$ die Länge des Codewortes $ c_u$ ist.

Für die Quelle und den Präfixcode definieren wir nun eine Zufallsvariable $ C$ mit $ C=c_u=(c_{u1},c_{u2},\dots,c_{u\vert\vert u\vert\vert})$ , falls $ U=u$ .

Wir benutzen den Präfixcode für die störungsfreie Identifikation, das heißt, dass ein Benutzer, der etwa wissen möchte, ob der Quellausgang $ u$ ist, also ob $ c_u=C$ ist, oder nicht, dieses feststellen kann. Er überprüft wiederholt, ob $ C=(C_1,C_2,\dots)$ mit $ c_u$ im ersten, zweiten usw. Buchstaben übereinstimmt und stoppt, wenn der erste verschiedene Buchstabe auftritt, oder wenn $ C=c_u$ ist. Wie groß ist die erwartete Anzahl $ L_{\mathcal C}(P,u)$ der Überprüfungen?

Hiermit in Verbindung stehende Größen sind

$\displaystyle L_{\mathcal C}=\max_{1\leq u\leq N}L_{\mathcal C}(P, u),$ (2)

die erwartete Anzahl von Tests für eine Person im ungünstigsten Fall, falls der Code $ \mathcal C$ verwendet wird.

Weiterhin ist

$\displaystyle L(P)=\min_{\mathcal C}L_{\mathcal C}(P),$ (3)

die erwartete Anzahl Tests im ungünstigsten Fall für den besten Code. Schließlich, falls Benutzerinteresse per Zufallsvariable $ V$ unabhängig von $ U$ gewählt wird und Prob$ (V=v)=Q_v$ für $ v\in\mathcal V=\mathcal U$ definiert wird (siehe [P6], Abschnitt 5), betrachten wir

$\displaystyle L_{\mathcal C}(P, Q)=\sum_{v\in\mathcal U}Q_vL_{\mathcal C}(P,v),$ (4)

die durchschnittliche Anzahl der erwarteten Tests, wenn der Code $ \mathcal C$ verwendet wird, und auch

$\displaystyle L(P, Q)=\min_{\mathcal C}L_{\mathcal C}(P,Q),$ (5)

die durchschnittliche Anzahl der erwarteten Tests für einen besten Code. Ein natürlicher Spezialfall ist die mittlere Anzahl der erwarteten Tests

$\displaystyle \bar L_{\mathcal C}(P)=\sum_{u=1}^N\frac1NL_{\mathcal C}(P, u).$ (6)

Dies entspricht $ L_{\mathcal C}(P,Q)$ , falls $ Q=\left(\frac1N, \dots, \frac1N\right)$ und

$\displaystyle \bar L(P)=\min_{\mathcal C}\bar L_{\mathcal C}(P).$ (7)

Ein anderer mathematisch interessanter Spezialfall ist der Fall $ Q=P$ . Hier schreiben wir

$\displaystyle L(P, P)=\min_{\mathcal C}L_{\mathcal C}(P,P).$ (8)

So wie Shannon sich für die Abschätzung der Größe $ \min_{\mathcal C} \sum_{u\in \mathcal U} p_u\vert\vert c_u\vert\vert$ interessierte, so interessiert uns jetzt die Abschätzung der soeben definierten Größen. Instruktiv sind dabei Huffman Codes, die unter dem Shannon Kriterium, der mittleren Codewortlänge, alle strikt optimal sind. Bei der Identifikation erhält man ein differenzierteres Bild.

Beispiel: $ N=\vert\mathcal U\vert=10$ , $ P$ Gleichverteilung. Es gibt $ \binom{2^3}{10-2^3}=28$ Huffman Codes.
Die 4 schlechtesten Huffman Codes sind maximal unausgeglichen, wie zum Beispiel

unit=0.7cm
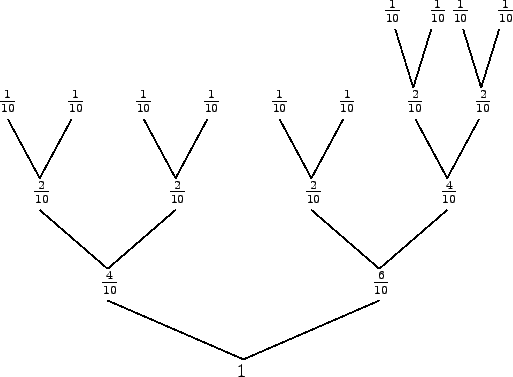
\begin{pspicture}(11,9) \put(11,8){$1\over 10$} \put(10,8){$1\over 10$} \put(9.5... ...\psline(3,1.3)} \put(5.4,0.4){\psline(-3,1.3)} \put(5.25,0){$1$} \end{pspicture}

In diesem Fall gilt $ L_{\mathcal C}(P)=2.2$ und $ L_(P,P)=1.880$ , da

$\displaystyle L_{\mathcal C}(P)$ $\displaystyle =1+0.6+0.4+0.2=2.2$    
$\displaystyle L_{\mathcal C}(P, P)$ $\displaystyle =\frac1{10}[1.6\cdot4+1.8\cdot2+2.2\cdot4]=1.880.$    


Einer der 16 besten Huffman Codes sieht folgendermaßen aus:

unit=0.7cm
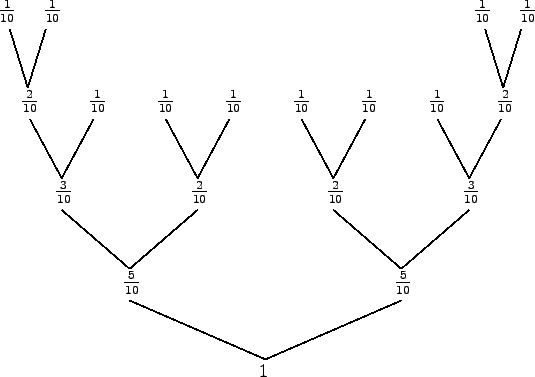
\begin{pspicture}(11,9) \put(11,8){$1\over 10$} \put(10,8){$1\over 10$} \put(-0.... ...\psline(3,1.3)} \put(5.4,0.4){\psline(-3,1.3)} \put(5.25,0){$1$} \end{pspicture}

In diesem Fall gilt: $ L_{\mathcal C}(P)=2.0$ und $ L_{\mathcal C}(P,P)=1.840$ , weil

$\displaystyle L_{\mathcal C}(P)$ $\displaystyle =L_{\mathcal C}(\tilde c)=1+0.5+0.3+0.2=2.000$    
$\displaystyle L_{\mathcal C}(P, P)$ $\displaystyle =\frac15(1.7\cdot2+1.8\cdot1+2.0\cdot2)=1.840$    

Eine Entdeckung unserer Arbeit ist die Identifikationsentropie, nämlich die Funktion

$\displaystyle H_I(P^N)=2\left(1-\sum_{u=1}^NP^2_u\right) \\ $ (9)

für die Quelle $ (\mathcal U,P)$ , wobei $ \mathcal U=\{1,2,\dots,N\}$ und $ P^N=(P_1,\dots,P_N)$ eine Wahrscheinlichkeitsverteilung ist.

Die Bedeutung von $ H_I(P)$ in der Identifikationsquellencodierung ist sehr ähnlich der klassischen Entropie $ H(P)$ in der fehlerfreien Codierung von Daten: Sie dient als gute Schranke.

Wir haben die folgenden Hauptresultate erzielt:

Theorem 1. Für jede Quelle $ ({\mathcal U}, P^N)$ gilt

$\displaystyle L(P^N)\geq L(P^N, P^N)\geq H_I(P^N).$

Theorem 2. Für $ P^N=(P_1,\dots,P_N)$ gilt

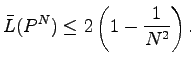
$\displaystyle \bar L(P^N)\leq2\left(1-\frac1{N^2}\right).$

Theorem 3. Für $ P^N=(2^{-\ell_1},\dots,2^{-\ell_N})$ mit 2-er Potenzen als Wahrscheinlichkeiten gilt

$\displaystyle L(P^N, P^N)=H_I(P^N).$

Theorem 4.

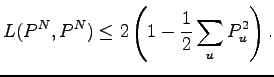
$\displaystyle L(P^N, P^N)\leq 2\left(1-\frac12\sum_uP^2_u\right).$

Für $ P_u=\frac1N(u\in{\mathcal U})$ ergibt dies die obere Schranke $ 2\left(1-\frac1{2N}\right)$ , die besser ist als die Schranke in Theorem 2 für die Gleichverteilungen.

Schließlich erhalten wir

Korollar.

$\displaystyle L(P^N, P^N)\leq H_I(P^N)+\max_{1\leq u\leq N}P_u.$

Es zeigt, dass die unterere Schranke von $ L(P^N,P^N)$ und die obere Schranke nahe zusammen sind. Dies ist eine operationale Rechtfertigung des neuen Entropiebegriffes.

Ferner wurde schon in [P6] gezeigt

Theorem 5.

$\displaystyle L(P^N)\leq 3$

gilt für alle Quellen.

Die Erweiterung auf den allgemeinen $ q$ -ären Fall gibt die Identifikationsentropie

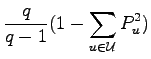
$\displaystyle {q\over q-1} (1-\sum_{u\in \mathcal U} P_u^2)$

und entsprechende Verallgemeinerungen der Theoreme.

In [P25] zeigen wir, dass $ L_\mathcal C(P,Q)^2\leq L_\mathcal C(P,P)L_\mathcal C(Q,Q)$ und dass für einen Blockcode $ \mathcal C$ $ \min_{P\ auf\ \mathcal U} L_\mathcal C(P,P)=L_\mathcal C(R,R)$ gilt, wobei $ R$ die Gleichverteilung auf $ \mathcal U$ ist. Daher gilt $ {\bar L}_\mathcal C(P)\leq L_\mathcal C(P,P)$ für einen Blockcode $ \mathcal C$ . Andererseits gilt für $ P^N= (2^{-ln},\dots, 2^{-ln})$ , $ {\bar L}_\mathcal C(P^N)=2(1-{1\over N})\geq L(P^N,P^N)=H_I(P^N)$ .

Weiterhin erklären wir in [P25] die codierungstheoretische Bedeutung der beiden Faktoren in der Entropieformel.


Korrelationen von pseudo-zufälligen binären Folgen

Im folgenden wird nun über die Arbeit [P27] berichtet. In einer Reihe von Arbeiten untersuchten Mauduit und Sárközy (teilweise mit mehreren Koautoren, unter ihnen die Bielefelder Ahlswede und Khachatrian) endliche pseudo-zufällige binäre (und allgemeiner auch $ q$ -äre) Folgen

$\displaystyle E_N=\{e_1,e_2,\dots,e_N\}\in\{-1,+1\}^N.$

Insbesondere führten sie folgende Pseudo-Zufälligkeitsmaße ein.

Das Wohlverteilungsmaß von $ E_N$

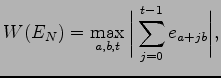
$\displaystyle W(E_N)=\max_{a,b,t}\bigg\vert\sum^{t-1}_{j=0}e_{a+jb}\bigg\vert,$

wobei das Maximum über alle $ a,b,t$ mit $ a,b,t\in\mathbb{N}$ (= die Menge der positiven ganzen Zahlen) und $ a\leq a+(t-1)b\leq N$ genommen wird. Das Korrelationsmaß der Ordnung $ k$ von $ E_N$

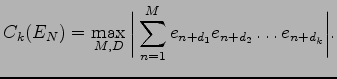
$\displaystyle C_k(E_N)=\max_{M,D}\bigg\vert\sum^M_{n=1}e_{n+d_1}e_{n+d_2}\dots e_{n+d_k}\bigg\vert.$

Hier erstreckt sich das Maximum über alle $ D=(d_1,\dots,d_k)$ und $ M$ , wobei $ d_1<\dots< d_k$ nichtnegative ganze Zahlen sind, für die $ M+d_k\leq N$ gilt.

Die Folge $ E_N$ wird als ``gute'' pseudo-zufällige Folge betrachtet, wenn die Werte $ W(E_N)$ und $ C_k(E_N)$ (zumindest für kleine Werte von $ k$ ) ``klein'' in Abhängigkeit von $ N$ sind (insbesondere sind die beiden Werte $ o(N)$ , wenn $ N\to\infty$ ).

Die verwendete Terminologie ist dadurch berechtigt, dass für ``wirklich zufällige'' $ E_N\in\{-1,+1\}^N$ gilt: Mit Wahrscheinlichkeit ``nahe an 1'' sind die beiden Werte $ W(E_N)$ und (für fixiertes $ \ell$ ) $ C_\ell(E_N)$ ungefähr gleich $ N^{1/2}$ .

In der Arbeit von C. Mauduit und A. Sárközy ``On finite pseudorandom binary sequences I. Measure of pseudorandomness, the Legendre symbol'', Acta Arith. 1997 wird erklärt, warum das Wohlverteilungsmaß und das Korrelationsmaß als Maße für Pseudo-Zufälligkeit verwendet werden können. Es ist jedoch zu erwarten, dass es Anwendungen gibt, bei denen es genügt, nur einige statt aller pseudo-zufälligen Maße zu kontrollieren. Eine der wichtigsten Anwendungen der Pseudo-Zufälligkeit ist die Kryptographie. Wenn wir z.B. eine binäre Folge $ E_N\in\{-1,+1\}^N$ (nach der Umformung in eine Bit-Folge) als Schlüssel-Strom (key stream) im Standard-Vernam-Chiffre verwenden möchten, dann soll $ E_N$ bestimmte Pseudo-Zufälligkeits-Eigenschaften besitzen. Soll $ E_N$ ein kleines Wohlverteilungsmaß und für kleine Werte von $ k$ ein kleines Korrelationsmaß der Ordnung $ k$ haben? Mit anderen Worten, kann der Gegner diese Tatsache ausnutzen und den Code brechen, wenn $ W(E_N)$ , bzw. $ C_k(E_N)$ (für irgendeinen kleinen fixierten Wert von $ k$ ) groß ist? Die natürlichste Vorgehensweise ist die vollständige Suche (exhaustive search): Der Angreifer kann alle binären Folgen $ E_N\in\{-1,+1\}^N$ mit großen Werten von $ W(E_N)$ , bzw. $ C_k(E_N)$ als potentiellen Schlüssel-Strom überprüfen. Offensichtlich ist diese Art des Angriffs tatsächlich nur bedrohend, wenn die Anzahl der Folgen $ E_N\in\{-1,+1\}^N$ mit

(i)
großem $ W(E_N)$ , bzw.
(ii)
großem $ C_k(E_N)$
``viel kleiner'' als die Gesamtzahl $ 2^N$ der Folgen in $ \{-1,+1\}^N$ ist. Außerdem braucht man einen schnellen Algorithmus zur Erzeugung von Folgen der Art (i), bzw. (ii). Fall (i) ist einfach zu behandeln. Fall (ii), d.h. der Fall mit großem Korrelations-Maß, ist viel interessanter. Dieser Fall wird von uns betrachtet.

Für $ k,N\in\mathbb{N},2\leq k\leq N$ und $ 0<\alpha<1$ definiere

$\displaystyle \mathcal F(k,N,\alpha)=\{E_N:E_N\in\{-1,+1\}^N,C_k(E_N)>\alpha N\}.$

Theorem 1. Für jedes $ k\in\mathbb{N}$ mit $ k\geq2$ und jedes $ \varepsilon >0$ gibt es ein $ \delta=\delta(k,\varepsilon )>0$ und ein $ N_o=N_o(k,\varepsilon )$ , so dass für $ N>N_o$ gilt

$\displaystyle \vert\mathcal F(k,N,\varepsilon )\vert<2^{(1-\delta)N}. $

Wir verschärfen das Theorem in dem Spezialfall, wo die Ordnung der Korrelation 2 ist.

Theorem 2. Falls $ 0<\alpha<1$ , $ \varepsilon >0$ , $ N\in\mathbb{N}$ und $ N>N_o(\alpha,\varepsilon )$ , dann gilt

$\displaystyle 2^{(\xi((1-\alpha)/2)-\varepsilon )N}<\vert\mathcal F(2,N,\alpha)\vert< 2^{(\xi((1-\alpha)/2)+\varepsilon )N}. $


2. Watermarking


3. Identifizierbare Eltern Eigenschaft (IPP, identifiable parent property)


D Broadcasting


II Diagnose


Die in diesem Abschnitt beschriebenen Suchprobleme sollen in einem neubeantragten Projekt weiter untersucht werden.

1. Diagnose als Suchen mit beschränkten Mengen


2. Delay


3. Sequentielle Suchmodelle mit Fehlern


Eine der wichtigsten Fragen in Multiprozessor Systemen ist die Verlässlichkeit. Die Fehler Diagnose (Identifikation der fehlerhaften Prozessoren) ist ein Bestandteil bei Erreichung der Fehler-Toleranz.

Preparata/Metze/Chien (1967) führten ein graphentheoretisches Modell für selbstdiagnostizierende Systeme ein. Hierbei geht es um automatische Fehler Diagnose in Multiprozessor Systemen.

Ein System $ S$ ist als ein Graph $ G(V,E)$ modelliert, wobei $ V$ die Menge der Elemente (Prozessoren) und $ E$ die Menge der Verbindungen ist.

Die Prozessoren führen Tests über ihre Nachbarn durch und senden die Testergebnisse (``fehlerhaft'' oder ``intakt'') zu dem zentralen Kontrolleur, dessen Aufgabe ist, die defekten Prozessoren aufgrund der vom System erzeugten Testergebnisse zu identifizieren.
Die intakten Prozessoren geben richtige Testresultate aus.
Die Ergebnisse der fehlerhaften Prozessoren sind unzuverlässig.
Alle Fehler sind permanent.
Ein System $ S$ heißt (sequentiell) $ t$ -diagnostizierbar, wenn mindestens ein fehlerhafter Prozessor identifiziert werden kann, vorausgesetzt, dass ihre Gesamtzahl $ t$ nicht überschreitet.

Diagnostizierbarkeit

$ t(G)\ :=$ Maximum $ t$ , so dass das System $ t$ -diagnostizierbar ist.

Diagnose Probleme
1) Für einen gegebenen Graphen $ G$ bestimme oder schätze $ t(G)$ ab (graphentheoretisches Problem).
2) Finde effiziente Algorithmen für Fehler Diagnose.

In [P29] geben wir einen Diagnosealgorithmus $ A$ an, der für beliebige zusammenhängende Graphen $ G=(V,E),\ \vert V\vert=N$ angewendet werden kann.

Die Diagnostizierfähigkeit des Algorithmus erfüllt
$ t_A(G)\geq \max \{m(G), 2N^{1/2}-3\}$ .

Die Komplexität des Algorithmus ist $ O(\vert E\vert)$ .

Dies verbessert die Resultate von Khanna/Fuchs (1996): $ \Omega (N^{1/3})$ für beliebige zusammenhängende Graphen, $ \Omega ((N/k)^{1/2})$ für $ k$ -Bäume, $ \Omega (N^{1/2})$ für würfel-zusammenhängende Zykel (cube connected cycles).

Der Algorithmus ist optimal für ``schlechte'' Graphen: Es gibt Graphen (Bäume) mit $ t(G)=2\left \lceil N^{1/2}\right \rceil -3$ .

Für den $ n$ -Würfel haben wir $ t_A(H^n)\geq m(H^n)>\binom n{\lfloor n/2 \rfloor}$ .

Ist die Anzahl der Fehler $ t\leq \binom n{\lfloor n/2 \rfloor}$ , dann kann der Status von mindestens $ 2^{n-1}+\binom {n-1}{\lfloor (n-1)/2 \rfloor}$ Prozessoren durch den Algorithmus identifiziert werden.

Obere Schranke: $ t(H^n)=O(2^n/n^{1/4})$ .

Frühere beste untere Schranke: $ t(n)=\Omega (2^n\log n/n)$
Khanna/Fuchs (1996), Caruso/Chessa/Maestrini/Santi (2002)

Friedman (1975) führte den Begriff der $ t\vert s$ -Diagnose ein. Ein System wird $ t\vert s$ -diagnostizierbar genannt, wenn alle fehlerhaften Einheiten in einer Menge von höchstens $ s$ Einheiten isoliert werden können, vorausgesetzt die Zahl der fehlerhaften Einheiten übersteigt nicht $ t$ .

Die Motivation für diese Diagnose Strategie (auch pessimistische Diagnose Strategie genannt) ist es, die Diagnostizierbarkeit eines Systems zu erhöhen (im Bezug auf die Ein-Schritt Diagnose Strategie) und gleichzeitig das Delay zu verringern (der Nachteil einer sequentiellen Diagnose Strategie) bei der Fehleridentifikation in den Großrechnersystemen.

Sei $ r\geq 0$ , der Grad eines Systems ist das maximale $ t$ für das es $ t\vert t+r$ -diagnostizierbar ist.

Den Grad der Diagnostizierbarkeit eines Systems festzustellen (bei gegebenem $ r$ ) ist sogar eine schwierige Aufgabe für Systeme mit einer regelmäßigen Topologie. Chwa und Hakimi (1981) charakterisierten die $ t\vert t$ -Diagnostizierbarkeit und gaben einen leistungsfähigen Diagnosealgorithmus für solche Systeme an. Kavianpour und Kim (1991) zeigten, dass der Grad der $ t\vert t$ -Diagnostizierbarkeit des $ n$ -dimensionalen Würfels $ 2n-2$ für $ n\geq 4$ ist. In [P30] ermitteln wir den Grad der $ t\vert t+r$ -Diagnostizierbarkeit des $ n$ -dimensionalen Würfels $ t(n,r)$ für $ 0\leq r\leq 2n-4$ .

Theorem.

(i)
Für $ 0\leq r\leq n-2$ und $ n\geq 4$ gilt $ t(n,r)=\binom n2-\binom{n-r-2}2+1$ .
(ii)
Für $ n-1\leq r\leq 2n-4$ und $ n\geq6$ gilt $ t(n,r)=\binom n2+\binom{n-2}2-\binom{2n-4-r}2+1$ .

Wir beschreiben auch einen einfachen Algorithmus für die $ t\vert t+r$ -Diagnostizierbarkeit im $ n$ -dimensionalen Würfel, wobei $ 0\leq r\leq 2n-4$ . Der Algorithmus hat lineare (in der Anzahl der Kanten) Komplexität und kennzeichnet die fehlerhaften Einheiten in einer Menge (von höchstens $ t+r$ Einheiten), die höchstens $ r+1$ fehlerfreie Einheiten enthält.

In Kooperation mit dem DFG-Projekt ``Informationstheorie und Kombinatorik'' wurden Suchmodelle mit verschiedenen Fehlerkonzepten betrachtet. Das Rényi-Berlekamp-Ulam Spiel ist ein klassisches Modell zur Bestimmung der Mindestanzahl von Fragen, um eine unbekannte Zahl in einer Menge $ \mathcal U$ zu finden, wenn eine begrenzte Anzahl der Antworten fehlerhaft ist. Wir haben über Arbeiten zu diesem Problem im Fortsetzungsantrag 2003 berichtet. Durch die Einführung neuer Fehlertypen ist es uns gelungen, wie im Antrag 2003 als Ziel formuliert, das Spiel für weitere Restriktionen zu lösen.

In der Variante, die wir in [P33] betrachten, werden Fragen mit $ q$ vielen möglichen Antworten gestellt, die Lügen werden durch einen gewichteten bipartiten Graphen bewertet und eine begrenzte Zahl von Lügen mit Gesamtgewicht $ e$ ist erlaubt. Wir geben eine scharfe asymptotische Schranke für die Anzahl der Fragen an, die benötigt werden, um das Problem zu lösen. Unsere Resultate sind konstruktiv. Die Strategie besteht aus $ \log \vert\mathcal U\vert-\lceil {e\over w}\rceil$ adaptiven Fragen ($ w$ ist das minimale Kantengewicht ungleich Null) und dann, nur abhängig von den Antworten zu diesen Fragen, einem Bündel von Fragen. In [P31] geben wir eine optimale Strategie in zwei Stufen für den ungewichteten Fall an (alle Kanten haben Gewicht 1).

In [P32] leiten wir eine obere und eine unterere Schranke für die Rate eines nichtbinären fehlerkorrigierenden Codes mit Rückkopplung her. Die Schranken stimmen für große Raten überein. Dies sind Verallgemeinerungen der Schranken von Berlekamp, Schalkwijk und Zigangirov im binären Fall.

Wir konnten auch zeigen, dass die Hammingschranke eine obere Schranke für $ q$ -äre fehlerkorrigierende Codes mit Rückkopplung und lokalisierten Fehlern ist. Offensichtlich ist diese Grenze für den binären Fall ($ q=2$ ) scharf.


4. Monotonicity Testing and Property Testing


Das ``Monotonicity Testing'' ist ein Sortierproblem, das wie folgt definiert wird:

Gegeben sei eine (endliche) partiell geordnete Menge $ P$ versehen mit einer unbekannten reellwertigen Funktion $ f$ . Man finde heraus, ob diese Funktion monoton wachsend ist, d.h. ob $ f(x)\le f(y)$ für alle $ x<y$ in $ P$ .

In [P35] studieren wir das ``worst case'' Verhalten von ``Monotonicity Testing'' Algorithmen. Diese Untersuchungen wurden schon in den Zielen des Fortsetzungsantrags 2003 angekündigt.

Zwei Modelle werden betrachtet: das Vergleichsmodell und das lineare Modell.

Ein eher überraschendes Resultat für das Vergleichsmodell ist das

Beispiel einer teilweise geordneten Menge (Poset) mit 9 Elementen und strikt kleinerer ``monotonicity testing'' Komplexität als einige ihrer Subposets.

Der Beweis ist schwierig und nimmt 20 Seiten ein.

Ein anderes interessantes Resultat (für das Vergleichsmodell) ist das

Theorem 1. Wenn eine Poset $ P$ in Subposets $ P_1,\dots,P_\ell$ partitioniert werden kann mit $ x<y$ für $ x\in P_i$ und $ y\in P_j$ für $ i<j$ und $ x$ ist mit $ y$ unvergleichbar, falls $ i=j$ , dann hat die Poset $ P$ folgende ``monotonicity testing'' Komplexität:

$ C(P)=\sum^{\ell-1}_{i=2}\left\lceil\frac32n_i\right\rceil +n_1+n_\ell-\ell+1$ , wobei $ n_i=\vert P_i\vert,i=1,\dots,\ell$ .

Aus dem Resultat folgt, dass die Komplexität zur gleichzeitigen Feststellung, ob in $ (S_1, \dots, S_n)$ , $ S_1$ das Minimum und $ S_n$ das Maximum ist, den Wert $ \left\lceil\frac{3n}2\right\rceil-3$ hat.

Yao (1975) (siehe auch Aigner ``Combinatorial Search'', Kapitel 4, 1988) fragte nach der Komplexität des simultanen Findens des Minimums und des Maximums in einer Folge von $ n$ reellen Zahlen im linearen Modell.

Eine neue unterere Schranke wird für diese Komplexität hergeleitet.

Theorem 2. Um das Maximum und das Minimum in einer Folge von $ n$ reellen Zahlen gleichzeitig zu finden benötigt man mindestens 1.168$ n$ lineare Vergleiche für genügend große $ n$ .

Alle Ergebnisse und der Stand der Forschung werden ausführlich in der Arbeit [P36] dargestellt.


III Vorhersagetheorie in Netzwerken


Lars Bäumer, dessen Dissertation Vorhersagetheorie in Verbindung mit Identifikation behandelte, hat nicht wie bei der Antragsstellung geplant an diesem Projekt mitgearbeitet, da er mein Forschungsprojekt am Zif als Assistent unterstützt.

Er hat sich dort biologischen Fragestellungen zur Evolution von Sprachen und zur Tierkommunikation gewidmet. Vorhersagetheorie wurde deshalb in diesem Projekt nicht betrieben. Die BAT IIa-Stelle dieses Projektes hatte durchgehend Harout Aydinian inne.


IV Zwischenspeicher Managementstrategien in Netzwerken und Creating Order

Christian Wischmann wird dieses Thema in seiner Doktorarbeit behandeln. Seine ersten Ergebnisse präsentierte er auf dem Jahreskolloquium in Aachen 2006.


Weitere Literaturhinweise im Ergebnisbericht