ZiF Logo

General Theory of Information Transfer

Opening Conference


ZiF Research Year


November 4 - 9, 2002


with two days devoted to the memory of


Levon Khachatrian


(Abstracts$^1$)


R. Apfelbach, U. Schmidt and N.Yu. Vasilieva: Chemical Information Transfer in Phodopus Hamsters

Dwarf hamsters of the genus Phodopus live in social groups. Laboratory observations of P. campbelli and P. sungorus suggested that these hamsters are monogamous. However, field research provided evidence that the mating system of at least P. campbelli is promiscuous, with males and females mating with multiple partners. The territorial structure is represented by widely overlapping home ranges (up to 16 ha in area) in males and little overlapping in females. Population density throughout the ranges is usually low. The role of chemical signals provided by various secretions seem very important for the maintenance of the social structure (Phodopus hamsters discriminate individuals via scent marks), for orientation within the home range and - as we suspected - to retrieve hidden food.

Our hypothesis was based on the observation that both species have a unique scent organ, the so called supplementary sacculi at the opening of the cheek pouches. When foraging hamsters collect food items in their cheek pouches and transport them to cooperative food caches. The transported food comes in contact with the strong smelling secretion from the sacculi and thus becomes odor marked. When searching for the cached food, the deposited scent might help guide the searching animal to the hidden food. To addres this hypothesis, we conducted behavioral tests using food marked with saccular secretions of different individuals. In addition, we conducted chemical analysis (Headspace-GC/MS) of the secretions from different individuals of both species in order to identify their volatile components, which we then used in behavioral tests.

Chemical analyses of odorous substances in the secretions showed the same qualitative composition for all tested individuals of both species. The substances found were: Acetic acid, Butyric acid, Isobutyric acid, Isovaleric acid, Valeric acid and Phenol. The pure substances did not release orientation reactions in any species. Analyses of behavioral experiments with complete secretions yielded remarkable behavioral differences between the two species. When simultaneously exposed to marked and unmarked food, P. campbelli oriented to and preferred food which was scented with the secretion of its own species over the secretion of the other species. P. sungorus, however, did not make use of olfactory signals when retrieving hidden food as secretions of either species did not influence orientation. We, therefore, conclude that in P. campbelli the secretion of the sacculi guides the searching animal; small variations in relative quantities of all six components seem to be the base for differentiation among secretory substances of different species and possibly of individuals. In contrast, when searching for cached food P. sungorus does not use odor cues but a different searching strategy like e.g. path integration.

A. Apostolico: Bearable Monotonies of Surprise

The discovery on a massive scale, of recurrent sequence patterns such as substrings or motifs and related associations or rules is ubiquitous to current applications of computing and poses interesting methodological and algorithmic problems. We discuss scenarios in which the need to succinctly compute, store, and display interesting or unusual patterns can overcome the inherently unbearable size of the implied tables and synopses.


E. Arikan: An information-theoretic analysis of Grover's algorithm (see [B22])


S.V. Avgustinovich, A.Yu. Vasil'eva: Testing sets for 1-perfect codes (see [B56])


V. Balakirsky: Estimates of the bit error probabilities for linear block codes and symmetric binary-input memoryless channels

A coset representation of the bit error probabilities for binary linear block codes and arbitrary symmetric memoryless channels is presented. Such a representation leads to simple upper bounds on the bit error probabilities for code components expressed via $2n$ code spectra, where $n$ is the code length, and to a ''bounded distance decoding'' algorithm.


V. Batagelj: Efficient Algorithms for Citation Network Analysis

In a given set of units ${\mathbf{U}} $ (articles, books, works, ...) we introduce a $citing$ relation $R \subseteq {\mathbf{U}} \times {\mathbf{U}} $

\begin{displaymath}u R v \equiv v \mbox{ cites } u \end{displaymath}

which determines a citation network ${\mathbf{N}} = ({\mathbf{U}} ,R)$. A citing relation is usually irreflexive and (almost) acyclic.

The citation network analysis started with the paper of Garfield et al. (1964) [4]. The next important step was made by Hummon and Doreian (1989) [5]. They proposed three indices (NPPC, SPLC, SPNP) - weights of arcs that provide us with automatic way to identify the (most) important part of the citation network - the main path analysis.

In this paper we make a step further. We show how to efficiently compute the Hummon and Doreian's weights, so that they can be used also for analysis of very large citation networks with several thousands of vertices. Besides this some theoretical properties of the Hummon and Doreian's weights are presented. The nonacyclicity problem in citation networks is discussed.

The proposed methods are implemented in Pajek - a program, for Windows (32 bit), for analysis of large networks. It is freely available, for noncommercial use, at its homepage [3]. Some analysis of the citation networks obtained from the Eugene Garfield's collection of citation data [6] produced from the WebofScience www.isinet.com are also presented.
Keywords: citation network, main path analysis, arc weight, algorithm, acyclic

[1]
Asimov I.: The Genetic Code, New American Library, New York, 1963.
[2]
Batagelj V.: Some Mathematics of Network Analysis. Network Seminar, Department of Sociology, University of Pittsburgh, January 21, 1991.
[3]
Batagelj V., Mrvar A.: Pajek - program for analysis and visualization of large networks.
http://vlado.fmf.uni-lj.si/pub/networks/pajek/
[4]
Garfield E, Sher IH, and Torpie RJ.: The Use of Citation Data in Writing the History of Science. Philadelphia: The Institute for Scientific Information, December 1964.
http://www.garfield.library.upenn.edu/papers/
        useofcitdatawritinghistofsci.pdf
[5]
Hummon N.P., Doreian P.: Connectivity in a Citation Network: The Development of DNA Theory. Social Networks, 11(1989) 39-63.
[6]
Pajek's datasets - citation networks:
http://vlado.fmf.uni-lj.si/pub/networks/data/cite/


G. Bérczi: On finite pseudorandom sequences of k symbols

In earliar papers C.Mauduit and A.Sárközy have introduced and studied the measures of pseudorandomness for finite binary sequences. In [8] they extend this theory to sequences of k symbols: they give the definitions and also construct a ``good'' pseudorandom sequence of k symbols. In this paper these measures are studied for a ``truely random'' sequence.


C. Bey: Remarks on an edge-isoperimetric problem

Among all collections of a given number of $k$-element subsets of an $n$-element groundset find a collection which maximizes the number of pairs of subsets which intersect in $k-1$ elements.

This problem was solved for $k=2$ by Ahlswede and Katona, and is open for $k>2$.

We survey some linear algebra approaches which yield to estimations for the maximum number of pairs, and we present a new and short proof of the Ahlswede-Katona result.


R.Ahlswede, V.Blinovsky: Large Deviations in Quantum Information Theory

We obtain the asymptotic estimations of the probabilities of events of special types which are usefull in quantum information theory .


Let $H_d$ be the space of Hermitian $d\times d$ matrices and $P_d$ be a distribution on it. One of the interesting for quantum information theory problems is the estimating the probability of the event (see [2])

\begin{displaymath} B_n (C) =\{ Z=\sum_{i=1}^{n}Z_i \not\leq nC \} , \end{displaymath} (1)

where $\{ Z_i \}$ is a sequence of i.i.d. random Hermitian matrices of finite dimension $d\times d$ and $C$ is some Hermitiam matrix. Then we also consider the case when $Z_i$ is random Hilbert-Schmidt operator on infinite dimensional separable Hilbert space ${\cal H}$.

Let's consider for a moment that the sequence $P_n$ is exponentially compact. It is easy to see that the sets $B_n (C)$ are Borel (actually they are open). Next we prove that if

\begin{displaymath} EZ_i \leq C \end{displaymath} (2)

then
  $\textstyle -$ $\displaystyle \inf_{x\in R^d}\lim_{\epsilon\rightarrow 0}\Lambda' (C-I\epsilon ,x)\leq\liminf_{n\rightarrow\infty}\frac{\ln P_n (B_n (C))}{n}\leq$ (3)
  $\textstyle \leq$ $\displaystyle \limsup_{n\rightarrow\infty}\frac{\ln P_n (B_n (C))}{n}\leq -\inf_{ x\in R^d}\Lambda' (C,x) ,$  

where

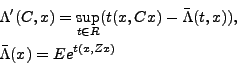
\begin{eqnarray*} &&\Lambda' (C ,x)=\sup_{t\in R}(t(x,Cx) -\bar{\Lambda}(t,x)),\\ && \bar{\Lambda} (x)=Ee^{t(x,Zx)} \end{eqnarray*}


and $I $ is unit matrix. Note that it is enough to optimize the expressions in the last relations only over unit vectors $x\in R^d$. Note that if the relation (2) is not valid, then

\begin{displaymath} \lim_{n\rightarrow\infty}\frac{\ln P_n (B_n (C))}{n} =0. \end{displaymath}

Next we consider the case when $d=\infty$ and we consider the matrices, which corresspond to self-adjoint Hilbert-Schmidt operators on Hilbert space $\cal H$. In finite dimension the sequence $P_n$ is compact. In the case $d=\infty$ we should make additional coditions on the distribution $P$. Hence we should find in which cases this assumption is valid. The exponential tightness of the sequence $P_n$ is a consequence of the following condition. Let $b=\{ b_1 ,b_2 ,\ldots ,b_n ,\ldots ,\}$ be some $\ell_2 -$ sequence and $Z= (z_{i} )$ be $R^\infty$- representation of self-adjoint H-S matrix $Z$. If for some natural $n$ the sum
\begin{displaymath} \pi_n=\sum_{i=1}^{\infty}\left(e^{-\Omega^+_i n (b_i )}+e^{-\Omega^-_i n (b_i )}\right) \end{displaymath} (4)

where
\begin{displaymath} \Omega^\pm_i (b)=\sup_{t\in R}((t ,Ex_i \pm \vert b\vert)-\ln Ee^{(t,z_i )}), \end{displaymath} (5)

converges, then the sequence $P_n$ is exponentially compact. Note that the lhs of inequality (4) is nothing else but the additive upper bound for the probability that $\vert Ez_i -z_i \vert>\vert b_i \vert$ for some $i$. Note that even if one considers the diagonal matrices ${\cal A}$ and distribution $P$ on them (all elements on the diagonals of matrices from ${\cal A}$ are $\ell_2 -$sequences) and we don't know the joint distribution of different diagonal elements the only possible upper bound for the probability $P(\vert Z^n -EZ^n \vert\not\leq Cn)$ where $C$ is some self-adjoint H-S matrix is the additive bound (4), which can be obtained by using the Chebyshev inequality for the estimation of deviations $P(\vert z_j -Ez_j \vert>c_j n)$. Hence in this case condition (4) is also necessary to obtain the nontrivial upper bound on the probability of the event $\vert Z^n-EZ^n \vert\not\leq Cn$.

Also, we derive the convinient upper asymptotic bound on the probability of the event $Z^n\not\leq Cn$ which follows from our considerations. We use the Chebyshev estimation ($x$ is unit vector)


\begin{displaymath} \limsup_{n\rightarrow\infty}\frac{P_n (B_n (C))}{n}\leq \ln \vert\vert E^{tZ_j -tC}\vert\vert. \end{displaymath}

This formula in finite dimensional case was obtained in [2].

[1]
J.D. Deuschel and D.W. Strook, Large deviations, Academic press, Boston, 1989.
[2]
R. Ahlswede and A. Winter, Strong Coverse for Identification via Quantum Channels, Transactions IT, vol. 48, no. 3, 559-579, 2002.
[3]
M. Reed and B. Simon, Functional analysis, Academic Press, V. 1,2, New York and London, 1972.


S. Csibi, E.C. van der Meulen: Huge-size codes for identification via a multiple access channel under a word-length constraint

It is well known from pioneering papers published from 1989 on that, for identification via a communication channel of given Shannon Capacity, the size $N(n)$ of such codes might grow (asymptotically) doubly-exponentially with the word length $n$, as $n\to\infty$. (This might be so, provided the transmission of the identifier is not confined to being placed into the heading of the message content.) - The main subject of the present paper are further contributions to the study of such codes under some given word length constraint $n\leq n_0$ for identification via a given simple kind of noiseless multiple access channel (MAC). More distinctly, a MAC will be considered in this paper, controlled by the very same single close to least length cyclically permutable sequence at all network nodes involbed. While the false identification probability $P$ (false) $(n)$ at $n<n_0<\infty$ does no more vanish under such a constraint, fortunately this probability might be drastically suppressed both by serial and parallel versions of an approrpiate (non-algebraic) error control (FEC), well-defined in the paper. A novelty of the present paper is proving exactly the huge size of an asymptotically optimal identification code sequence under given word length constraint $n\leq n_0$ (with and without a non-algebraic FEC). (This result has been mentioned at the Preparatory Session of the same Res. Gr. at ZiF, Uni. Bielefeld in Feb., 2002, still as a conjecture. See the footnote.) - Huge size identifier sets might be of design interest any time certain perspective remote alarm services of much interest are considered, relying upon global geographic positioning. We have in mind occasional alarms to be conjeyed via a simple multiple access channel, being controlled by the same single common cyclically permutable sequence at all nodes involved, and being appropriately embedded into an otherwise conventional public mobile cellular wireless network. It will be pointed out, under what circumstances the use of huge identification codes might be worth further detailed investigation by designers interested in such perspective services.


I. Csiszar, P. Narayan: The Secret Key Capacity for Multiple Terminals

We consider the problem of characterizing the secret key (SK)-capacity [1, 2, 3] for an arbitrary number of terminals, each of which observes a distinct component of a discrete memoryless multiple source, with unconstrained public communication allowed between these terminals. Our main contribution is the determination of SK-capacity for an arbitrary subset of terminals with the remaining terminals serving as ``helpers'', when an eavesdropper observes the communication between the terminals but does not have access to any other information. We also determine the private key (PK)-capacity when the eavesdropper additionally wiretaps some of the helper terminals from which too the key must then be concealed.

[1]
U.M. Maurer, Secret key agreement by public discussion from common information, IEEE Trans. Inform. Theory, Vol. 39, 733-742, 1993.

[2]
R. Ahlswede and I. Csisza'r, Common randomness in information theory and cryptography, part I; Secret sharing, Trans. Inform. Theory, Vol. 39, 1121-1132, 1993.

[3]
I. Csiszar and P. Narayan, Common randomness and secret key generation with a helper, IEEE Trans. Inform. Theory, Vol. 46, 344-366, 2000.


C. Deppe: An upper Bound for the binary channel with feedback and a fixed number of errors

We consider the binary channel with noiseless feedback and fixed number of errors. We derive an upper bound for the number of bits needed if the number of errors is fixed and the number of messages is large enough. We improove an upper bound of Spencer by generalizing our result for $l=3$. The result can be formulated in an equivalent way for the Renyi-Ulam Game.


J. Dittmann: Invertible Watermarking combined with electronic signatures for image and audio authentication

Multimedia data manipulation has become more and more simple and undetectable by human audible and visual system due to technology advances in recent years. The robust watermarking methods for owner and copyright holder or customer identification are usually not able to detect manipulations on images or audio material and their design is completely different from that of fragile watermarks. Dealing with fragile watermarks, different aspects of manipulation have to be taken into account. The sensitivity of fragile watermarks to modification leads to their use in media authentication. Today we find several fragile watermarking techniques to recognize manipulations. Our contribution focuses mainly on the design of an invertible watermarking scheme combined with digital signatures for high security applications. We present an approach for image and audio data to detect each bit change and reconstruct the original data, where we combine digital signature schemes and digital watermarking to provide a public verifiable data authentication and a reproduction of the original protected with a secret key.


R.D. Dodunekova, S.M. Dedunekov, E. Nikolova: Proper codes: an overview and recent results (see [D2])


A.G. D'yachkov, E.V. Konstantinova: On Entropy and Information of Trees

We consider Shannon's entropy and information of a joint probability distribution generated by the distance matrix of an unoriented tree with $n$ vertices. For chemical applications, a tree represents an alkane molecule and the entropy (information) is a measure of a molecular branching [1, 2]. We investigate some classes of trees and obtain asymptotic ($n\to\infty$) formulas for their information measures.

[1]
D.Bonchev, Information-theoretic indices for characterization of chemical structures, Research Studies Press, Chichester, 1983.

[2]
N. Trinajstic, Chemical Graph Theory, 2nd revised ed; CRC Press, Boca Raton, FL, 1992.


J. Eisert: From reversibility to irreversibility and back again: asymptotic state manipulation in quantum mechanics

This talk will be concerned with the theory of quantum entanglement. The main emphasis will be put on the question of reversibility of asymptotic entanglement manipulation. The first part of the talk will deal with pure quantum states, for which entanglement manipulation with respect to local quantum operations is in fact reversible. For mixed states, in turn, reversibility is lost. Very recent results, however, suggest that reversibility may be regained when one slightly extends the underlying set of quantum operations.


K. Engel: Optimal Multileaf Collimator Field Segmentation for Inverse Radiotherapy Planning

Modern radiotherapy planning algorithms are composed of several routines. There are two essential steps. In the first step a small number of intensity modulated fields are determined with the aim that the planning target area receives homogenously a fixed dose and that regions of interest are protected as good as possible. Here a field depends on several parameters like position of the isocenter, field breadth, field length, energy, collimator rotation, gantry angle, table angle, kind of wedge. Moreover, the intensity of the beam through the rectangle given by field breadth and field length is not homogenous, but modulated, i.e., there is a compensation depending on the point of the rectangle. After discretization this intensity modulation is described by an intensity map which is mathematically an $m \times n$ matrix with nonnegative entries. There are several methods of realizing such an intensity map, but a modern way is the usage of a multileaf collimator that, by means of his leaves, opens and closes certain regions of the rectangle. Several leaf-positions, called segments, must be superposed in order to realize the intensity map. The second essential step in planning algorithms is the determination of a small number of segments (associated with monitor units) which realize the intensity map in small total time.

In our talk we will present a new algorithm for this second step. We only study the static case (stop and shoot) and optimize the total number of monitor units (the total relative fluence, the total shooting-time) and the number of segments. If the leaves may move very quickly these two objectives are most important. We will sketch a short exact proof for a formula giving the smallest total number of monitor units and describe a class of algorithms yielding this minimal value. A special member of this class provides in addition a solution with a very small number of segments.


Z. Füredi and M. Ruszinkó: Large convex cones in hypercubes (see [D14])


S. Galatolo: Information in weakly chaotic dynamical systems

In a topological dynamical system the complexity of an orbit is a measure of the amount of information (measured by algorithmic information content) that is necessary to describe the orbit.

This indicator is invariant up to topological conjugation. The knowledge of these invariants provide more information than the knowledge of the entropy of the system and it can be used to distinguish between systems with equal entropy (mainly between systems with zero entopy).

We consider this indicator of local complexity of the dynamics and provide different examples of its behavior, showing how it can be useful to characterize various kinds of chaotic dynamics.

This indicator of the complexity of the dynamics is also related with initial condition sensitivity and other chaos indicators.

Moreover we can have a numerical estimation of the behavior of these indicators by measuring the information by the use of suitable data compression algorithms.

In the case of 0 entropy we need algorithms which are very efficient in compressing 0 entropy strings.

We performed some experiment and we show that the results are very similar to the teoretical predictions.

M.E. Haroutunian and Evgueni A. Haroutunian: $E$-capacities of Varying Channels

Let ${\cal X}, {\cal Y},{\cal S}$ be finite sets and the transition probabilitites of a discrete memoryless channel with input alphabet ${\cal X}$ and output alphabet ${\cal Y}$ depend on a parameter $s$ with values in ${\cal S}$. In other words we have a set of conditional probabilities

\begin{displaymath} W_s=\{W (y\vert x,s), x\in {\cal X}, y\in {\cal Y} \}, s\in {\cal S}. \end{displaymath}

Values of the parameter $s$ can be changed by different rules, depending on which different definitions of channels can be considered.


P. Harremoës: Testing binomial vs. Poisson distributions using information theoretic methods

The index of dispersion of a sample is defined by

\begin{displaymath} d=\frac{\sum^n_{i=1}(x_i-\bar x)}{\bar x}.\end{displaymath}

The indes of dispersion is the statistics most widely used when testing whether or not a random variable has a Poisson distribution.Using a quotient test is equivalent to using information divergence as statistics. We will prove that the information divergence from the empirical distribution to the Poisson distributionwith mean $\bar x$ is lower bounded by

\begin{displaymath} \frac{(1-\frac dn)^2}4.\end{displaymath}

We will see that in important cases the two statistics will approximately give the same result.


T.F. Havel: Information Dynamics in Open Quantum Systems

It is well-known that the observables of a quantum system may have indeterminate values. The density matrix allows one to combine this intrinsic indeterminacy with ordinary ignorance of the state. This ignorance can be regarded classically, but when the quantum system of interest is part of a larger quantum system including its environment, it can also be explained by the indeterminacy of the observables of the environment. Such systems are called ``open'', and the dynamics of their density matrices can be described by either a stochastic process or by the associated master equation for the density matrix. In this talk I will give a brief overview of the basic ideas behind the theory of open quantum systems and the elegant mathematics that this theory uses. I will then describe some applications of this theory to experiments in nuclear magnetic resonance spectroscopy.


G. Kabatiansky: Hash Codes and Functions: Bounds and Constructions

A notion of hash codes as a generalization of perfect family of hash functions was introduced in [1] and some upper and lower bounds on the cardinality of hash codes/functions were given, among them a very simple upper bound which for many parameters nevertheless is better than the famous Friedman-Komlos bound. In this talk we give a new, recursive bound which is better than the bound from [1] and discuss its relationship with Friedman-Komlos bound.

[1]
L.A. Bassalygo, M. Burmester, A. Dyachkov, and G. Kabatiansky, Hash codes, Proceedings of ISIT-97, Ulm, Germany, 1997.


G. Károlyi: Transversals of Additive Latin Squares

In the first part of this talk I review some results of Levon Khachatrian in combinatorial number theory related to density problems.

In the second part I address the following problem: When does every square submatrix of the addition table of an Abelian group contain a Latin transversal? In other words, given two subsets $\{a_1,a_2,\dots,a_k\}$ and $\{b_1,b_2,\dots,b_k\}$ of an Abelian group, when is it possible to find a permutation $\pi\in S_k$ such that the elements $a_1+b_{\pi(1)},a_2+b_{\pi(2)},\dots,a_k+b_{\pi(k)}$ are all different?

This is obviously true in every ordered Abelian group. Hence, for $k$ fixed, the result can be extended to every finite Abelian group whose order is not divisible by small prime numbers. According to a conjecture of Snevily the result holds in every Abelian group of odd order. Extending a method of Alon, Nathanson and Ruzsa, we verify this conjecture for cyclic groups.


K. Kobayashi, H. Morita, M. Hoshi: Percolation on k-ary Tree (see [B36])


E.V. Konstantinova, M.V. Vidyuk: Information indices and their discriminating power

In this paper we consider the information indices based on the distance in a molecular graph with respect to their discriminating power. The numerical results of discriminating tests on 1443032 polycyclic graphs and 3473141 trees are given.


G. Kyureghyan: Minimal Polynomials of the Modified de Bruijn Sequences (see [D16])


M. Kyureghyan: Complexity of monotonicity checking (see [B44])


M. K. Kuregyan: Recurrent Methods for Constructing Sequences of $N$-polynomials over $F_{2^s}$ (see [D17])


V.I. Levenshtein: Combinatorial problems motivated by comma-free codes

The paper ``Comma-free codes'' by Golomb, Gordon, and Welch (1958) opened a new direction in coding theory: investigation of combinatorial problems of word synchronization for block codes. In the talk some known and new results as well as open problems are discussed in the following directions: comma-free codes, comma-free sequences or difference systems of sets, and codes without overlaps. In particular, the problem on the maximum number of pairwise comparable vectors of a given length over alphabet 0,1,* is considered which was appeared in proofs of nonexistence of perfect comma-free codes of even length. Word synchronization of cosets of linear codes with a minimal redundancy gave rise to investigation of perfect different systems of sets which are generalization of cyclic difference sets. Block codes with the zero synchronization delay are called codes without overlaps and characterized by the property: a proper prefix of a codeword is not a suffix of a codeword.


A. Jakoby, M. Liskiewicz, and R. Reischuk: Private Computations in Incomplete Networks

In a distributed network, computing a function privately requires that no participant gains any additional knowledge other than the value of the function. We study this problem for incomplete networks and establish a tradeoff between connectivity properties of the network and the amount of randomness needed. First, a general lower bound on the number of random bits is shown. Next, for every k>1 we design a quite efficient (with respect to randomness) protocol for symmetric functions that works in arbitrary k-connected networks. Finally, for directed cycles that compute threshold functions privately almost matching lower and upper bounds for the necessary amount of randmoness are proven.


G. Cohen, M. Krivelevich, and S. Litsyn: Bounds on Distance Distributions in Codes of Known Size

We discuss the problem of bounding the possible distance distributions of codes given the knowledge of their size and minimum distance. Using the Beckner inequality we derive upper bounds on distance distribution components which are better than earlier known ones due to Ashikhmin, Barg, and Litsyn. As an application of the suggested approach we derive a lower bound on the undetected error probability for an arbitrary code of given size and minimum distance. We also use the new bounds to derive better upper estimates on the covering radius as a function of the code's size and dual distance.

Finally we compare our results to a conjecture by L.Khachatrian about the number of vectors of given weight in a linear subspace of given dimension.


K. Mainzer: Information dynamics in nature and society: an interdisciplinary approach

In the age of information societies, concepts of information are an interdisciplinary task of mathematics and computer science, natural and social science, and last but not least humanities. On the background of the theories of information, computability, and nonlinear dynamics, information processing is analyzed in complex information networks of nature and society. How far can natural evolution be understood by information and computational systems? How far can natural evolution be used as blue-print for technical developments of information systems? Net- and information chaos in the World Wide Web needs new intelligent methods of information retrieval. Understanding complex dynamical systems in nature and society supports an effective management of communication networks. In the age of globalization, our understanding and managing of information processing in complex systems is one of the most urgent challenges towards a sustainable future of information society.

[1]
K. Mainzer, Thinking in Complexity. The Complex Dynamics of Matter, Mind, and Mankind, Springer: Berlin/Heidelberg/New York 3rd edition 1997.

[2]
K. Mainzer, Gehirn, Computer, Komplexität, Springer: Berlin/Heidelberg/New York 1997.

[3]
K. Mainzer, Computernetze und virtuelle Realität. Leben in der Wissensgesellschaft, Springer: Berlin/Heidelberg/New York 1999.

[4]
K. Mainzer, KI Künstliche Intelligenz. Grundlagen und Perspektiven intelligenter Systeme, Wissenschaftliche Buchgesellschaft: Darmstadt 2002.


J.L. Massey: Reed-Muller Codes and Certain Stream Ciphers

The class of stream ciphers considered is that of additive stream ciphers in which the running-key is produced by applying a nonlinear boolean function to the state of a binary maximum-length linear feedback shift register. A simple and novel theory of such steam ciphers will be presented that is based on the cyclic versions of the venerable Reed-Muller codes.

The $\mu^{\rm th}$-order binary cyclic Reed-Muller code of length $n = 2^m - 1$ has minimum distance $d = 2^{m-\mu} - 1$ and dimension $k = {m \choose 0} + {m \choose 1} + \ldots + {m \choose \mu}$. These cyclic Reed-Muller codes are described in an unusually simple manner that makes all their main properties obvious. It is then shown that a running-key generator in which a boolean function of nonlinear order $\mu$ is applied to the state of an $m$-stage binary maximum-length linear feedback shift register is just an unorthodox encoder for the $\mu^{\rm th}$-order cyclic Reed-Muller code of length $n = 2^m - 1$. This observation leads to a very simple and complete characterization of the linear complexities of the running-key sequences that can be produced by such a generator.


C. Mauduit: Measures of pseudorandomness for finite sequences

I will present a survey on recent results concerning pseudorandomness of finite binary sequences. In a series of papers, A. Sarkozy and myself introduced new measures of pseudorandomness connected to the regularity of the distribution relative to arithmetic progressions and the correlations. We analysed and compared several constructions and we gave (jointly with L. Goubin) a method to construct large families of pseudo-random binary sequences based on the Legendre symbol. In a joint work with R. Ahlswede and L. Khachatrian, we defined a measure of complexity for families of binary sequences. We also studied the expectation and the minima of these measures and the connection between correlations of different order.


H. Nagaoka: Hypothesis testing, channel coding and information spectrum in quantum information theory

The information spectrum method was originally begun by Han and Verdu to treat several problems of classical information theory in the most general settings. I would like to talk about recent attemps of M. Hayashi, T. Ogawa and myself to extend the information-spectrum method to the quantum case, which elucidates the deep relation between hypothesis testing and channel coding in quantum information theory.


M.B. Nathanson: Additive number theory and the ring of quantum integers (see also [B25])

Let $m$ and $n$ be positive integers. For the quantum integer $[n]_q = 1+q+q^2+\cdots + q^{n-1}$ there is a natural polynomial addition such that $[m]_q \oplus_q [n]_q = [m+n]_q$ and a natural polynomial multiplication such that $[m]_q\otimes_q [n]_q = [mn]_q$. These definitions lead to the construction of the ring of quantum integers. It is also shown that addition and multiplication of quantum integers are equivalent to elementary decompositions of intervals of integers in additive number theory.

The polynomial multiplication of quantum integers $[m]_q\otimes_q [n]_q = [mn]_q$ leads to the functional equation $f_m(q)f_n(q^m) = f_{mn}(q)$, defined on a given sequence $\{f_n(q)\}_{n=1}^{\infty}$ of polynomials. This talk contains various results concerning the construction and classification of polynomial sequences that satisfy the functional equation, as well open problems that arise from the functional equation.

Some related combinatorial problems in additive number theory will also be discussed.


J.L. Nicolas: Sets of parts such that the partition function is even

Let ${\cal A}$ be a set of positive integers. Let us denote by $p({\cal A}, n)$ the number of partitions of $n$ with parts in ${\cal A}$. While the study of the parity of the classical partition function $p({\cal N},n)$ (where ${\cal N}$ is the set of positive integers) is a deep and difficult problem, it is easy to construct a set ${\cal A}$ for which $p({\cal A}, n)$ is even for $n$ large enough : as explained in a paper of I.Z. Ruzsa, A. Sárközy and J.-L. Nicolas published in 1998 in the Journal of Number Theory, if ${\cal B}$ is a subset of $\{1,2,\ldots,N\}$, there is a unique set ${\cal A}={\cal A}_0({\cal B},N)$ such that ${\cal A}\cap\{1,2,...,N\}={\cal B}$ and $p({\cal A}, n)$ is even for $n>N$.

Let us denote by ${\sigma}({\cal A},n)$ the sum of the divisors of $n$ belonging to ${\cal A}$. We have proved, with F. Ben Saïd, that, for any $k\ge 1$, the sequence $({\sigma}({\cal A},2^kn))_{n\ge 1} \bmod 2^{k+1}$ is periodic. From this result, we can deduce the standard factorization into primes of the elements of ${\cal A}={\cal A}_0({\cal B},N)$. The case ${\cal B}=\{1,2,3\}$, $N=3$ will be explicited. Moreover, it is possible to show that the number of elements of ${\cal A}_0(\{1,2,3\},3)$ up to $x$ is asymptotically equivalent to ${\displaystyle} c\frac{x}{(\log x)^{3/4}}$, where $c=0.9371832387\ldots$

At the end, some open questions on this topics will be presented.

A. Barg and D. Nogin: Bounds on packings of spheres in the Grassmann manifold

We derive the Gilbert-Varshamov and Hamming bounds for packings of spheres (codes) in the Grassmann manifolds over reals and complex numbers. Asymptotic expressions are obtained for the geodesic metric and projection Frobenius (chordal) metric on the manifold.


R. Eres, G. Landau, and L. Parida: Using Permutation Patterns in Bioinformatics

Genes that appear together consistently across genomes are believed to be functionally related: these genes in each others neighborhood often code for proteins that interact with one another suggesting a common functional association. However, the order of the genes in the chromosomes may not be the same. In other words, a group of genes appear in different permutations in the genomes.

Domains are portions of the coding gene (or the translated amino acid sequences) that correspond to a functional sub-unit of the protein. Often, these are detectable by conserved nucleic acid sequences or amino acid sequences. The conservation helps in a relative easy detection by automatic motif discovery tools. However, the domains may appear in a different order in the distinct genes giving rise to distinct proteins. However, they are functionally related due to the common domains.

This has been earlier addressed as the problem of finding common intervals in multiple permutations. Here, we generalize this problem as a discovery problem called the $\pi$-pattern problem. We explore the different variations of this problem in a practical setting. We next introduce a notation that reduces the number of valid patterns from $O(n^2)$ down to $O(n)$ without any loss of information, making it easier to study the results of the algorithm. We will conclude by showing some results on E Coli data.


V.V. Prelov and E.C. van der Meulen: Optimal covering of ellipsoids with balls in the Hamming space.

An ellipsoid $E_{a}(y,r)$ of shape $a$, radius $r$, and center $y$ in an $n$-dimensional Hamming space $E^{n}\stackrel{def}{=}\{0,1\}^{n}$ is defined as the set of binary vectors $x=(x_{1},\ldots,x_{n}),\;x_{i}\in\{0,1\},\;i=1,\ldots,n$, of length $n$ which satisfy the inequality $d_{a}(x,y)\leq r$, i.e.,

\begin{displaymath} E_{a}(y,r)=\{x\,\in E^{n}\,\vert\,d_{a}(x,y)\,\leq r\}, \end{displaymath}

where

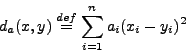
\begin{displaymath} d_{a}(x,y)\stackrel{def}{=}\sum_{i=1}^{n}a_{i}(x_{i}-y_{i})^{2} \end{displaymath}

is the $a$-weighted distance, $a=(a_{1},\ldots,a_{n})$ is a nonzero vector with $n$ real-valued, ordered components $ a_{1}\geq...\geq a_{n}\geq 0$, and $y$ is a fixed vector in $E^{n}$. For $a=(1,\ldots,1)$, we obtain a ball, which will be denoted as $E(y,r)$. 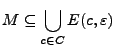Given an integer $\varepsilon>0$, we say that the set of balls $E(c,\varepsilon),\,c\in C\subseteq E^{n}$, forms $\varepsilon$-covering of a set $M\subseteq E^{n}$ if $M\subseteq\displaystyle\bigcup_{c\in C}E(c,\varepsilon)$. The $\varepsilon$-entropy $H_{\varepsilon}(M)$ of a set $M\subseteq E^{n}$ is defined as the logarithm of cardinality of the minimal $\varepsilon$-covering of the set $M$.

The main goal of this lecture is to present a short survey of recent results in the asymptotic investigation of the $\varepsilon$-entropy $H_{\varepsilon}(E_{a}(y,r))$ of ellipsoids $E_{a}(y,r)$ as the dimension $n$ of the Hamming space tends to infinity. The special case of such ellipsoids whose coefficients $a_{i}$ take only two different values is considered in more detail.


R. Reischuk: Online Algorithms - The Power of Knowledge when Accessing Data

In many situations a bunch of individual tasks are given one after the other as an online sequence, where each task should be executed as fast as possible. Typical examples are scheduling problems in a variety of different settings like server allocations. To guarantee an optimal solution in most cases it is necessary to know the complete sequence in advance. The competitive analysis of online algorithms, which have no knowledge about the future, measures how much performance is lost in comparison to such an ideal situation of complete information.

In this talk we consider the problem to access data in a multi-cash parallel machine environement coherently. After a processor has updated a data item cashed copies in other processors' fast memory cannot be used any longer. In spite of such invalidations we still want to use the limited capacity of each cash optimally to speedup the computation.

For the analysis of this problem, in particular to prove lower bounds, a mathematical model of knowledge states is introduced. They represent the different configurations of local knowledge of each processor. Then the amount of information transfer can be measured by defining appropriate potential functions. By this approach we can determine the competitive ratio exactly for small number of processors.


Z. Reznikova and Boris Ryabko: Applying ideas of information theory to study animal communicative and cognitive skills

At least three main approaches to a problem of animal ``languages'' and intelligence have been applied recently. First, a direct dialog with animals based on language-training experiments. The second approach is aimed at direct decoding of animal signals. The third, principally new, approach to study animal ``language'' has been suggested basing on ideas of Information Theory (see Complexity, 1996, 2,2: 37-42; From Animals to Animats 6, The MIT Press, 2001: 501-506). The main point is not to decipher signals but to investigate just the process of information transmission by measuring time duration, which the animals spend on transmitting messages of definite lengths and complexities.

The first series of laboratory experiments was based on using the maze `` binary tree''. Red wood ants had to transmit each other information quantitatively known to the experimentalist in order to obtain food. This information concerned the sequence of turns toward a trough of syrup. The number of bits necessary to choose the correct way was equal to the number of forks. This allowed the presence of potentially unlimited numbers of messages in ant ``language'' to be demonstrated and estimates of the rate of the information transmission to be made.

To reveal counting and number related skills, we used another sort of a ``tree'' suggesting the ants to transmit information on the number of objects. The experimental set-ups consisted of a «tree trunk» with branches that ended in empty troughs, except for one which was filled with syrup. To start the experiment, an ant scout was placed at the randomly numbered trough containing food and then returned to the nest on its own. The duration of the contact between foragers and the scout was measured. Then we removed the scout and the foragers had to search for the food by themselves. The experiments were so devised as to eliminate using an odour trail. It turns out that the ants are able to count within several tens, and transmit this information to their nestmates.

The last set of experiments was based on the same approach and on two main ideas. The first is that in a «reasonable» communication system the frequency of use of a certain message and the length of that message must correlate. The second is that when using a complicated numerical system , one has to add and subtract small numbers. For example, when using the Roman figures , VII = V + II, IX = X - I, etc. In our experiments the ants had to transmit the information about the coordinates of a « branch» situated on a long « trunk ». Each branch ended in an empty trough , except for one filled with syrup . The food was placed on different branches with different frequencies: on the preliminarily chosen, « special » branches an award occured much more frequently than on the others. For example, in 1993 we chose two «special » branches - 10 and 20 on which the food occured with a probability of 1/3 for each of them, while for any of the other 28 branches the probability was 1/84. When the ants had learnt this, they changed the way they transmitted the information about the coordinates of the branch containing food. The time required for transmitting a message « the trough with food is on the branch N 10 » or « N 20 » by the ants considerably decreased , and so did the messages about branches in the vicinity of the « special» ones - 10 and 20. The analysis of the data suggested that the ants used a method of «representing» the numbers similar to the Roman figures, and the « special» numbers ( 10 and 20 in this case) played the same role as the « special» Roman figures V, X, L etc. Thus, the ants seem to be able to add and subtract small numbers.


B.Ya. Ryabko, V.S. Stognienko, and Yu.I. Shokin: A new statistical testing for random numbers and its application to some cryptographic problems

We address the problem of testing the hypothesis $H_0$ that the letters from some alphabet $A= \{a_1,a_2,\dots , a_k \}$ are distributed uniformly (i.e. $p(a_1)=p(a_2)= \dots =p(a_k)= 1/k$) against the alternative hypothesis $H_1$ that the true distribution is not uniform, in the case when $k$ is large. There are many applications in cryptography and other fields where the alphabet size is quite large. Moreover, informally speaking, it will be shown that there exist such problems, for which $k$ should be chosen as large as possible. It is known that the chi-square test and some others can be applied if the sample size is at least $k$. Thus, in a case of large $k$ the implementation of the chi-square test requires a lot of time. Moreover, it is often difficult to obtain such large samples and the chi-square test cannot be applied. The natural question is why the case of large alphabet size $k$ can be interesting. It turns out that there exist such random bit sequences $x_1,x_2,\dots$ which, from the one hand, are very far from truly random and, on the other hand, the distribution of the words $x_1,\dots,x_s, x_{s+1},\dots, x_{2s},\dots, x_{2s+1}, \dots, x_{3s},\dots$ is uniform for relatively small $s$. (We call such bit streams as two-faced processes.) Hence, if a test is designed for two-faced processes testing, it must deal with the relatively large word length. Therefore, the alphabet contains all $s$-bit words and the alphabet size $k$, $(=2^s)$ grows exponentially when $s$ grows.

It is worth noting that two-faced sequences are often met in cryptography. For example, in fact, pseudorandom number generators are designed to generate such sequences. We suggest a new method, which is called the adaptive chi- square test, for testing the hypothesis $H_0$ in case $k$ is large. It is shown that the new test can be applied when the sample size is much smaller than that required for the usual chi- square test.

We also carried out some experiments in addition to a theoretical investigation of the suggested test. Namely, we tested ciphered texts in English and in Russian in order to distinguish them from random sequences. It is worth noting that the problem of recognition of ciphered texts in a natural language is of some interest for cryptology. It turns out, that the suggested test can distinguish ciphered texts from random ones, basing on samples which are essentially smaller than it is required for usual chi-square test.


A. Sárközy: On primitive sequences

A sequence of positive integers is said to be primitive if no element of it divides any other. The study of primitive sequences started around 1934-35 by the papers of Behrend, Davenport and Erdos. Up to 1990 about 20-25 papers (11 of them jointly by Erdos, Sárközy and Szemeredi) were written on this subject, and in the last decade, Ahlswede and Khachatrian (mostly jointly with Sárközy) have written 8-9 further papers on primitivity and related questions. In the talk a survey of the most important results on primitive sequences will be presented.


O. Serra: The Erdos-Turán property for a class of additive basis

Let $A$ be an additive basis of the positive integers, $A+A=N$. Denote by $r_A(x)$ the number of representations of $x$ as a sum of two elements in $A$. An old conjecture of Erdos and Turán says that the function $r_A(x)$ can not be bounded.

The multiplicative version of this conjecture was proved by Erdos in 1964, and a simple proof was given later by Nešetril and Rödl using Ramsey Theory. The arguments in this last proof are adapted to prove the original conjecture for the class of $2$-bounded additive basis.

We say that $A$ is $2$-bounded if there is a function $f$ such that, for each positive integer $n$, there is a pair $x,y\in A$ with $n=x+y$ such that $\vert S(x)\cup S(y)\vert\le f(\vert S(n)\vert)$, where $S(m)$ denotes the set of positive integers appearing in the binary expansion of $m$, $m=\sum_{i\in S(m)}2^i$.

Y.M. Shtarkov: Joint Matrix Universal Coding of Sequences of Independent Symbols

Coding divergences of probability distributions are introduced. A method of joint matrix universal coding for a set of independent symbols with different statistics is proposed and studied. Two methods of multialphabet matrix coding is considered.


F.I. Solov'eva: Steiner triple systems bi-embedded in nonorientable surfaces

Two Steiner triple systems (briefly STS's) of order $n$ are called bi-embedded if they give face 2-colorable triangulation of the complete graph $K_n$ in a surface. It is shown that there exist nonisomorphic bi-embeddings of STS's of any order $n=3$ $({\rm mod} 6)$ in a nonorientable surface.


N. Tokushige: Some results on multiply intersecting families

Let $n,r$ and $t$ be positive integers. A family ${\cal F}$ of subsets of $[n]=\{1,2,\ldots,n\}$ is called $r$-wise $t$-intersecting if $\vert F_1\cap \cdots \cap F_r\vert\geq t$ holds for all $F_1,\ldots, F_r\in{\cal F}$. We will discuss the maximum size of $r$-wise $t$-intersecting Sperner families and $r$-wise $t$-intersecting uniform families. Among others, we show that a $3$-wise $2$-intersecting Sperner family can have at most ${{n-2}\choose{(n-2)/2}}$ subsets if $n$ is even and sufficiently large. Related tools such as a weighted size of a family and a random walk method will be mentioned.


A. Uhlmann: Quantum information transfer from one system to another one (see also [B19])

There is a one-to-one correspondence between the vectors of a bipartite system with Hilbert space ${\cal H}={\cal H}_a\otimes{\cal H}_b$ and the anti-linear Hilbert-Schmidt mappings from ${\cal H}_a$ into ${\cal H}_b$. These maps are induced by a von Neumann measurement (or another intervention) in one of its subsystems, say in the a-system, and they describe what is known as EPR-effect, (``EPR'' in honour of Einstein, Podolski and Rosen): Because a measurement in a physical system, here ${\cal H}_a$, is preparing a new state in every larger system, here ${\cal H}$, it enforces, generically, a state change in every sybsystem of the larger one, i.e., in the case at hand, in ${\cal H}_b$.

Quantum teleportation in a 3-partite system ${\cal H}_a\otimes{\cal H}_b\otimes{\cal H}_c$ transports vectors from the a-system to the c-system according to a composition of two of these anti-linear maps: One map, from $b$ to $c$, is due to a vector of ${\cal H}_b\otimes{\cal H}_c$, the so-called ancillary vector. The other one, from $a$ to $b$, comes from a measurement in ${\cal H}_a\otimes{\cal H}_b$, terminating, with a certain probability, in a vector of ${\cal H}_a\otimes{\cal H}_b$.

Using the composition law it becomes straightforward to consider quantum teleportation within a $(2m+1)$-partite system ${\cal H}_a\otimes{\cal H}_2\otimes\dots$ by distributed measurements in its (1,2)-, (3,4)-,$\dots$ parts, while the ancillary states are chosen in its (2,3)-, (4,5)-,$\dots$ subsystems.

Similarly one can handle EPR-effects with distributed measurements in 2m-partite systems.

There are some remarkable bridges of the formalism to the Tomita-Takesaki theory in its simplest version, i.e. for type I factors.


I. Wegener: On the complexity of black-box search

In the classical algorithmic scenario it is assumed that an algorithm is designed for a specific problem and can use the full knowledge of the problem instance. General randomized search heuristics like simulated annealing and evolutionary algorithms work in the same way for different problems and get knowledge on the problem instance $f : S\to \mathbb{R}$ only via the answers $f (a)$ to queries $a\in S$. A scenario called black-box optimization is presented for this situation. Yao's minimax principle is applied to prove lower bounds on the black-box complexity of some classes of functions.


R. Wilmink: On quantum broadcast channels

Quantum information-theoretic models of secret source-sharing are developed using a general LOCC scheme, i.e. a protocol involving only local operations and classical communication. This is in order to generate a common random key from a shared quantum state at two terminals without allowing an eavesdropper to obtain information about this key. Coding theorems for special separable states are obtained, and bounds to secret key capacity are also derived for more general quantum source states and other models later. In order to prove results for secret source-sharing schemes with a quantum source state also shared with a wiretapper, multi-user systems are studied and the capacity region for the degraded quantum broadcast channel is started to be determined. Using the results of the foregoing chapters, a sufficient bound on the error rate for unconditional security of the BB84 quantum key distribution protocol is proved.


T. Helleseth and V. Zinoviev: On Goethals codes and Kloosterman sums over $GF(2^m)$

Finding the coset weight distribution of the $Z_4$-linear Goethals codes is connected with solving of the nonlinear system of equations over the Galois Field $GF(2^m)$. Solving this system of equations, we express the number of solutions to this system in terms of Kloosterman sums over the Galois field $GF(2^m)$. Using some natural properties of solutions to this system we obtain some new limitations for possible values of these sums. In particular, we find new identities for Kloosterman sums over $GF(2^m)$.