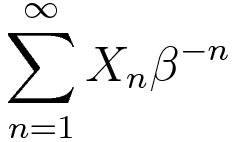Workshop on Dynamical Systems and Aperiodic Order
Bielefeld University, Germany
14th - 17th March 2011
All talks take place in Room V3-201 ("Common Room") in the Bielefeld
University main building.
Click here for
a description of the main building.
Erdős measures revisited
Peter Grabner
Abstract:
Let
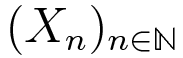
be a sequence of independent random variables
taking values 0 and 1 with equal probability. Erdős in 1939 studied the
distribution of the series
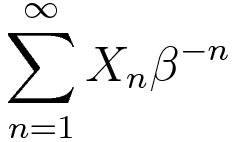
and showed that it is singular continuous, if β is a Pisot number less than 2.
On the other hand B. Solomyak showed in 1995 that the measure is absolutely
continuous for almost all β in the interval (1,2).
Recently, similar measures were encountered in the context of redundant
numeration, for instance in counting the number of base 2 representations
of integers using the digits {0, +/- 1} with minimal number of non-zero digits.
This leads to a generalisation, where the digits are no more independent, but
are governed by a Markov chain. We give an overview over these results.
(Back to Program)
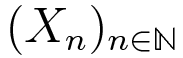 be a sequence of independent random variables
taking values 0 and 1 with equal probability. Erdős in 1939 studied the
distribution of the series
be a sequence of independent random variables
taking values 0 and 1 with equal probability. Erdős in 1939 studied the
distribution of the series