
Two-step projection from N-dimensional space (N=4,6) to 3D and subsequently to 2D produces layer structures that are by construction quasiperiodic in one subspace (2D or 1D) and periodic in its complement (1D or 2D) and periodic in its complement (1D or 2D, respectively).
The final projection produces a plane structure that supports (8 or 12, resp.) fold tilings.
In 1991, M. Dzugutov discovered a new potential [M. Dzugutov, J. Non-Cryst. Sol. 131 (1991) 62] which lead to a dodecagonal quasicrystal if a liquid was cooled slowly enough. Depending on pressure and temperature, there are a number of metastable phases for this interaction.
Here I will report on the behavior of these phases under shock compression. The method employed is molecular dynamics simulations. Depending on the strength of the shock wave and the propagation direction we observe different kinds of phase transitions into close-packed phases as well as into transient structures.
Elastically-dispersive and plastic wave fronts occur during this process. If the shock waves propagate along the three-fold direction in a bcc-crystal additional solitary waves are observed. At elevated temperatures and increased cross-sections the solitary waves get damped. The conditions for the occurance of solitary waves will be discussed.
Main topics:
- Colouring of quasiperiodic patterns with a minimum number of colours
- Tilings in hyperbolic geometry versus quasiperiodic tilings
I looked at different topics of colouring. The theory of colour symmetry in quasiperiodic patterns is well established. The use of colour decoration to define covering clusters has been developed in Greifswald. Another topic is the colouring of patterns with a minimum number of colours. It seems to be interesting to derive aperiodic colourings of periodic patterns. I extended the problem to non-Euclidean space (3D-surface and hyperbolic space).
For a perfect LI-class of quasicrystalline tilings, a corresponding random tiling ensemble can be defined in terms of the cut-and-project-scheme or by suitably relaxed tile matching rules. We explain how to apply the random tiling model to the more general framework of unit-cluster coverings with "fat" overlaps. As an example, we discuss a random covering ensemble of perfect decagon coverings with Penrose-type order.
It this talk I collect data from various experiments and theoretical work. I'll show common features and figure out the differences. Based on these findings I'll propose a new chemical decoration for the model M, which differs from a previous one(1).
(1) G. Kasner, Z. Papadopolos, Kramer, P.: Material Science and Engineering 294-296, pp.355-360 (2001)
In a frame of a geometric icosahedral model we determine the 5, 2 and 3fold bulk terminations to represent the surfaces of i-AlPdMn and i-AlCuFe. Motivated by the bravais rule, of wide validity for crystals, we introduce a maximum density rule(1) for surfaces of quasicrystals.
(1) Z. Papadopolos, P. Pleasants, G. Kasner, V. Fournee, T. Cai, C.J. Jenks, P. Thiel, J. Ledieu, and R. McGrath, preprint cond-mat/0302335
The study of metals deposited on quasicrystalline substrates offers opportunities to derive fundamental physical insights into the processes and energetics involved in formation of an aperiodic-periodic interface. In this talk, examples will be provided of three main types of information, which can be obtained from different coverage (thickness) regimes. With increasing coverage, they are: (i) nucleation; (ii) growth modes, reflecting surface and interface energies; and (iii) crystallographic orientations---specifically, relationships between high-symmetry zone axes of the quasicrystal and the thick crystalline film.
To derive these types of information, we have measured film structures of Ag and Al, as probe metals, on a number of different substrates, including Al(111), the ξ' Al-Pd-Mn approximant, the fivefold surface of icosahedral Al-Pd-Mn, and the tenfold surface of decagonal Al-Ni-Co. Our observations include site-specific "heterogeneous" nucleation on the fivefold quasicrystalline surfaces; strong differences in growth modes for film-surface couples that are chemically similar; and interfacial crystallographic alignments that are different than those reported commonly for confined (bulk) interfaces. Enlightening comparisons can be made between these observations, and those typical of single-element metal homoepitaxy.
The analysed 1D structures were generating as following: the L-bounds of the Fibonacci chain were decorated by nL atoms placed at the positions lj (j=1,nL), the S-bounds were decorated by nS atoms placed at the positions sj (j=1,nS). Using the average unit cell approach the structure factor for such structure reads:

where 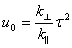 ;
;
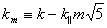 ;
;
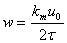
The above structure factor fully describes the diffraction patterns at peaks' positions given by k=k||(n+m/τ), where k|| is the real space scattering vector (k⊥ is the corresponding perp-space component of scattering vector in 2D description of the Fibonacci chain), n and m are the integers indexing the main reflections (n) and their satellites (m). Starting from the diffraction pattern the Patterson function is calculated in physical space. From this function the number of decorating atoms and the relative atomic positions can be collected and used for further structure refinement. For particular decoration and using the above equation one gets very accurate positions of decorating atoms.

Fig.1. Diffraction pattern of the decorated structure with the
following decoration L→llsl and S→sls. In the figure the
diffraction peaks have been connected by the envelope functions
calculated according to the obtained structure factor, for
k0 ≈ 4.55 and different m. Only very weak peaks, with
relative intensities between 0.0035 and 0.06 have been shown.
The defining property of crystals - both periodic and aperiodic - is their essentially discrete diffraction pattern, i.e. consisting of sets of separated Bragg peaks. On the other hand, continous diffraction pattern is specific to the liquids and amorphous materials. There is, however, a big class of materials that are not perfectly crystalline nor perfectly amorphous, e.g. polymers. Diffraction pattern of such materials consists of three components: background, crystalline and amorphous. While one can always cut off the background, the remaining two parts are both equally important, so one cannot neglect any of them.
Classical crystallographic approach is based on the concept of unit cell and reciprocal lattice, therefore its validity is constrained to the analysis of perfectly periodic crystals. If given structure is not of this type, the unit cell doesn't exist and this approach fails. It has been shown [1] that diffraction pattern of such structures may be correctly described in the average unit cell approach based on the reference lattice concept. This approach has been used to calculate diffraction pattern of model one-dimensional structure. By varying some parameters this structure may be set to be more crystalline or more amorphous but always lies somewhere in between. In the limiting cases the diffraction pattern consists of either only Bragg peaks or only continuous part, for "crystalline" and "amorphous" limit respectively.
Numerical calculations have been performed and it turned out that one is able to describe both crystalline (discrete) and amorphous (continuous) component. These components may be easily distinguished as their intensities scale differently with number of atoms N: Bragg peaks scales as N2 while continuous part scales linearly with N. Additionally, it has also been shown that widely used Debye-Waller approximation holds only under very special conditions.
[1] J. Wolny, "The reference lattice concept and its application to the analysis of diffraction patterns", Philosophical Magazine A77, (1998), 395-412
Modulated structures belong to the part of structures with non-periodic arrangement of atoms, which are usually described in higher dimensions. Recently it has been shown that the diffraction pattern of the aperiodic structures can be also described in statistical approach using the average unit cell concept. Definition of the average unit cell is based on the concept of the reference lattice, which is the periodic set of points with periodicity constant equal to λ=2π/k, where k is a given scattering vector. Closest distances between atoms and reference points define the average unit cell Pk(u) for particular wave vector. Fourier transform of such probability distribution gives the structure factor, which describes intensities of periodic series of diffraction peaks.
In this paper we concentrate on the one-dimensional sinusoidally modulated structures where the atomic positions are modulated by the sinus functions. Depending on the value of the modulation vector (q) one obtains commensurately or incommensurably modulated structures. For higher-harmonics modulated structures (e.g. 3q, 5q, and so on) the analysis of diffraction pattern usually becomes very complicated. Using two reference lattices, one for wave vector k and the other one - for wave vector q, the displacements (u and v) of the atomic positions from the nearest reference lattice points can be calculated. The probability distribution of such displacements defines the average unit cell. For complicated structures the parametric representation of the nearest distances u(t), v(t) is recommended. After Fourier transform of the obtained probability distribution one gets the structure factor which fully describes all the peaks in the diffraction pattern, i.e. the main peaks as well as their satellite reflections.
As an example, the sinusoidally modulated structure with 3q modulation of atomic positions has been considered:
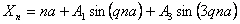 where q=2π/b.
where q=2π/b.
The probability distribution Pkq(u,v) has non-zero value only along a certain line. Projection of that distribution onto u space gives the probability distribution P(u) as following (see also Fig. 1):
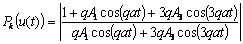
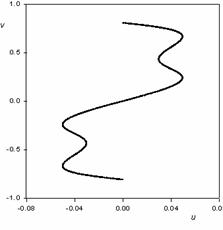
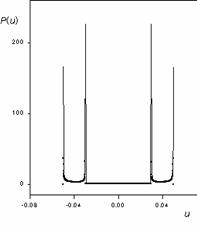
Figure 1a,b. Average unit cell for 3q modulated structures (a) and its
projection to u-parameter space (b). For the calculation it was
supposed: a=1, b=2π, A1=0.05, A3=0.02, and
number of atoms about 100 000.
The Fourier transform of that probability gives the structural factor F. Fourier transform of (2), connects peak's maxima of the main reflections and their satellites. The used approach can be easily extend to the other types of modulations. In this paper the modulation with two incommensurate vectors q1, q2 will be also discussed.
HRTEM investigations of decagonal quasicrystals can be superimposed by tilings, which show different degrees of disorder, intermediant between perfect and random tilings. This and other sources of disorder are assumed to contribute to the entropic stabilisation of quasiperiodic high temperature phases.
Since a strict periodic stacking of random tilings exclude an entropic stabilisation, the entropy due to a stacking disorder will be of comparable importance than the configurational entropy of the layers.
In a simple structure model, the decagonal structure was described by a stacking of two dimensional tilings, wich are correlated by the introduction of stacking fault energies. The influence of these stacking fault energies to the order/disorder in the layers was investigated and first results will be presented.
Numerical experiments have been performed on the propagation of mode I cracks in a three-dimensional icosahedral model quasicrystal. In particular, the dependence on the plane structure and the influence of clusters have been investigated. For this purpose crack propagation in planes perpendicular to five-, two- and pseudo-twofold axes was studied. The samples are endowed with an atomically sharp crack and subsequently loaded by linear scaling of the displacement field. The response of the system is monitored by molecular dynamics simulations.
Brittle fracture without any crack tip plasticity is observed. The fracture surfaces turned out to be rough on the scale of the clusters. These are not strictly circumvented, but to some extent cut by the dynamic crack. However, compared to the flat seed cracks the clusters are intersected less frequently. Thus the roughness of the crack surfaces can be assigned to the clusters, whereas constant average heights of the fracture surfaces reflect the plane structure of the quasicrystal. Furthermore a distinct anisotropy with respect to the in-plane propagation direction is found. For example, in planes of fivefold symmetry, steps are produced by cracks moving along the pseudo-twofold direction, but not along the twofold direction.
The atomic dynamics and diffusion in decagonal Al-Ni-Co and Al-Cu-Co quasicrystals is studied by molecular dynamics simulations using realistic pair potentials derived from first principles by Moriarty and Widom. It turns out that the structure models of Mihalkovic, Cockayne and Abe, used in the simulations, are very stable up to the melting temperatures, which are at about 1200 K. While the transition metal matrix remains completely stable up to the melting temperature, the aluminium atoms become very mobile above 800 K. Despite this mobility, the overall quasicrystal structure is not destroyed during the simulations.
Close to the melting temperature, the mobility of aluminium atoms becomes so high that long range diffusion can be observed. The diffusion constants have been measured as a function of temperature, from which the activation enthalpies and the pre-exponential factors of the diffusion processes are determined.