Seminars (Colloquium)
Schedule:
Friday, 03.05.2024, 16:00 c.t., D5-153: Jürgen Schnack, Bielefeld
The Unreasonable Effectiveness of the Finite Temperature Lanczos Method
Friday, 24.05.2024, 16:00 c.t., X-E0-200: Stefan Rotter, Freiburg
tba
Friday, 12.07.2024, 16:00 c.t., X-E0-200: Annika Hoyer, Bielefeld
tba
Friday, 19.07.2024, 16:00 c.t., H9: Johannes Schmidt-Hieber, Twente
Statistical learning in biological neural networks
Compared to artificial neural networks (ANNs), the brain learns faster, generalizes better to
new situations and consumes much less energy. ANNs are motivated by the functioning of the
brain but differ in several crucial aspects. For instance, ANNs are deterministic while
biological neural networks (BNNs) are stochastic. Moreover, it is biologically implausible
that the learning of the brain is based on gradient descent. In this talk we look at biological
neural networks as a statistical method for supervised learning. We relate the local updating
rule of the connection parameters in BNNs to a zero-order optimization method and derive some
first statistical risk bounds.
Winter Semester 2023/2024
Friday, 26.01.2024, 16:00 c.t., V2-213: Roland Langrock (Bielefeld)
Periodic variation in hidden Markov models
Abstract:
The class of hidden Markov models (HMMs) is a popular tool for mo-
delling time series driven by underlying states. HMMs can be used
for example to relate animal movement processes to underlying beha-
vioural modes, to infer the disease state of a patient from biomarkers,
or to predict extreme share returns as a function of the underlying ner-
vousness of the financial market. After a general introduction to this
versatile class of time series models, I will focus on one particular ex-
tension of HMMs, namely model formulations that attempt to capture
periodic variation in the state-switching dynamics (e.g. daily variation
in animal behaviour, or seasonality in economic markets). Such peri-
odic variation is commonly modelled using trigonometric functions, but
can alternatively and more flexibly be incorporated using cyclic splines.
I will showcase these modelling approaches in case studies, in which
I will also illustrate a positive consequence of such periodic modelling,
namely that for periodic HMMs the distributions of the dwell times in
the different system states can deviate substantially from a geometric
distribution as it would be implied by a homogeneous HMM.
Friday, 12.01.2024, 16:00 c.t., V2-213: Vitali Wachtel (Bielefeld)
Probabilistic approach to risk processes with level-dependent premium rate
Abstract:
In this talk I shall discuss classical risk processes and risk processes
with level dependent premium rate. I shall present a purely probabilistic
approach to processes with level-dependent rate, which allows one to
obtain upper and lower bounds for ruin probabilities.
Friday, 08.12.2023, 16:00 c.t., V2-213: Carolin Herrmann (Berlin)
Statistically proven? - the role of a valid sample size calculation in clinical trials
Abstract:
Randomized clinical trials are the preferred study design for answering medical research questions in
an evidence-based way. Apart from a research idea, different aspects have to be decided on when planning
a clinical trial, e.g. the treatments to compare with, the endpoints and the sample size.
Clinical trials can only be deemed successful if they come along with a valid sample size planning.
Sample sizes should be large enough to detect an existing relevant effect with a sufficient probability.
At the same time, they are supposed to be as small as possible to keep possible study related risks low
and to not postpone a potential market approval unnecessarily.
After a short introduction to clinical trials, we consider the basic concept of sample size planning as
well as more advanced statistical methods for updating sample sizes during ongoing trials.
Tuesday, 28.11.2023, 16:00 c.t., X-E0-200: Alexander Schönhuth (Bielefeld)
Diffusion Models: A Tutorial
Abstract:
Diffusion models have been one of the fundamental building
blocks of generative deep learning techniques such as "text-to-image"
models. In essence, diffusion models reflect a novel, neural network
guided sampling strategy. They apply for heavily complex probability
distributions. They are based on the general idea that only artificial
intelligence techniques can lead one the way from random number
generation to, for example, random images showing beaches with palm
trees. I will discuss the mathematical and computational foundations of
these models. I will also point out why such models may have the
potential in attempts to "generate random life".
Friday, 10.11.2023, 16:00 c.t., D2-136: Arndt von Haeseler (Vienna)
Single-cell RNA sequencing and phylogenetic inference
Abstract:
In the talk we will merge the emerging field of scRNA sequencing data with the established field
of phylogenomics. We will show that a simple transformation of the complex and high-dimensional scRNA
data and the subsequent phylogenetic analysis leads to surprisingly clear visualisations and can thus
provide the basis for new biological insights. The talk will be rounded off with some illustrative
examples.
This is joint work with Christiane Elgert and Julia Naas.
Summer Semester 2023
Monday, 17.07.2023, 16:00 c.t., D2-136: Mike Steel (Christchurch, New Zealand)
Phylogenetic theory in conservation biology
Abstract:
The current rapid extinction of species leads not only to their loss, but also to the disappearance
of the pendant and interior branches in the underlying evolutionary tree, along with the unique features
(e.g. traits) that have evolved along these branches. In this talk, I describe some recent and new
results for quantifying different measures of phylogenetic diversity and for predicting its loss under
simple extinction models.
Friday, 14.07.2023, 16:00 c.t., D2-136: Kai-Uwe Bux, Bielefeld
The Greek way of saying "let epsilon be greater than zero"
Abstract:
Proving equality of areas, lengths or angles was an important aspect of ancient
geometrical thought (that's what the word "metric" indicates). For polygonal areas,
the standard method is "cut and rearrange". This method does not apply in all cases
for volumes or areas of curved shapes like circles.
Archimedes in particular was very fond of integrating curved areas and volumes.
We now know that limits are unavoidable in this case. So, our colleagues from antiquity
(and among them Archimedes) did run into this problem; and they solved it very much in
the same way that Cauchy and Weierstrass did. There is but one difference: the Greeks
did neither have the concept of a real number nor did they think about functions.
I shall outline the way in which ancient mathematicians dealt with
limit arguments in a purely geometric fashion where one only deals
with quantities and ratios without identifying those with numbers.
Friday, 21.04.2023, 16:00 c.t., D2-136: Martin Wahl (Bielefeld University)
Principal component analysis in infinite dimensions
Abstract:
In high-dimensional settings, principal component analysis (PCA) reveals some unexpected phenomena,
ranging from eigenvector inconsistency to eigenvalue (upward) bias. While such high-dimensional
phenomena are now well understood in the spiked covariance model, the goal of this talk is to present
some extensions for the case of PCA in infinite dimensions. As applications, I will discuss the
prediction error of principal component regression (PCR) in the overparametrized regime, as well as
nonlinear dimensionality reduction methods such as Laplacian eigenmaps and diffusion maps.
Winter Semester 2022/2023
Friday, 27.01.2023, 16:00 c.t., online: Susanne Ditlevsen (Copenhagen)
Time scales in early warnings: how to predict the time of tipping?
Zoom Room,
Meeting ID: 674 2419 1845,
Passcode: 524697
Abstract:
In recent years there has been an increasing awareness of the risks of collapse or tipping points
in a wide variety of complex systems, ranging from human medical conditions, pandemics, ecosystems
to climate, finance and society. Though these are governed by very different dynamics, they are
characterized by variations on multiple spatial and temporal scales. This leads to incomplete
understanding or uncertainty in modelling of the dynamics. Even in systems where governing equations
are known, such as the atmospheric flow, predictability is limited by the chaotic nature of the
systems and by the limited resolution in observations and computer simulations. In order to progress
in analyzing these complex systems, assuming unresolved scales and chaotic dynamics beyond the
horizon of prediction as being stochastic has proven itself efficient and successful.
When complex systems undergo critical transitions by changing a control parameter through a critical
value, a structural change in the dynamics happens, the previously statistically stable state ceases
to exist and the system moves to a different statistcally stable state. In order to establish under
which conditions an early warning for tipping can be given, we consider a simple stochastic model,
which can be considered a generic representative of many complex two state systems. We show how this
provides a robust statistical method for predicting the time of tipping. The medthod is used to give
a warning of a forthcoming collapse of the Atlantic meridional overturning circulation.
References:
Ditlevsen, P.D., Ditlevsen, S. (2022). Warning of a forthcoming collapse of the Atlantic meridional
overturning circulation. Research Square https://arxiv.org/abs/2006.01289
Friday, 20.01.2023, 16:00 c.t., H11: Boris Hemkemeier (Commerzbank Frankfurt)
Twenty years of cybercrime and what we can do about it
In the early 2000s, phishing spilled over from the USA to Europe. In the meantime,
operating systems have become more secure, customers have become more aware and the
technical procedures in online banking are almost impossible to overcome in practice.
Nevertheless, cybercrime is a growth industry, because the attacks have shifted from
technology to trickery. Phishing, technician support and WhatsApp fraud, grandson trick 2.0.
But also CFO fraud and even ransomware thrive on storytelling alone. We discuss, which
countermeasures are effective beyond secure technology and what challenges lie in
modeling cyber risks.
Friday, 16.12.2022, 16:00 c.t., X-E0-203: Marie Doumic (Paris)
What triggers bacterial division? Mathematical modelling and inference for bacterial population dynamics
Abstract:
What triggers the bacterial division? To answer this question, several types of mathematical models
have been built, studied, and more recently compared to experimental data on growing and dividing
bacterial population. This is the field of structured population equations and stochastic processes,
which knows a long-lasting interest for more than sixty years, leading to much progress in their
mathematical understanding. They have been developed to describe a population dynamics in terms of
well-chosen traits, assumed to characterize well the individual behaviour. More recently, thanks to
the huge progress in experimental measurements, the question of estimating the parameters from
population measurements also attracts a growing interest, since it finally allows to compare model
and data, and thus to validate - or invalidate - the "structuring" character of the variable.
However, the so-called structuring variable may be quite abstract ("maturity", "satiety"...), and/or
not directly measurable, whereas the quantities effectively measured may be linked to the structuring
one in an unknown or intricate manner. We can thus formulate a general question: is it possible to
estimate the dependence of a population on a given variable, which is not experimentally measurable,
by taking advantage of the measurement of the dependence of the population on another - experimentally
quantified - variable?
In this talk, we give first hints to answer this question, addressing it first in a specific setting,
namely the growth and division of bacteria, and focus on a specific recently introduced model, the
so-called "increment of size"-structured equation, where the division depends on the increment of size
between birth and division.
Summer Semester 2022
Tuesday, 12.04.2022, 16:00 c.t., online and in Y-1-201:
Thomas Hillen (University of Alberta)
Non-local Models for Cellular Adhesion
Zoom Room
Meeting ID: 945 6235 5050,
Passcode: 246256
Abstract:
Cellular adhesion is one of the most important interaction forces between
cells and other tissue components. In 2006, Armstrong, Painter and Sherratt
introduced a non-local PDE model for cellular adhesion, which was able to
describe known experimental results on cell sorting and cancer growth.
Since then, this model has been the focus of applications and analysis. The
analysis becomes challenging through non-local cell-cell interaction and
interactions with boundaries. In this talk I will present theoretical
results of the adhesion model, such as a random walk derivation,
biologically realistic boundary conditions, pattern formation and results
on local and global existence of solutions.
(joint work with A. Buttenschoen, K. Painter, A. Gerisch, M. Winkler).
Winter Semester 2021/2022
Friday, 26.11.2021, 16:00 c.t., Online and in V2-210/216,
Peter Bühlmann (ETH Zurich)
Statistical Learning: Causal-oriented and Robust
Zoom Room,
Meeting ID: 930 2011 6784,
Passcode: 462251
Abstract:
Reliable, robust and interpretable machine learning is a big emerging theme in data science and artificial intelligence, complementing the development
of pure black box prediction algorithms. Looking through the lens of statistical causality and exploiting a probabilistic invariance property
opens up new paths and opportunities for enhanced interpretation, robustness and external validity, with wide-ranging prospects for various
applications.
Friday, 19.11.2021, 16:00 c.t., Online: Claudia Neuhauser (University of Houston)
Mathematical Models of Host-Symbiont Interactions
Zoom Room,
Meeting ID: 973 1183 7014,
Passcode: 367914
Abstract:
Host-symbiont interactions are ubiquitous in nature. They can involve pathogens and mutualists and have different levels of specificity. We
will first introduce some general models before applying the modeling framework to virotherapy of cancer. Virotherapy of cancer relies on
engineered viruses that selectively attack and kill cancer cells but leave healthy cells unaffected. The success of this therapy relies on
the successful establishment of an infection that results in the death of cancer cells. We used spatially explicit, stochastic models of
multi-species interactions to map out under what conditions the symbiont (virus) effectively eliminates the host (cancer cells). I will present
rigorous results and conjectures based on simulations. I will report on an experimental system (in vitro and in vivo) that was developed by Dr.
David Dingli (Mayo Clinic) and uses this mathematical framework to predict the effectiveness of virotherapy in cancer.
Summer Semester 2021
Friday, 25.06.2021, 16:00 c.t., Online: Arndt von Haeseler (Wien University)
Evolution of taboo free sequences
Zoom Room,
Meeting ID: 961 4237 2382,
Passcode: 970387
Abstract:
Models of sequence evolution typically assume that all DNA-sequences are possible. However, restriction enzymes that cut DNA at specific recognition sites provide an example where carrying a recognition site can be evolutionary disadvantageous.
Motivated by this observation, we studied the set of DNA sequences with \textbf{taboos}, that is, with prohibited $k$-mers. The taboo-set is referred to as $\mathbb{T}$ and any allowed DNA as a taboo-free DNA. We consider the so-called Hamming graph $\Gamma_n(\mathbb{T})$, with taboo-free DNA of length $n$ as vertex set and whose edges connect two taboo-free DNA if their Hamming distance equals one. Any (random) walk on this graph describes the evolution of a DNA sequence that avoids taboos. We describe the construction of the vertex set of $\Gamma_n(\mathbb{T})$. Then we state conditions under which $\Gamma_n(\mathbb{T})$ and its suffix subgraphs are connected. Moreover, we provide an algorithm that determines if all these graphs are connected for an arbitrary $\mathbb{T}$. Finally, we give some illustrative examples how taboo sequence influence distance estimation. Moreover we discuss more general aspects of taboo sequences, when discussing evolution.
This is joint work with Cassius Manuel, Dominic Földvari, Stephan Pfannerer (lexicographical order by the first name)
Ref: C. Manuel, A von Haeseler (2020) J. Math. Biology 81:1029-1057
Winter Semester 2020/2021
Friday, 19.03.2021, 16:00 c.t., Online: Alexander Schoenhuth (Universität Bielefeld)
Capsule Networks - a brief tutorial and applications in biology
Zoom Room,
Meeting ID: 926 4815 6073,
Passcode: 042902
Abstract:
I will provide a brief tutorial about capsule networks (CAPNs), and
explain in particular what distinguishes them from convolutional neural
networks (CNNs). Although suggested as a useful concept already earlier,
CAPNs enjoyed their first successful application in 2017, eventually.
The motivation that underlies the design of CAPNs is to overcome
technical challenges that affected CNNs, in particular when dealing with
distorted or overlapping images. Key to success is to have neurons, the
fundamental units of neural networks, being modeled as vectors (in
CAPNs) instead of just scalars (as in CNNs). One major advantage of
CAPNs was found to be the interpretability of the capsules, as
fundamental building blocks. Time allowing, I will present two
applications in biology, where interpretability of predictions is a
crucial concern.
Friday, 19.02.2021, 16:00 c.t., Online: Adam Mielke (Universität Bielefeld)
Territorial behaviour of birds of prey versus random matrix spacing distributions
Zoom Room,
Meeting ID: 954 2522 3899,
Passcode: 367638
Abstract:
We investigate the territorial behaviour of buzzards in the Teutoburger Forest by performing a large-scale analysis of nest positions gathered over the last 20 years.
We use comparison of the nearest and next-to-nearest neighbour distributions to those of a Coulomb gas as a measure of the territorial behaviour by quantifying the strength and range of repulsion between the points.
A one-parameter fit is made to a moving time average, using the charge of the particles as the fitting parameter. It reveals a significant increase in repulsion over the observed period of time that coincides with an increase in population.
This effect is seen for both nearest and next-to-nearest neighbours, though the effect is smaller for the next-to-nearest neighbour, which indicates short-range interaction.
Our results correlate well with concepts of population ecology.
This is joint work with Gernot Akemann, Michael Baake, Nayden Chakarov, Oliver Krüger, Meinolf Ottensmann, and Rebecca Werdehausen
Friday, 12.02.2021, 16:00 c.t., Online: David Kikuchi (Universität Bielefeld)
Signals, true and false: evolutionary and ecological consequences of decision-making under risk
Zoom Room,
Meeting ID: 920 8144 5044, Passcode: 036718
Abstract:
Exact analytical solutions for population genetic models are
rarely possible because of the complex interplay between recombination
and other processes. Simulation is therefore a fundamental tool in
population genetics, as it allows us to explore the models that we are
interested in, evaluate analytical approximations, and to fit parameters
for these models to data. We show how a recently introduced data
structure, the "succinct tree sequence", allows us to simulate these
ancestral processes exactly for millions of samples, a speed increase of
several orders of magnitude over the previous state-of-the-art.
Friday, 20.11.2020, 16:00 c.t., Online: Jerome Kelleher (Big Data Institute, Oxford University)
Simulating ancestral processes for large samples
Zoom Room,
Meeting ID: 998 4232 9998, Passcode: 640513
Abstract:
Exact analytical solutions for population genetic models are
rarely possible because of the complex interplay between recombination
and other processes. Simulation is therefore a fundamental tool in
population genetics, as it allows us to explore the models that we are
interested in, evaluate analytical approximations, and to fit parameters
for these models to data. We show how a recently introduced data
structure, the "succinct tree sequence", allows us to simulate these
ancestral processes exactly for millions of samples, a speed increase of
several orders of magnitude over the previous state-of-the-art.
Friday, 13.11.2020, 16:00 c.t.: Ulrike Schlägel (Universität Potsdam)
Movement-mediated community assembly and coexistence
Zoom Room,
Meeting ID: 973 7063 5015, Passcode: 184489
Abstract:
Biodiversity trends due to anthropogenic environmental change are varied. While we experience an overall loss of species, individual communities and metacommunities may increase or decrease in diversity, depending on spatial and environmental factors as well as the intricacies of species' interactions within their environments. Many of the processes that shape community composition and allow species coexistence are mediated by organismal movements. Yet, bridging from movement processes at the small scale of individuals to species interactions at the community scale is challenging. In this talk, I will present some of my work on integrating movement ecology and biodiversity research by means of synthesis as well as conceptual and statistical developments.
Summer Semester 2020
Friday, 08.05.2020, 16:00 c.t., Online: Lorenzo Sadun (University of Texas, USA)
The problem of latency in estimating the Covid-19 replication number R0.
Abstract:
Figuring out how to restart the world's economy without a
resurgence of disease depends on understanding how contagious Covid-19
really is. However, estimates of the basic replication number $R_0$ vary
greatly, with well-respected groups publishing estimates whose 95%
confidence intervals don't even overlap. In this talk I'll go over the
basic
SIR and SEIR models of disease spread and present several different ways to
treat the latency period between being exposed and becoming infectious.
Simple SEIR models are unstable; working with a fixed set of data, small
changes to the model can result in large changes to the estimated value of
$R_0$. More realistic models are more complicated and are even less stable.
The upshot is that we know much less about $R_0$ than is generally
believed,
and the error bars on the high side are particularly large. Containing the
outbreak for an extended period may be a lot harder than our leaders
think.
Winter Semester 2019/2020
Wednesday, 19.02.2020, 10:00 s.t., CITEC 1.204: Marc Alexa (TU Berlin)
Representing Frames as Möbius Transformations — Complementing Quaternions with a Measure for Deformations
Abstract:
Let us say that a frame is given by three ‘sticks’ (of equal lengths) meeting in one common point. We are interested in representing the orientation and the ‘shape’ of the frame. Orientation is the rotation relative to a reference frame; and ‘shape’ is the deformation relative to a reference frame. It turns out that any frame can be turned into any other frame by a Möbius transformation. This viewpoint reveals that rotations are points on a 3-sphere, the so-called unit quaternions. Unit quaternions are well-known and quite useful as a representation for rotations in space — they are continuous in the variables, minimal in the sense that at least four coordinates are necessary for a continuous representation, and they come with a natural metric that allows us to measure the ‘amount’ of rotation, i.e. the angle. The viewpoint of Möbius transformations also reveals, and this is the new aspect of this work, that deformations are points on a hyperboloid. So ‘shape’ can be described as a point in hyperbolic space. This is a representation that, just like unit quaternions, is continuous, small, and comes with a natural metric that allows measuring the amount of deformation.
Friday, 08.11.2019, 16ct, V3-204: Jochen Röndigs (Bielefeld)
Following manifolds in equivariant evolution equations - a generalisation of the freezing method to infinite-dimensional symmetry
Abstract:
Equivariant evolution equations possess a symmetry described by a Lie group that acts on the phase space. The freezing method separates the dynamics of such an equation into dynamics within the symmetry group and within the phase space. The method has successfully been used to 'freeze' wave patterns in PDEs. However so far only finite-dimensional Lie groups have been considered.
This talk presents a generalisaton of the freezing method to infinite-dimensional symmetry. To do so manifolds are studied and the symmetry group employed is the group of diffeomorphisms. The application of the freezing method is developed for this case introducing additional free variables which provide extra degrees of freedom within the group. Special attention is paid to the control of these variables as they determine the dynamics within the group which carries out the true feature of the freezing method. New control techniques had to be designed for the infinite-dimensional setting since the free variables satisfy a differential equation themselves. A numerical approach is described as well to illustrate the results by following close curves and tori in dynamical systems over time. Especially invariant sets, level curves and attractors, were considered to demonstrate various splittings of dynamics.
Summer Semester 2019
Tuesday, 11.06.2019, 14ct, U10-146: Mike Steel (Christchurch, New Zealand)
Birth-death models in phylogenetics: symmetries, shapes, and the loss of biodiversity
Abstract:
The role of birth-death processes in modelling speciation and extinction
in macro-evolution has a long history, with a classic paper by Yule in
the 1920s. In this talk, I describe how such models can predict the
‘shape’ of evolutionary trees, as well as the expected loss of
phylogenetic diversity under rapid extinction at the present.I also
describe some recent work revealing certain symmetries in these
processes, which has implications for the inference of speciation and
extinction rates from phylogenies.
Friday, 24.05.2019, 16ct, V3-204: Elisabeth Georgii (München)
Data-driven plant science: from multi-omics analysis to phenotype modeling
Abstract:
High-throughput omics technologies provide comprehensive measurements of tens of
thousands of molecular features at different levels of cellular organization.
Integrating such high-dimensional and heterogeneous data to facilitate discovery
of biological relationships poses various computational challenges, starting from
appropriate data management and automated analysis workflows up to advanced machine
learning, data mining and visualization techniques. This talk highlights examples
of data-driven hypothesis generation regarding biological mechanisms of combined
drought and heat stress responses in plants, which are increasingly important
under predicted climate change scenarios. In particular, both correlated and
contrasting regulation patterns between the transcriptome and the metabolome are
put into biological context. Even after stress relief and during extended recovery
periods, plants maintain a molecular memory that increases their tolerance to
subsequent stress events. Our data suggest that this memory differs with stress
frequency or intensity, exists across tissues, involves specific genes and is
consistent with phenotypic observations. Finally, recent developments in plant
phenotyping and approaches toward integrative phenotype modeling are presented.
Friday, 10.05.2019, 16ct, V3-204: Michael Baake (Bielefeld)
The Markov embedding problem revisited - from an algebraic perspective
Abstract:
The Markov embedding problem, namely whether a given
Markov matrix can occur within a continuous time Markov
semigroup, is still unsolved even for 4x4 matrices.
It became quite famous in the 1960s through an influential
paper by Sir John Kingman and led to some interesting
equivalent reformulations, but defied a practically
effective solution already for 3x3 matrices for a long
time, and still does beyond. In this contribution, the
problem will be reviewed and some extensions will be
presented, which were triggered by the recent need in
phylogeny that has put the problem again on the table.
Winter Semester 2018/2019
Friday, 11.01.2019, 16ct, V3-204: Christiane Fuchs (Bielefeld University)
Stochastic Modelling and Inference of Cellular Processes
Abstract:
The molecular biology of life seems inaccessibly complex, and gene expression
is an essential part of it. It is subject to random variation and not exactly
predictable. Still, mathematical models and statistical inference pave the
way towards the identification of underlying gene regulatory processes. In
contrast to deterministic models, stochastic processes capture the randomness
of natural phenomena and result in more reliable predictions of cellular
dynamics. Stochastic models and their parameter estimation have to take into
account the nature of molecular-biological data, including experimental
techniques and measurement error.
This talk presents according modelling and estimation techniques and their
applications: the derivation of mRNA contents in single cells; the
identification of differently regulated cells from heterogeneous populations
using mixed models; and parameter estimation for stochastic differential
equations to understand translation kinetics after mRNA transfection.
Friday, 19.10.2018, 16ct, V3-204: Philip Gerrish, Atlanta/Bielefeld
Is there sex on other planets?
Abstract:
We ask the question: if an alien system of self-replicating
entities were discovered, should we expect sex and/or recombination to
be features of this system? Put differently, is there something about
mutation and natural selection that inherently promotes the evolution of
sex and recombination? Current theory finds many special circumstances
in which sex and recombination might be expected to evolve, but this
“patchwork of special cases” (with many holes) does not seem to fit the
observations: in nature, sex and recombination are everywhere — spanning
all environments and all levels of organismal size and complexity.
Increasingly, even species traditionally thought to be asexual have been
caught “having sex on the sly”. The observations, therefore, seem to
call for an encompassing feature common to living things in general that
promotes the evolution of sex and recombination. And we think we may
have a candidate! We think this general feature might be none other than
natural selection itself. I will show you what we’re thinking and how it
works, will go through the case of structured populations which has a
nice intuitive “visual proof” as well as a presentable “simplest case”
proof, and will show you how far we’ve gotten with the full problem,
with hopes for some nice feedback.
This is joint work with Ben Sprung (Philadelphia), Julien Chevallier
(Grenoble), and Bernard Ycart (Grenoble).
Summer Semester 2018
Wednesday, 30.05.2018, 16ct, U10-146: Carsten Wiuf (Copenhagen)
Stochastic modelling and analysis of DNA sequence data from Follicular Lymphoma
Abstract:
An cancer evolution model is proposed at the level of the
individual cells, similar to other models that are used in population
genetics to model the evolution of populations. The focus is on a
particular form of cancer, called Follicular Lymphoma. A population of
tumor cells initiates from a single cell harboring a
t(14,18)-translocation which is considered a precursor step to
Follicular Lymphoma. From there on the tumor evolves by accumulation of
other driver and passenger mutations.
A mathematical model is derived akin to coalescent models and various
properties of the model are discussed in relation to statistical
inference from DNA sequence data. DNA sequence data from primary and
relapse tumors from (approx) 15 individuals are subsequently analyzed
using the model, and parameters and the time of origin of the tumors are
estimated.
Friday, 15.06.2018, 16ct, U10-146: Mike Steel (Christchurch, New Zealand)
The combinatorics of ‘capturing’ a phylogenetic tree from discrete
characters or distances
Abstract:
We consider two versions of the following question: What is
the smallest amount of ‘data’ required to uniquely determine a
phylogenetic (evolutionary) tree?In the first version, the ‘data’
consists of discrete characteristics observed at the leaves of a tree,
and these characteristics are assumed to have evolved from an unknown
ancestral state without homoplasy. For the second version, the data
consists of leaf-to-leaf distances between certain pairs of leaves in
the tree. Both questions give rise to interesting combinatorial
subtleties, and lead to two recent mathematical results.
Friday, 27.04.2018, 16ct, V3-204: Jens Stoye (Bielefeld University)
On Indexing for Jumbled Pattern Matching
Abstract:
Jumbled pattern matching is a variant of string matching where the order
of characters in the matched region is ignored. It has applications in
various areas of bioinformatics and beyond. Like in ordinary string
matching, indexing allows to speed-up the search of multiple patterns in
the same text.
Recently, the problem of indexing binary strings for jumbled pattern
matching has received quite some attention. While it seems unlikely to
develop faster algorithms in terms of input size, we can still make
progress on the problem by considering other natural parameters. One
such parameter is the number of runs of 1s in the input, i.e. the length
of the run length encoding (RLE) of the input string.
We present a new and very simple algorithm matching the best known
running times. This algorithm can be extended, either so that the index
returns the position of a match (if there is one), or so that the
algorithm uses only \$n\$ bits of space instead of \$n\$ words.
To better understand the behaviour of the latter variant, we also study
some combinatorial problems arising from comparing the RLE of the input
string to the RLE of the binary output string. Some of these problems
are still open, and any idea from the audience will be highly appreciated.
This is joint work with Luis Kowada, Luís Felipe Cunha, Roland Wittler,
Travis Gagie, Szymon Grabowski and maybe others.
Wednesday, 02.05.2018, 16ct, T2-204: Scott Balchin (Warwick/Sheffield)
Introduction to topological methods in data analysis
Abstract:
Persistent homology is a method of analyzing features of point-cloud
style data which persist across multiple scales. This exciting new
method of data analysis is being found increasingly applicable in the
study of 'big data'. For example, applications are being explored in the
study of directed networks, image compression, and the analysis of
recombination, reassortment and horizontal gene transfer in
phylogenetics. As the method is purely topological, it works on data of
any dimension, and is actually coordinate free. The goal of this talk is
to describe the steps required to compute the PH of some data-set,
including the algorithms involved, and to discuss how one should
interpret the results. I will then go on to explain the limitations of
the method, as well as variations such as applications to different data
types, and multi-dimensional persistence.
Winter Semester 2017/2018
Friday, 12.01.2018, 16ct, V3-204: Roland Langrock (Bielefeld University)
Spline-based nonparametric inference in general state-switching models
Abstract:
Hidden Markov models (HMMs) and their various extensions have been
successfully applied in various disciplines, including biology, speech
recognition, economics/finance, climatology, psychology and medicine.
They combine immense flexibility with relative mathematical simplicity
and computational tractability, and as a consequence have become
increasingly popular as general-purpose models for time series data. In
this talk, I will demonstrate how the HMM machinery can be combined with
penalised splines to allow for flexible nonparametric inference in
HMM-type classes of models. The focus of the presentation will lie on
practical aspects of nonparametric modelling in these frameworks, with
the methods being illustrated in ecological and economic real data examples.
Friday, 27.10.2017, 16ct, V3-204: Meike Wittmann (Bielefeld University)
Fluctuating balancing selection and its effects on neutral genetic diversity
Abstract:
For organisms with several generations per year, seasonally fluctuating
selection can be a powerful mechanism to maintain genetic polymorphism.
For example, an allele favored during summer may stably coexist with an
allele favored during winter, a form of balancing selection. Despite
intense debate over decades, it is still unclear how much of the
variation observed in the genomes of natural populations is due to
balancing selection. In recent years, evolutionary biologists have
started scanning genomes for genetic footprints of balancing selection
(e.g. regions of increased diversity). However, these scans have
generally assumed the simplest form of balancing selection where alleles
are maintained at constant frequencies over time. There is currently
insufficient theory to tell us what genetic footprint to expect under
seasonally fluctuating selection, and how to distinguish it from
neutrality but also from other forms of balancing selection. In this
talk I will present results from coalescent models and stochastic
simulations to characterize the impact of fluctuating balancing
selection on neutral genetic diversity at various scales: at closely
linked sites, at the scale of the chromosome, and at the genomic scale.
Summer Semester 2017
Tuesday, 13.06.2017, 16ct, V3-201: Mike Steel (University of Canterbury, New Zealand)
Phylogenetic questions inspired by the theorems of Arrow and Dilworth
Abstract:
Biologists frequently need to reconcile conflicting estimates
of the evolutionary relationships between species by taking a
‘consensus’ of a set of phylogenetic trees. This is because different
data and/or different methods can produce different trees. If we think
of each tree as providing a ‘vote’ for the unknown true phylogeny, then
we can view consensus methods as a type of voting procedure. Kenneth
Arrow’s celebrated ‘impossibility theorem’ (1950) shows that no voting
procedure can simultaneously satisfy seemingly innocent and desirable
properties. We adopt a similar axiomatic approach to consensus and asks
what desirable properties can be jointly achieved.
In the second part of the talk, we consider phylogenetic networks (which
are more general than trees as they allow for reticulate evolution).The
question ‘when is a phylogenetic network merely a tree with additional
links between its edges?’ is relevant to biology and interesting
mathematically. Such ‘tree-based’ networks can be efficiently
characterized.We describe these along with new characterization results
related to Dilworth’s theorem for posets (1950), and matching theory on
bipartite graphs.In this way, one can obtain fast algorithms for
determining when a network is tree-based and, if not, to calculate how
‘close’ to tree-based it is.
Monday, 10.04.2017, 16 ct, U10-146: Reinhard Bürger (Vienna)
Two-locus clines on the real line
Abstract:
A population-genetic migration-selection model will be investigated which is
continuous in space and time. The model assumes that two diallelic, recombining
loci are under selection caused by an abrupt environmental change. The habitat
is linear and unbounded, and dispersal occurs by diffusion. Selection is modeled
by step functions such that in one region one allele at each locus is advantageous
and in the other deleterious. Environmentally independent, intermediate dominance
at both loci is admitted. The nonconstant stationary solutions of the resulting
system of PDEs are called clines. First, an explicit expression for the single-locus
cline with dominance is derived, thus generalizing classical results by Haldane
and others. Interestingly, the slope of the cline in the center turns out to be
independent of dominance. Second, under the assumption of strong recombination,
the first-order approximation of the allele-frequency cline at each of the loci
is derived, as is the linkage disequilibrium. Therefore, we obtain the
quasi-linkage-equilibrium approximation of the two-locus cline. Its asymptotic
properties are characterized explicitly. The consequences of dominance and linkage
for the shape of the two-locus cline are explored for arbitrary recombination rates.
Analogous models on a bounded habitat will be discussed briefly.
Winter Semester 2016/2017
Friday, 18.11.2016, 16 ct, V3-201: Bernd Sturmfels (Berkeley / Leipzig)
Does Antibiotic Resistance Evolve in Hospitals?
Abstract:
Nosocomial outbreaks of bacteria are well-documented. Based on these
incidents, and the heavy usage of antibiotics, it has been assumed
that antibiotic resistance evolves in hospital environments. To test this
assumption, we studied resistance phenotypes of bacteria collected from
patient isolates at a community hospital. A graphical model analysis
shows no association between resistance and patient information other
than time of arrival. This allows us to focus on time course data.
We introduce a Hospital Transmission Model, based on negative binomial
delay. Our main contribution is a statistical hypothesis test called the
Nosocomial Evolution of Resistance Detector (NERD). It calculates the
significance of resistance trends occurring in a hospital. It can help
detect clonal outbreaks, and is available as an R-package. We applied
the NERD method to each of the 16 antibiotics in the study via 16
hypothesis test. For 13 of the antibiotics, we found that the hospital
environment had no significant effect upon the evolution of resistance;
the p-values obtained for the other three antibiotics indicate that
care should be taken in hospital practices with these antibiotics.
This is joint work with Anna Seigal, Portia Mira and Miriam Barlow.
Friday, 28.10.2016, 16 ct, V3-204: Andreas Richter (Bielefeld University)
Evolvability as a quality criterion for linear deformation representations in evolutionary design optimization
Abstract:
Industrial product design is characterized by increasing complexity due to the
high number of involved parameters, objectives, and boundary conditions, all
typically changing over time. Population-based evolutionary design optimization
targets to solve these kinds of application problems, offering efficient algorithms
striving for high-quality solutions. An important factor in the optimization setup
is the representation, which defines the encoding of the design and the mapping
from parameter space to design space. Being able to numerically quantify the quality
of different representation settings would strengthen the optimal choice of encoding.
Motivated by the biological concept of evolvability, we propose three criteria,
namely variability, regularity, and improvement potential, to evaluate linear
deformation representations for their use in shape optimization problems. The
first aspect characterizes the exploration potential of the design space, the
second measures the expected convergence speed, and the third determines the
expected improvement of the quality of a design. We propose and experimentally
analyze mathematical definitions for each of the three criteria. We demonstrate
the successful application of our model to two evolutionary optimization scenarios:
fitting of 1D height fields and fitting of 3D face scans, both based on RBF deformations.
Furthermore, we analyze the construction of optimal RBF deformation setups towards the
three quality criteria.
Summer Semester 2016
Monday (!) , 05.09.2016, 16 ct, V3-204 : Markus Nebel (Universität Bielefeld)
Analytic Combinatorics in Biology and Chemistry
Abstract:
At the latest with the computerization of many branches of their research discrete models became of increased importance to biologists and chemists.
With the application of those models various quantitative questions were posed, most of which could be answered by methods from analytic combinatorics.
Often, a special feature in this domain is the use of formal languages instead of directly applying the so-called symbolic method.
In this talk we will discuss some representative examples showing the elegance of the method together with some of its enhancements in the context of biology and chemistry.
Friday, 15.07.2016, 16 ct, V3-204: Martin Möhle (Universität Tübingen)
On hitting probabilities of some Markov chains arising in mathematical population genetics - oscillation versus convergence
Abstract:
We derive some properties of the Greenwood epidemic Galton--Watson branching model.
Formulas for the probability \$h(n,m)\$ that the associated Markov chain
\$X\$ hits state \$m\$ when started from state \$n\ge m\$ are obtained. For
\$m\ge 1\$ it follows that \$h(n,m)\$ slightly oscillates with varying \$n\$
and has infinitely many accumulation points. In particular, \$h(n,m)\$ does not
converge as \$n\to\infty\$. It is shown that there exists a Markov chain \$Y\$
which is Siegmund dual to \$X\$. The hitting probabilities of the dual chain \$Y\$
are investigated. The second part of the talk addresses similar questions for the
block counting process \$X\$ of the Bolthausen--Sznitman coalescent or more generally
of the \$\beta(2-\alpha,\alpha)\$-coalescent with parameter \$0<\alpha<2\$.
In this case the hitting probabilities \$h(n,m)\$ converge as the sample size \$n\$ tends
to infinity. Formulas for the asymptotic hitting probabilities \$h(m):=\lim_{n\to\infty}h(n,m)\$ are provided.
Freitag, 10.06.2016, 16 ct, V3-204: Barbara Hammer (Universität Bielefeld)
Prototype-based machine learning models - some advances and open problems
Abstract:
Prototype-based machine learning techniques offer efficient nearest neighbor-based models
for data classification: they represent a classification model in terms of typical prototypes
in the data space. Given a novel data point, its class is predicted as the class of its nearest
prototype. There do exist intuitive learning schemes, which can infer suitable prototypes
automatically from a given set of training data; further, the generalisation ability of
prototype-based classifiers can be accompanied by distribution-independent large-margin
generalization bounds, i.e. they provably display good generalization ability for novel
data points for i.i.d. training data.
These facts have contributed to an increasing popularity of such models in the domain of
biomedical data analysis or life-long learning, among others. Within the talk, we will address
two advances for prototype-based models, discussing the basic concepts as well as open problems:
(1) Metric learning - as distance based classifiers, prototype-based models fail whenever the used
distance is not suitable for the observed data. This can be cured by so-called metric learning
from data. We present basic concepts of metric learning and a recent application in the context
of transfer learning for the adjustment of a classifier due to misplaced sensors. We also discuss
the validity (and problems) of an interpretation of metric parameters as relevance terms.
(2) Reject option for classification - in the domain of safety-critical systems or life-long
learning, it becomes crucial to reject a classification for insecure regions of the classifier.
We discuss the question how to enhance a prototype-based classifier by optimum reject options
for the given training data.
Winter Semester 2015/2016
Friday, 18.03.2016, 16 ct, U10-146: Oliver Krüger (Universität Bielefeld)
Models in ethology
Abstract:
The talk will illustrate the role of mathematical models
in ethology in the context of population modelling, time
series analysis and optimality modelling. The talk will
demonstrate the importance of modelling for the evaluation
of data from current long-term studies. The population ecology of
birds of prey and the host-parasite coevolution of cuckoos
will serve as empirical examples.
Friday, 11.03.2016, 16 ct, V3-204 U10-146: Robert Giegerich (Universität Bielefeld)
Love over Gold? Mind over Matter? Pareto Optimization in Biosequence Analysis
Abstract:
Pareto Optimization is a technique to solve optimization problems under
multiple objectives,
while avoiding a mathematically questionable amalgamation of the objectives.
Pareto optimization returns all solutions from the search space that are
optimal in the sense
that their score cannot be improved in one objective without decreasing
it in some other objective.
Pareto optimzation has some convenient and interesting mathematical
properties - preservation of
Bellman's Principle, scale-freeness, and the existence of ghost solutions.
This makes it an attractive alternative to study biosequence analysis
problems that have previously
been tackled with pseudoscore approaches.
Pareto optimization is available at keystroke in the Bellman's GAP
dynamic programming system.
The talk will shed some light on how this is achieved, and what we can
do with it, using examples
from comparative RNA structure prediction and the intergation of
chemical probing data in RNA folding.
Freitag, 29.01.2016, 16ct, V3-204: Ulrike Schlägel (Universität Potsdam)
Models on the move: memory and temporal discretization in animal movement
Abstract:
Animal movement is an important ecological process. Many animals move to
meet their daily and lifetime needs related to maintenance, survival,
and reproduction. Movement of individuals scales up to population
patterns, affecting populations’ abundances and distributions as well as
community structures. Additionally, mobile animals provide important
services to ecosystems, transporting seeds, pollen or smaller organisms,
redistributing resources, or inducing disturbance regimes. During the
last decades, studies of animal movement have benefitted from major
advances in tracking technology that opened new dimensions for data
collection and analysis. In this talk, I present two lines of research
that address mathematical-statistical challenges of movement data
analysis. First, I present an approach to detect cognition-based
movement strategies in which animals consider their travel history for
movement decisions. Second, I discuss a fundamental problem that arises
when discrete-time movement data, e.g. GPS data, is analyzed by means of
discrete-time models such as random walks and their extensions.
Summer Semester 2015
Thursday, 25.06.2015, 14ct, U10-146: Mike Steel (University of Canterbury)
Combinatorial aspects of phylogenetic networks
Abstract:
Phylogenetic networks are directed graphs that display evolutionary relationships between
species, and which can accommodate reticulate processes (e.g. the formation of hybrid species,
or lateral gene transfer). In this talk, I will describe some recent combinatorial results
on phylogenetic networks, aimed at addressing three questions: When is a network merely
a tree with arcs between its branches? When can distances between taxa in a network appear
perfectly tree-like? Which networks remain the same when they are ‘unfolded’ and then
‘refolded’? I will also report briefly on a curious combinatorial property that applies to binary
planar networks, and which is algorithmically useful.
Friday, 12.06.2015, 16ct, U10-146: Stefan Rotter (Universität Freiburg)
Spike Train Correlations Induced by Anatomical Microstructure
Abstract:
Correlations in neuronal spike trains reflect the structure of the underlying network. Pairwise correlations are
caused, for instance, by direct synaptic interaction and by shared input. The contributions of more indirect,
multi-synaptic pathways, however, are also very important and can be described by accounting for the
connectivity motifs that arise in recurrent networks of arbitrary topology. Higher-order correlations can be dealt
with in an analogous way, and new results will be presented on how one can manage the associated
combinatorial problems. In recent work we were also able to demonstrate that the inverse problem of inferring
(directed) connectivity from (undirected) pairwise correlations can be approximately solved by a method based
on L1-optimization, provided that the networks are sparsely coupled but the level of sparsity is not too low.
Applications of such methods to neuronal populations that are observed through mass signals (e.g. ECoG or
MREG) are now pursued, using improved versions of the algorithm that exploit its specific algebraic structure.
Friday, 22.05.2015, 16ct, V3-204: Dr. Silvia Gruhn (University of Cologne)
Mathematical modeling of the neural control of insect locomotion
Abstract:
The mechanism underlying the generation of stepping has been the object
of intensive studies. Stepping involves the coordinated movement of
different leg joints and is, in the case of insects, produced by
antagonistic muscle pairs.\\
In the stick insect, the coordinated actions of three such antagonistic
muscle pairs produce leg movements and determine the stepping pattern of
the limb. The activity of the muscles is controlled by the nervous
system as a whole and more specifically by local neuronal networks for
each muscle pair. While many basic properties of these control
mechanisms have been uncovered, some important details of their
interactions in various physiological conditions have so far remained
unknown.\par
We have created a neuro-mechanical model of the coupled three joint
control system of the stick insect's middle leg to unravel details of
the neuronal and mechanical mechanisms driving a stepping single leg in
situations other than forward walking. The model can generate forward,
backward, or sideward stepping as well as searching movements. Using the
model, it is, because of it's detailed biological description, possible
to make detailed suggestions as to how rhythmic stepping might be
generated by the central pattern generators of the local neuronal
networks, how this activity might be transmitted to the corresponding
motoneurons, and how the latter might control the activity of the
related muscles. The entirety of these processes yields the coordinated
interaction between neuronal and mechanical parts of the system.
Moreover, based on experimental findings which state that only the
activity of the muscles which move the leg forward and backward is
reversed during backwards walking, we hypothesize and verify a mechanism
by which motoneuron activity is modified by a premotor network and
therefore suggest that this mechanism might serve as a basis for fast
adaptive behaviour, like switches between forward and backward stepping,
which occur, for example, during curve walking, and especially sharp
turning, of insects.
Tuesday, 19.05.2015, 16ct, U10-146: Susanne Schindler (University of Oxford)
The reproductive value in two-sex models of age- and size-structured populations
Abstract:
The reproductive value (RV) of an individual describes the fraction of a
future population that descended from it and is thus an important
fitness measure. Estimating the RV from two-sex models is challenging as
standard approaches to estimate the RV for one-sex models do not extend
to the two-sex case. Furthermore, the age and size structure of a
population renders a straightforward generalisation of Fisher's formula
for the RV impossible, because the size-trajectory of an individual has
to be taken into account. I demonstrate how to take individual
size-trajectories with their consequences for offspring production into
account and will present a way to calculate the RV in two-sex
age-and-size structured models.
Winter Semester 2014/2015
Fr 14.11.2014, 16 c.t.: Majid Salamat (Bielefeld),
Coupling from the past and perfect simulation
Fr 28.11.2014, 16 c.t.: Thorsten Hüls (Bielefeld),
Global bifurcations in a noninvertible model of asset pricing and a new approach for computing stable fibers
Fr 23.01.2015, 16 c.t.: Philipp Lampe (Bielefeld),
Computational methods in cluster theory
Fr 06.02.2015, 16 Uhr c.t.: Mario Botsch (Universität Bielefeld),
Flexible Simulation Techniques for Topological Changes of Elastic Bodies
Summer Semester 2014
Friday, 11.07.2014, 17ct, U10-146
Mike Steel, University of Canterbury
Autocatalytic sets and models of early life
Abstract:
A key step in the emergence of early life was the formation of a set of
reactions that is (i) self-sustaining (all reactions involve reactants
that are either produced by other reactions or are available in the
environment) and (ii) autocatalytic (each reaction is catalyzed by some
molecule produced by the system). Mathematical, algorithmic and
stochastic techniques can help define, analyse, classify and search for
these self-sustaining autocatalytic system in large chemical reaction
networks. It is also possible to compute the probability of such systems
forming in simple polymer models, as a function of the catalysis rate,
and to determine their size when they first arise. In this talk, I will
provide an overview of some of our earlier and more recent results in
this area. This is joint work with Wim Hordijk, Elchanan Mossel and others.
Friday, 11.07.2014, 16ct, U10-146
Arndt von Haeseler, University of Vienna
Modelling Coverage Patterns from High Throughput Sequencing
Technologies
Abstract:
High throughput sequencing of transcriptomes enables high depth of
coverage in transcriptome
profiling. However, the resulting gene coverage pattern is far away from
a uniform distribution. This uneven
coverage is partly explained by biases inherent in the experimental
protocols. The term 'uniform
coverage' has been loosely used, without evidence that an unbiased
sequencing experiment results in a
uniform coverage pattern in the mathematical sense. Therefore we ask:
What is a null hypothesis for the
distribution of reads under perfect conditions? We will present a simple
but realistic model that is computationally tractable. Moreover, we will
present a preliminary analyses of real data to
check if predicted patterns do occur. Finally, we will discuss further
applications of the model. This is joint work with Celine Prakash and Stefanie Tauber.
Friday, 20.06.2014, 16ct, V3-204
Holger Schielzeth, Bielefeld University, Faculty of Biology
Animal personality and the predictability of behaviour: mixed
effects models that allow an estimation of between-individual variation
in the variability
Abstract:
Many aspects of animal behaviour differ consistently between
individuals, but while between-individual variation in average trait
values has long been of interest to biologists, the role of
within-individual variation has received much less attention. I will
briefly review the concepts of behavioural plasticity, flexibility,
consistency and predictability and the different indices that have been
used for their quantification. I will then outline hierarchical
generalized linear models (HGLM) and double-hierarchical generalized
linear models (DHGLM) that have been developed in other contexts (in
particular quantitative genetics), but can be adapted to the study of
animal behaviour. A particular aim will be the presentation of an
estimator predictability (the coefficient of variation in
predictability) that can be used for comparisons across studies and
study systems and might thus sever as a comment effect size estimator
for meta-analyses.
Friday, 09.05.2014, 16ct, V3-204
Marc Steinbach, Uni Hannover
Mathematische Optimierung im Gastransport
Abstract:
Mit der Regulierung des europäischen Gasmarktes sind fundamentale
strukturelle Änderungen verbunden, die für Gastransportunternehmen
eine Fülle neuer und hochkomplexer Planungs- und Entscheidungsaufgaben
mit sich bringen.
Der Vortrag geht ein auf Anforderungen aus der Praxis, konkrete
Herausforderungen der mathematischen Formalisierung und Modellierung
sowie auf Optimierungsmodelle und Lösungsansätze, die aus einem
Verbundprojekt mit einem großen Netzbetreiber hervorgegangen sind.
Winter Semester 2013/2014
- Friday, 21.03.2014, 14 ct, U10-146
David Bryant, University of Otago, New Zealand
Phylogenetic analysis of species radiations using SNPs and AFLPs
Abstract:
Technological wonders such as next generation sequencing mean that we can
now, in principle, obtain SNP (single nucleotide polymorphism) data from
multiple individuals in multiple species. This promises enormous benefits
for population genetic and phylogenetic analysis, particularly of closely
related or poorly resolved species. My interest is in how to analyse these
data effectively and responsibly. We have developed an algorithm which
estimates species trees, divergence times, and population sizes from
independent (binary) makers such as well spaced SNPs. The method is
based on coalescent theory (like the BEAST software), though it uses
mathematical trickery to avoid having to consider all the possible
gene trees. As a `full likelihood' method, it should be more accurate
than alternative FST based approaches. I'll talk about our experiences
applying this method to AFLP data from alpine plants, and some recent
discoveries about the usefulness (or uselessness) of SNP data for
estimating population sizes.
- Monday, 02.12.2013, 16 ct, V5-148
L’ubomír Baňas, Bielefeld University
Phase field models for multiphase flow: modelling, numerics and applications
Abstract:
Understanding and accurate prediction of multiphase multicomponent
flows is of essential interest for a large number of
scientific and engineering applications. Despite intensive past and
present research efforts, it is still not clear how to accurately
and efficiently simulate multiphase fluid flow for the full range of
physical parameters and regimes such as, e.g., densities,
viscosities, capillary relations, number of fluid phases, interface
geometry, dynamic or static contact angles, etc.
We review of a promising strategy for the modelling of incompressible
multiphase flow based on the phase-field approach.
We discuss advantages of the approach from the modelling and
computational point of view. We also present a framework
for multiscale flow simulations and discuss applications to multiphase
flow in porous media.
- Tuesday, 19.11.2013, 16ct, H4
D. Shechtman, Technion, Haifa, Israel and ISU, Ames, Iowa, USA
Quasi-periodic materials — crystal redefined
Abstract:
Crystallography has been one of the mature sciences.
Over the years, the modern science of crystallography that started by experimenting with x-ray diffraction from crystals in 1912,
has developed a major paradigm — that all crystals are ordered and periodic. Indeed, this was the basis for the definition of crystal
in textbooks of crystallography and x-ray diffraction. Based upon a vast number of experimental data, constantly improving research tools,
and deepening theoretical understanding of the structure of crystalline materials, no revolution was anticipated in our understanding the
atomic order of solids.
However, such a revolution did happen with the discovery of the icosahedral phase, the first quasi-periodic crystal (QC) in 1982,
and its announcement in 1984 [1, 2].
QCs are ordered materials, but their atomic order is quasiperiodic rather than periodic, enabling formation of crystal symmetries,
such as icosahedral symmetry, which cannot exist in periodic materials. The discovery created deep cracks in this paradigm, but
the acceptance by the crystallographers' community of the new class of ordered crystals did not happen in one day. In fact,
it took almost a decade for QC order to be accepted by most crystallographers. The official stamp of approval came in a form of
a new definition of Crystal by the International Union of Crystallographers. The paradigm that all crystals are periodic has thus been changed.
It is clear now that although most crystals are ordered and periodic, a good number of them are ordered and quasi-periodic.
While believers and nonbelievers were debating, a large volume of experimental and theoretical studies was published, a result of a
relentless effort of many groups around the world. Quasi-periodic materials have developed into an exciting interdisciplinary science.
This talk will outline the discovery of QCs and describe the important role of electron microscopy as an enabling discovery tool.
[1] D. Shechtman, I. Blech, Met. Trans. 16A (June 1985) 1005-1012.
[2] D. Shechtman, I. Blech, D. Gratias, J.W. Cahn, Phys. Rev. Letters, Vol 53, No. 20 (1984) 1951-1953.
- Friday, 15.11.2013, 16ct, V3-204
D. Frettloeh, University Bielefeld
Tilings, pinwheels and quasicrystals
Abstract:
The discovery of quasicrystals by Daniel Shechtman in 1982 kindled a
demand for good models of such solids. An obvious choice are tilings
(tesselations) in 2 and 3 dimensions. Understanding
phenomena occurring in tilings may help to understand phenomena occurring
in quasicrystals or related solids. One interesting such phenomenon is the
ocuurrence of tiles in infinitely many different orientations in simple
deterministic tilings. This talk gives a survey of this phenomenon,
accompanied by several appealing images.
Summer Semester 2013
- Friday, 20.09.2013, 14ct, U10-146
Ulrike Lampe, University Bielefeld
Staying tuned: Developmental plasticity contributes to grasshopper signal adjustment in response to road noise
Abstract:
Rising levels of anthropogenic noise all over the world lead to degradation and masking of
acoustic communication signals, thereby making successful signal transmission in acoustically
communicating species increasingly difficult. It is well-known that man-made noise affects
signal production in different vertebrate taxa. In our earlier work we demonstrated that male
Chorthippus biguttulus grasshoppers from roadside habitats produced courtship signals with
elevated frequency components compared to their conspecifics from rural habitats. Here, we
used a common garden design to study the evolutionary mechanisms behind this effect. We
collected grasshopper nymphs from roadside and rural habitats and transferred them to the
laboratory to rear half of them in a noisy environment (mimicking roadside conditions),
whereas the other half was confronted with a control treatment. Males from roadside
habitats produced signals with higher frequency components compared to males from rural
habitats, thus supporting our previous result. More interestingly, males from the noisy
treatment group produced courtship signals with higher frequencies compared to males from
the control treatment, indicating noise-induced developmental plasticity. Moreover, grasshopper
from roadside habitats produced signals with an increased syllable to pause ratio, possibly
suggesting another strategy to avoid degradation by high background noise levels.
- Monday, 02.09.2013, 14ct, U10-146
Mike Steel,University of Canterbury
Ancestral reconstruction, lateral gene transfer, and the joys of
leaping between trees
Abstract:
In part 1, I will present some recent results with Olivier Gascuel on
how accurately we can expect to predict ancestral states at the
interior nodes of a phylogenetic tree from discrete character data at
the extant leaves.
In part 2, I will describe a second project on
species tree reconstruction when genes have evolved under a simple
model of random lateral gene transfer (LGT). The aim is to answer
questions such as: could we reconstruct a species tree on
(say) 200 species from a large number of gene trees, if each gene has
been laterally transferred into other lineages, on average, ten times?
And can LGT lead to inconsistent tree estimation? Our analysis involves a curious connection to random walks on cyclic graphs.
- Friday, 12.07.2013, 16 ct, in V3-204
Odile Sauzet, University Bielefeld
So einfach ist das! Eine Notwendigkeit in der Medizinische Statistik?
Abstract:
In randomisierten kontrollierten Studien werden meistens zwei (oder mehr)
Gruppen verglichen, und die statistischen Methoden hierfür sind
unkompliziert.
Aber was kann man tun, wenn die „beste“ Methode nicht hilft, um die
Studienergebnisse richtig zu verstehen? Man kann eine andere, neue Methode
entwickeln, die genau diese Fragestellung beantwortet. Aber dann kommen die
Herausforderungen: die Methode muss die „Wahrheit“ (es gibt einen
Unterschied)
zeigen, aber muss verständlich (für einen Nichtstatistiker) und anerkannt
(von Zeitschriftengutachtern) sein. Es ist alles nicht so einfach!
Anhand des
Beispiels von Dichotomisierung einer normalverteilten Variable werden wir
zeigen, wie man eine einfache und (fast) genau „beste“ Methode
entwickeln kann,
um zwei Gruppen zu vergleichen. Damit werden wir die obengenannten
Herausforderungen beantworten.
Summer Semester 2013
- Friday, 28.06.2013, 16 ct, in V3-204
Alan Rendall, University Mainz
Chemical reaction network theory and immunological signalling pathways
Abstract:
Modelling of biological systems often leads to large systems of ordinary
differential equations containing many parameters which are poorly known.
One approach to understanding the global dynamics of solutions of these
systems
is chemical reaction network theory (CRNT). When the results of this theory
apply they give powerful results but it is not clear how widely they can be
expected to be relevant for biological models. After giving an
introduction to
CRNT I will discuss an example (the NFAT signalling pathway) where I was
able
to use the theory to show that all solutions of the system converge to
steady
states at late times. I will also describe an earlier result of Eduardo
Sontag
on the kinetic proofreading model of T cell activation which inspired
this work.
- Friday, 14.06.2013, 16 ct, in V3-204
Noemi Kurt, Technical University of Berlin
Duality of Markov processes: Theory and some population biological
applications
Abstract:
Duality is a powerful tool in the analysis of Markov processes, which
allows
to understand certain aspects of one process (X_t) by analyzing another
process $(Y_t)$ which is dual, meaning that
E_x[H(X_t, y)]=E^y[H(x,Y_t)]
for a suitably large class of duality functions H. Duality has been
applied in a wide range of applications, such as interacting particle
systems, superprocesses, queueing theory, SPDEs and many more, and is
intrinsically connected to concepts like time reversal, stochastic
monotonicity, symmetries and conserved quantities. In this talk, we
present the notion of duality as well as some aspects of existence and
uniqueness of dual processes. We will then turn our attention to monotone
and non-monotone interacting particle systems and their connections via
duality, and explain how such dualities are conserved under rescalings.
Some of the rescaled processes can be understood as population dynamical
models involving various types of selection, and our methods give an
insight on their monotonicity properties.
This is joint work with Sabine Jansen.
- Friday, 24.05.2013, 16 ct, in G2-104
Wolf-Juergen Beyn, Uni Bielefeld
Mathematische Modellbildung, Analyse und Simulation
zellulärer Prozesse
Abstract:
Im Vortrag werden einige Grundprinzipien mathematischer
Modellbildung diskutiert, die zum Verständnis des Zusammenwirkens
zellulärer Einzelprozesse beitragen können.
Zunächst wird auf die verschiedenen Modelltypen eingegangen,
die sich durch Begriffspaare wie diskret-kontinuierlich,
stationär-zeitabhängig, räumlich homogen-inhomogen, linear-nichtlinear und
zufällig-deterministisch unterscheiden lassen.
Speziell werden dann einfache Modellgleichungen für enzymatisch
ablaufende Stoffwechselprozesse analysiert und Möglichkeiten
aufgezeigt, um diese Modelle auf Transportprozesse
und genetische regulierte Netzwerke zu erweitern.
Dabei entstehen oft große Systeme nichtlinearer Differentialgleichungen,
die eine Vielzahl von Parametern enthalten und deren Lösungsverhalten
nicht einfach zu überblicken ist. Einerseits werden solche Systeme
auf dem Computer simuliert und mit experimentellen Daten verglichen,
andererseits versucht man die Modelle so zu reduzieren
(Hauptkomponentenanalyse, Pseudostationarität), dass Einsichten in
biochemisch relevantes Verhalten gewonnen werden können.
- Friday, 26.04.2013, 16 ct, in V3-204
Stefanie Tauber, University of Vienna
Exploring the sampling universe of RNA-seq
Abstract:
How deep is deep enough? While RNA-sequencing represents a well-
established technology, the required sequencing depth for detecting all ex-
pressed genes is not known. If we leave the entire biological overhead and
meta-information behind we are dealing with a classical sampling process.
Such sampling processes are well known from population genetics and thor-
oughly investigated. Here we use the Pitman Sampling Formula to model
the sampling process of RNA-sequencing. By doing so we characterize the
sampling by means of two parameters which grasp the conglomerate of differ-
ent sequencing technologies, protocols and their associated biases. We
differ
between two levels of sampling: number of reads per gene and respectively,
number of reads starting at each position of a specific gene. The latter ap-
proach allows us to evaluate the theoretical expectation of uniform coverage
and the performance of sequencing protocols in that respect. Most impor-
tantly, given a pilot sequencing experiment we provide an estimate for the
size of the underlying sampling universe and, based on these findings, eval-
uate an estimator for the number of newly detected genes when sequencing
an additional sample of arbitrary size.
This is joint work with Arndt von Haeseler.
Winter Semester 2012/2013
- Tuesday, 05.02.2013, 11:15 in U10-146
Andreas Richter,Graphics & Geometry Group,University of Bielefeld
Discrete knot optimization
Abstract:
The topic of this talk is the optimization or unfolding of knots — arbitrary simple closed curves
— toward an as-simple-as-possible and esthetically pleasing shape. Applications can be
found in, e.g., robotics, protein folding, and curve classification. The curve optimization is
performed by numerically minimizing a suitable knot energy, which typically is formulated on
continuous curves and discretized in a second step. In contrast, I present a geometrically intuitive
energy for polygons that is discrete from the beginning. The resulting optimization is
simple to implement, efficient and robust to compute, and yields results of comparable or even
superior quality. In this talk I will discuss general requirements on knot energies, compare several
optimization techniques, and present numerical and (cool) visual results.
Summer Semester 2012
- Friday, June 29th 2012, 16:15 in V3-204
Mike Steel,University of Canterbury, Neuseeland
'Lassoing' a tree: Phylogenetic theory for sparse patterns of taxon coverage
Abstract:
Phylogenomic data often exhibit partial taxon coverage, whereby each
loci is present or sequenced only for some corresponding subset of the
species under study. This leads to some interesting mathematical and
statistical questions as to whether a fully resolved underlying
evolutionary tree for all the taxa can be reconstructed, given perfect
phylogenetic estimates from each locus. We first describe the extent to
which a pattern of taxon coverage can be 'phylogenetically decisive' in
various senses, and provide some applications to data (joint work with
Sanderson and McMahon). We then consider tree reconstruction from
distance data, in settings where accurate estimates of evolutionary
distance exist between only certain pairs of taxa: Does this partial
information suffice to pin down -- or, as we say, 'lasso' -- the
underlying phylogenetic tree? We describe a number of new combinatorial
results concerning lassos (joint work with Dress and Huber), and
conclude with some open problems.
17:15 in V3-204
Jan Manuch, University of British Columbia
Linearization of ancestral chromosomal genomes
Abstract:
Recovering the structure of ancestral genomes can be formalized in
terms of the Consecutive-Ones Property (C1P) of binary matrices.
The corresponding optimization problem asks to extract, from a given
binary matrix, a
maximum subset of rows that satisfy the C1P. This problem is in general
intractable, in particular if the ancestral genome is expected to
contain only linear chromosomes or a unique circular chromosome. In
the present work, we consider a relaxation of these problems, which consists
in allowing genomes that can contain several chromosomes, each either
linear or circular.
We show that, when restricted to binary matrices of degree two (every row
has at most two non zero entries),
used in most ancestral genome reconstruction frameworks,
the problem of recovering an ancestral genome with several circular or
linear chromosomes is
polynomially solvable using a reduction to a matching problem.
We also prove that for degree 3 matrices
the problem is NP-complete, thus tracing sharp tractability
boundaries.
- Friday, April 27th 2012, 16:15 in V3-204
Volker Dürr, Bielefeld
What changes when animals change their movements?
Abstract:
Animals adapt their behaviour to the prevalent requirements posed by
their environment. Quite often, such adaptation of behaviour involves
a change in movement. For example, animals may change gait when
accelerating, or they may engage in distinct movement sequences
as their behavioural goal changes. From a neuroscience point of view,
it is interesting to understand HOW these changes in movement are
being brought about by the nervous system. A prerequisite for
answering this question is the understanding of WHAT actually
changes in the movement, i.e., which parameters are being modified,
or when and how often certain movement motifs occurred before and after
the observed change.
In my talk, I will give an introduction to the scientific approach of natural
movement analysis and explain why I believe that the answer to the WHAT
question is necessary (and not trivial) for the answer of the HOW question
in motor control. For this, I will present examples from at least three
kinds of changes in the movement of insect limbs. First there are
apparent changes that may be explained by properties of the dynamic
system without any trigger for the observed transition in movement.
This includes apparently distinct movement sequences of single legs,
for example during searching or cleaning. Second, there are changes
in coupling strength between adjacent joints. This includes changes
in tactile sampling during near-range exploration. Third, there are
changes in likelihood of certain movement components. This includes
distinct kinds of steps that occur at different times and at different
places during natural, unrestrained walking and climbing.
Winter Semester 2011/2012
- Friday, January 20th 2012, 16:15 in V3-204
Leif Engqvist, Bielefeld
Theoretical approaches to understanding male fertility evolution
Abstract:
When females mate with more than one male, a male reproductive
success will to a large extent be determined by the fertilization
success of his sperm. In this highly competitive situation, sperm with
reduced capacity will only have minute chances to fertilize an egg
cell. Genetic changes causing a decrease in semen quality should
therefore be rapidly swept away by selection. At odds with this view
are many studies demonstrating variation in sperm viability traits in
natural populations. Why do males not manufacture sperm of the highest
possible viability? One reason might be that producing highly viable
sperm is costly. Thus, decreased sperm viability may be advantageous
if males can afford to gain some other benefit. Furthermore, sperm
cells key position in gene transfer between generations makes them
the midpoint of a number of important genetic conflicts. Therefore,
the evolution of optimal fertility might be highly constrained. Here I
will present three recent theoretical models that take these
considerations into account and aim to answer the following questions
regarding male fertility evolution: (1) How is sperm ageing predicted
to be influenced by female mating rate? (2) How does variation in
fertility traits influence male investment in sperm competition? (3)
When does selection lead to variation in fertility and evolution of
alternative reproductive strategies? These analyses reveal some highly
interesting and counterintuitive results that also show that male
strategic investment in sperm traits are often in strong conflict with
female fertility.
- Friday, December 9th 2011, 16:15 in V3-204
Sebastian Steinfartz, Bielefeld
Ökologisch-bedingte adaptive Diversifizierung bei Feuersalamandern
(Salamandra salamandra): eine Herausforderung für "maßgeschneiderte"Simulationsmodelle
Abstract:
Die Entstehung biologischer Vielfalt auf ganz unterschiedlichen
taxonomischen Niveaus ist ein zentrales Forschungsgebiet moderner Evolutionsforschung.
Vor allem die Frage, auf welche Weise und mit welcher Geschwindigkeit neue
Arten entstehen, hat Biologen seit jeher im besonderen Maße fasziniert
und interessiert. Mitteleuropäische, nacheiszeitlich wiederbesiedelte
Lebensraumgemeinschaften eignen sich besonders gut dafür, mögliche
Artbildungsprozesse und deren zugrunde liegenden Mechanismen zu
untersuchen,
da viele der Populationen in diesen Gebieten sich erst vor vergleichsweise
kurzer Zeit (ca. 6000-8000 Jahren) etabliert haben und Anpassungs- und
Diversifizierungsprozesse noch nicht abgeschlossen sind und quasi in situ
beobachtet und untersucht werden können. Die Arbeitsgruppe von Sebastian
Steinfartz untersucht seit etwa 10 Jahren die ökologisch-bedingte
Diversifizierung von Feuersalamander-Populationen im Rheinland mit
besonderem Fokus auf den Kottenforst bei Bonn. Ökologische sowie
populationsgenetische Studien konnten zeigen, dass sich die Feuersalamander
in dieser Population aufgrund der Adaptation an unterschiedliche
Larvalgewässer in zwei genetisch differenzierte Gruppen aufgespalten
haben, und dass dieser Prozess der adaptiven Diversifizierung noch nicht
abgeschlossen ist und eventuell zur Bildung neuer Arten führen könnte.
Im Rahmen des Vortrages soll eine aktuelle Momentaufnahme des Wissenstandes
dieses ökologisch-bedingten Differenzierungsprozesses gezeichnet werden.
Gleichzeitig soll diskutiert werden inwieweit auf diese Population
maßgeschneiderte Simulationsmodelle zum einen die festgestellte
Diversität und Differenzierung erklären können und ob die ökologisch
unterschiedlich angepassten Typen den Artbildungsprozess in Zukunft
abschließen werden oder nicht.
- Monday, November 28th 2011, 17:15 in H6
Prof. Dr. Walter Steurer, ETH Zuerich
Why are quasicrystals quasiperiodic?
Abstract:
To answer this question we have to distinguish between metallic quasicrystals and
quasiperiodic self-assembled colloidal structures. In the latter case special pair potentials
with two different length scales and three-body interactions seem to be the
main driving factors besides entropy. In case of metallic quasicrystals, the underlying
mechanism is quite different. Here, the packing of low-energy clusters with
non-crystallographic symmetry seems to be the decisive factor. The way of overlapping
of these clusters and some other factors lead to a much higher structural
order than in the case of soft quasicrystals. The focus of the talk will be on the ordering
principles of metallic quasicrystals.
- Friday, November 4th 2011, 16:15 in V3-204
Mathias Staudigl, IMW, Bielefeld
Stochastic Stability: Approximation, Convergence and Optimal Control
(joint with William H. Sandholm, University of Wisconsin-Maddison)
Abstract:
In this talk we will discuss some ongoing research on evolutionary
equilibrium selection in games using stochastic methods which are
frequently used in economics. Since the seminal papers of Kandori,
Mailath and Rob (Econometrica, 1993) and Young (Econometrica, 1993)
the Freidlin-Wentzell method to assess the stability of attractors
has been frequently applied in game theoretic models. However, up to
now a satisfactory analysis of these models was restricted to either
very simple strategic situations (i.e. games), or very simple
perturbations of the dynamics. In this talk we will present some new
tools how to overcome these two obstacles by using ideas from stochastic
and deterministic optimal control theory. We will conclude by pointing
out that our methods are not only useful in the study of stochastic
evolutionary game dynamics, but also can be applied to classical
optimization problems, such as Markov decision processes.
This is joint work with William H. Sandholm, University of Wisconsin-Maddison.
Summer Semester 2011
- Friday, July 22nd 2011, 14:15 in U10-146
Michael Kopp, University of Vienna
Adaptation of a quantitative trait to a moving optimum
Abstract:
Biological population can adapt to new environments if established gene variants are
substituted by beneficial mutations, but surprisingly little is known
about the nature of these mutations. Recent modeling efforts have
focused on predicting the distribution of phenotypic effect sizes of
individual substitution events. While the majority of these models
considers adaptation after an abrupt change in the environment, I will
present results for adaptation to gradual environmental change. I will
show that the rate of environmental change can have a strong impact on
the statistical patterns of adaptive substitutions. These results may
help our understanding of evolutionary responses to global change.
- Thursday, July 14th 2011, 10:15 in U10-146
Mareike Fischer, Center for Integrative Bioinformatics, Vienna
Reconstructing evolutionary trees - Chances and pitfalls in modern
phylogenetics
Abstract:
Ever since Darwin published his first sketch of an evolutionary tree in
1859, scientists have been trying to reconstruct the Tree of Life.
Such reconstructions are nowadays usually based on DNA data, which is
interpreted with the help of tree inference methods. Maximum Parsimony
(MP), Maximum Likelihood (ML) and distance-based methods (DB) are three
such methods which are frequently used. In the first part of my talk, I
will introduce MP and DB and I will show that even for the best possible
DNA data, these methods can give contradictory results. In the second
part of my talk, I will focus on the relationship between MP and ML,
which has been widely discussed. For instance, it is well known that
under a simple model of substitution, MP and ML always choose the same
set of trees for DNA sequences. But some surprising properties of MP and
ML have only recently been discovered: I will present examples for MP
and ML favoring different trees when the underlying model is changed
slightly - for example, when substitution probabilities are subject to
an upper bound or when a molecular clock condition is imposed. Finally,
I will show that, even though the two parts of my talk may seem
unrelated at first glance, the same construction idea can be used to
establish both results.
This talk is based on joint work with Bhalchandra Thatte and Hans-Jürgen
Bandelt.
- Friday, June 24th 2011, 16:15 in V3-204
Kristan Schneider, University of Vienna
Genetic Hitchhiking and the Evolution of Anti-Malarial Drug
Resistance
Abstract:
Malaria is among the most devastating human diseases, and it is still a
threat to the public health in large areas of the developing world.
Malaria control is highly dependent on the use of drugs, which clear out
parasites in infected hosts. However, many important drugs have been
rendered useless because parasites evolved resistance against them.
Understanding the evolutionary history of the spread of drug resistance
is the key to extend the lifespan of affordable and reliable
anti-malarial drugs, and hence to guarantee successful malaria control.
However, reconstructing the evolutionary history of drug resistance in
the absence of reliable clinical and epidemiological data is difficult.
Hence, theoretical models that predict the dynamics of the spread of
resistance are urgently needed. While it is difficult to build
mathematical models that consider the full complexity of malaria, we
might be able to reconstruct the dynamics of drug resistance by
analyzing empirical data.
We introduce a model for the spread of drug resistance among human
malaria parasites, which is designed to study genetic hitchhiking. It
incorporates all characteristics of the complex malaria-transmission
cycle and accounts for the fact that only a fraction of infected hosts
receive drug treatment. It also incorporates that hosts can be
co-infected by differently many parasites. The number of parasites
co-infecting a host is either a constant or, more generally, follows a
given frequency distribution.
We show that the hitchhiking effect is similar but different from
standard hitchhiking, and explain why standard hitchhiking theory cannot
be applied to drug resistance in malaria. Furthermore, we show that a
genome-wide reduction in relative heterozygosity occurs provided drug
pressures are sufficiently high and sufficiently many hosts are infected
by single haplotype strains.
- Friday, June 17th 2011, 16:15 in V3-204
Jan de Ruiter, Faculty of Linguistics and Literary Studies, Bielefeld University
Modeling inter-channel dependencies using conditional entropy -- chasing
the illusion of causality.
Abstract:
An intriguing problem in the field of human interaction is the mutual
relationship between multiple signal "channels". An example is social
eye-gaze ("Blickkontakt) and turn-taking.
In order to get a formal handle on this problem, I have captured my
empirical data in a state transition table of a Markov Model, combining
turn-taking and eye-gaze states. This gives us a representation of a)
how much time the communicating dyads spend in each state, and b) what
the transitional probabilities are between different states. This
representation turns out to be surprisingly useful to nail down and test
vague and verbal theories about turn-taking and eye-gaze.
A deeper and more challenging problem is to establish which channel
determines ("dominates") the behavior of the other. It could be that
turn-taking states cause certain patterns in eye-gaze states (as in Adam
Kendon´s 1967 standard theory), but it could also be that eye-gaze
states have an effect on turn-taking states. This leads us to the more
general, but very fishy problem of establishing causality from existing
(historical) data sets, which is impossible for two reasons: first, as
Bertrand Russell and others have convincingly argued, causality does not
exist (except in our minds), and second, it is always possible that what
looks like causality from A to B is actually a correlation between A and
B caused by a third (unknown) factor C. Nevertheless, I am experimenting
with conditional entropy used on partitionings of the transition
probabilities of the Markov model, in an attempt to approximate the
unattainable goal of establishing causality.
Please note that this is work in progress, and not a completed thesis. I
invite everyone to join and contribute to the discussion.
Winter Semester 2010/2011
- Thursday, February 3rd 2011, 14:15 in U10-146
Lorens Imhof, Bonn University
Phenotype Switching and Mutations in Random Environments
Abstract:
Cell populations can benefit from changing phenotype when
the environment changes. One mechanism for generating
these changes is stochastic phenotype switching, whereby
cells switch stochastically from one phenotype to another
according to genetically determined rates, irrespective of
the current environment, with the matching of phenotype to
environment then determined by selective pressure. This
mechanism has been observed in numerous contexts, but
identifying the precise connection between switching rates
and environmental changes remains an open problem. Here we
introduce a simple model to study the evolution of
phenotype switching in a finite population subject to
random environmental shocks. We compare the successes of
competing genotypes with different switching rates and
obtain a characterization of how the optimal switching
rates depend on the frequency of environmental changes in
a symmetric setting. Our results explain why the optimum
is relatively insensitive to fitness in each environment.
This is joint work with Drew Fudenberg.
- Thursday, December 9th 2010, 14:15 in U10-146
Evelyn Herrholz, Hochschule Neubrandenburg
Parsimonious histograms
Abstract:
In the context of one-dimensional density estimation we are faced with
the construction of histograms for given real-valued data. Even if a histogram is
a rather simple density its construction is quite difficult. The number and
width of the bins have to be specified in a satisfactory manner for a wide range of
data sets. Therefore we consider tubes of functions with piecewise constant
boundaries around the empirical cumulative distribution function. It is already
known that the taut string minimizes typical smoothness functionals as well as the
number of modes in such tubes. The latter provides an histogram with minimal
number of local extremes. A related optimization problem is to obtain a histogram
with the smallest number of (unequal length) bins. Its solution is subject of
this talk.
- Thursday, October 21st 2010, 15:00 in U10-146
Marc Hellmuth, Leipzig University
Approximate Graph Products
Abstract:
This talk is concerned with the prime factor decomposition (PFD) of
strong product graphs. A new quasi-linear time
algorithm for the PFD with respect to the strong product for arbitrary,
finite, connected graphs is derived.
Moreover, since most graphs are prime although they can have a
product-like structure, also known as approximate graph products, the
practical application of the well-known "classical" prime factorization
algorithm is strictly limited. This new PFD algorithm is based on a
local approach that covers a graph by small factorizable subgraphs and
then utilizes this information to derive the global factors. Therefore,
we can take advantage of this approach and derive in addition a method
for the recognition of approximate graph products.
- Thursday, October 21st 2010, 14:15 in U10-146
Atheer Matroud, Massey University, Neuseeland
Nested tandem repeats- computation and analysis
Abstract:
Nested tandem repeat (NTR) is a complex repetitive structure, also
referred to as Variable Length Tandem Repeats
by [Hauth and Joseph, 2002]. NTRs structure contains two motifs repeated
and interspersed with each other.
In this presentation I will focus on illustrating some computation and
analysis work I have done on this fascinating repetitive structure,
highlighting the NTR that exists in the Taro plant and its possible use
as a marker for intra-specific population study.
- Thursday, October 14th 2010, 14:15 in U10-146
Arndt Telschow, Helmholtz-Zentrum für
Infektionsforschung, Braunschweig
The role of Wolbachia and other reproductive parasites in eukaryotic
evolution
Abstract:
Reproductive parasites are cytoplasmically inherited
endosymbionts that manipulate the host reproductive system to their own
advantage but to the disadvantage of their host. Common forms of
reproductive parasitism are cytoplasmic incompatibility, male-killing,
feminization, and parthenogenesis induction. Well-studied reproductive
parasites belong to the bacterial groups Wolbachia, Rickettsia,
Spiroplasma, and Cardinia. The wide distribution of these bacteria among
arthropods, with Wolbachia estimated to infect 20-70% of all insect
species, make the study of reproductive parasitism an important topic in
evolution and ecology. In the first part of the presentation, it is
discussed how reproduction parasites modify host gene flow and promote
speciation. A mathematical modelling approach is used and analytical
results for gene flow modification are presented. The results support
the view that Wolbachia can promote host speciation, and, further,
suggest strong impact of reproductive parasites on host gene flow. In
the second part, results from the Nasonia genome project are presented
which suggest horizontal gene transfer between Wolbachia, Nasonia, and
pox viruses. These results suggest an important role of reproductive
parasites in eukaryotic evolution.
Summer Semester 2010
- Thursday, June 10th, 2010, 14:15 in V3-204
Volker Böhm, Bielefeld
On the Dynamics of Asset Prices under Autoregressive
Forecasting and Noise
Abstract:
The talk studies the impact of the interaction of two groups
of heterogeneous investors (so called fundamentalists and
chartists) on the dynamics of asset prices in the capital
asset pricing model (CAPM). Members of both groups apply so
called mean reverting autoregressive forecasting rules.
Forecasts by chartists are made according to an adaptive mean
reverting principle for the first two conditional moments
using past asset price data. Fundamentalists\acute; forecasts also
use a mean reverting process, however, relative to a
perceived so called fundamental value of asset price
assumed to follow a stationary random walk. Different degrees
of mean reversion have a strong impact on the dynamics of
asset prices and returns showing the occurrence of a
Neimark-Sacker bifurcation after a period doubling.
An extensive numerical analysis shows that under these
bifurcations highly cyclical time series of prices and returns
occur which show the three typical features of empirically
observed series of asset prices and returns, insignificant
autocorrelation patterns of prices and returns for high order
lags, which are non decaying for absolute and squared
returns, as well as heavy tailed and skewed
distributions. These results provide evidence that the non
linearities induced by adaptive/autoregressive expectations
are the major cause for overshooting features and fluctuating
asset prices.
The talk extends the analysis to study the impact of
different random influences on aggregate asset supply, asset
dividends, and on the fundamental asset price using numerical
methods. For small enough noise, the period doubling and the
Neimark-Sacker bifurcations are preserved inducing similar
persistent autocorrelations. However, with larger
perturbations and/or group switching, the bifurcations and
autocorrelations disappear showing convergence to stationary
solutions (random fixed points) without significant
autocorrelations.
- Thursday, May 27th, 2010, 14:15 in V3-204
Reinhard Bürger, University of Vienna
Multilocus migration-selection models
Abstract:
Most natural populations are geographically structured and
experience spatially varying selection. We present a general
population-genetic model that incorporates migration between
local populations (demes) and selection acting within demes on
multiple gene loci, each with an arbitrary number of
alleles. The model is formulated in terms of a system of
difference equations and describes the evolution of gamete
frequencies in the demes. In the absence of selection, we
prove global convergence to linkage equilibrium and to spatial
homogeneity. This result is used to derive the weak-selection
limit and to prove generic global convergence of trajectories
if selection is weak relative to migration and
recombination. Analogous results can be proved for the
weak-migration limit and the Levene model.
- Thursday, May 20th, 2010, 14:15 in V3-204
Richard Gardner, Western Washington University
Reconstruction in Geometric Tomography
Abstract:
Geometric tomography is the area of mathematics concerned
with the retrieval of information about a geometric object
from data about its orthogonal projections onto lines or
planes or its intersections with lines or planes. In recent
years, a number of algorithms have been developed for the
purpose of reconstructing convex bodies from data of this
sort. Examples are parallel and point X-rays, width or
brightness functions, and support functions. In each case
the algorithm takes as input a finite number of noisy (that
is, corrupted by error) measurements and outputs a convex
polytope that approximates the unknown convex body. The
algorithms have all been proved to be strongly consistent,
meaning that under suitable conditions, the Hausdorff
distance from the output convex polytope to the unknown body
converges, almost surely, to zero as the number of
measurements increases. In some cases rates of convergence
have also been obtained by applying the theory of empirical
processes.
The talk will survey these results, and briefly mention also
a very recent one concerning reconstruction from
covariograms, functions giving the volume of the
intersection of a convex body with its translates. This
reconstruction problem is closely related to the Phase
Retrieval Problem for characteristic functions of convex
bodies.
The earliest algorithm to be discussed was proposed by
electrical
engineers in 1990, without proof of convergence. The
mathematical methods involve convex geometry and
probability, but the talk is intended to be accessible to a
general audience. The algorithms have been implemented and
pictures of typical computer reconstructions will be
presented.
- Part 1: Thursday, April 29th, 2010, 14:15 in V3-204
Part 2: Thursday, May 6th, 2010, 14:15 in V3-204
Michael Baake, Bielefeld
Diffraction theory of deterministic and stochastic
structures
Abstract:
Mathematical diffraction theory is concerned with the
determination of the diffraction image of a given structure
and the corresponding inverse problem of structure
determination. In recent years, the understanding of systems
with continuous and mixed spectra has improved
considerably. Moreover, the phenomenon of homometry shows
various unexpected new facets. This is particularly so when
systems with stochastic components are taken into account.
This talk reviews some of the recent results, with focus on
concrete examples, and is mainly based on joint work with
U. Grimm and R.V. Moody. In particular, after giving a short
introduction, we will discuss classic deterministic examples
with singular continuous and with absolutely continuous
spectra, and compare the latter with random systems. A
systematic approach is proposed via the theory of stochastic
processes.
Winter Semester 2009/2010
- Friday, March 12th, 2010, 10:15 in V3-204
Götz Gelbrich, Institute for Medical Informatics,
Statistics and Epidemiology, University of Leipzig
Herzinsuffizienz und Depression: Henne und Ei, oder
interagierende Leiden?
Abstract:
Depression hat unter herzinsuffizienten Patienten eine
deutlich erhöhte
Prävalenz, ist mit erhöhter Mortalität verbunden
und hat mit der Schwere der
Herzinsuffizienz eine Reihe klinischer Korrelate. Es wird der Frage
nachgegangen, ob die Depression nur ein Marker für die Progression der
Herzinsuffizienz ist,
oder ob zwischen beiden Erkrankungen durch diverse Pathomechanismen
vermittelte Wechselwirkungen bestehen. Dazu werden anhand eines
Strukturgleichungsmodells längsschnittliche wechselseitige
Beziehungen der Herzinsuffizienz und der Depression untersucht.
- Thursday, February 4th, 2010, 14:15 in V3-204
Thomas Wiehe, University of Cologne
Testing for genomic signatures of adaptive events
Abstract:
Identifying genome sites which underwent recent adaptive evolution -
and distinguishing these genetic from demographic signals - is still
a major challenge in computational population genomics. Here, I will
discuss two approaches, one based on microsatellite variability and
one based on haplotype structure, to address this question.
Furthermore, I will present a method of alignment-free genome
comparison and applications.
- Thursday, January 28th, 2010, 14:15 in V3-204
Eva Buchkremer, Bielefeld
Should I stay or should I go?
Foraging decisions under uncertainty
Abstract:
Experiments testing for variance-sensitivity (also called
risk-sensitivity) usually offer two options delivering identical
expected payoffs, with one option providing a constant and the
other one a variable reward or delay. Animals often show a
preference for the constant option when variance is in amount
(variance-aversion) and a preference for the variable option
when variance is in delay
(variance-proneness). Variance-sensitivity is a taxonomically
widespread phenomenon. Variance-sensitive foraging preferences
contradict predictions derived from evolutionarily-motivated
models that emphasize long-term energetic benefits. We discuss a
new approach of explaining variance-sensitive preferences. We
hypothesize that decision mechanisms are primarily supposed to
ensure optimal responses to the environment in which the animal
forages. This paper demonstrates that simple decision rules
ensure long-term rate maximization and exhibit
variance-sensitive behavior when tested in a classical
risk-sensitivity situation. We also show that behavioral
patterns observed in experiments like preferences for constant
reward amounts and variable time delays are produced by the
decision rules. The decision rules presented here are a first
step towards a decision mechanism that is psychologically
plausible, is advantageous in natural foraging situations and
explains irrational behavior like variance-sensitivity.
- Thursday, January 14th, 2010, 14:15 in V3-204
Jens Stoye, Bielefeld
Rearrangement Models and Single-Cut Operations
Abstract:
At an abstract level, genomes can be compared based on their
gene order, yielding a number of interesting combinatorial and
algorithmical problems. These include the calculation of the
minimum number of rearrangements that are necessary to
transform one genome into another one, where different
rearrangement models have been considered in the past, such as
reversals (REV), Hannenhalli-Pevzner (HP), and Double-Cut and
Join (DCJ). Though each one can be precisely defined, the
general notion of a model so far remained undefined. In this
talk, we give a formal set-theoretic definition, which allows
us to investigate and prove relationships between distances
under various existing and new models. Somewhat surprisingly,
we observe an asymmetry within the space of models we study,
that might be due to an underlying combinatorial structure that
still needs to be elucidated.
This is joint work with Anne Bergeron (Montreal) and Paul Medvedev
(Toronto).
- New date soon...
Reinhard Bürger, University of Vienna
Multilocus migragtion-selection models
Abstract:
Most natural populations are geographically structured and
experience spatially varying selection. We present a general
population-genetic model that incorporates migration between
local populations (demes) and selection acting within demes on
multiple gene loci, each with an arbitrary number of
alleles. The model is formulated in terms of a system of
difference equations and describes the evolution of gamete
frequencies in the demes. In the absence of selection, we prove
global convergence to linkage equilibrium and to spatial
homogeneity. This result is used to derive the weak-selection
limit and to prove generic global convergence of trajectories
if selection is weak relative to migration and
recombination. Analogous results can be proved for the
weak-migration limit and the Levene model.
- Thursday, November 12th, 2009, 14:15 in V3-204
Arndt von Haeseler, University of Vienna
A different view of sequence evolution
Abstract:
Models to describe the evolution of biological sequences abound.
With the increased number of models statistical procedures have
been suggested to select the "best" model
from a large class of typically nested models. While these
procedures are widely used, the Litmus test, whether the best
model really describes the observed data, is typically not
carried out. We will present a method to do exactly
this. Moreover, we will suggest an algorithm that gives a
biologically interpretation to explain the difference between
observed data and predicted data by the model. Several examples
will illustrate the strategy.
This is joint work with Tanja Gesell, Steffen Klaere, and Minh Anh Thi
Nguyen.
- Wednesday, November 4th, 2009, 16:15 in V3-201
Dieter Joseph, Infineon, Munich
Entwicklungen der Patentwelt in Industrie
und Forschung
Abstract:
Ein Erfahrungsbericht aus der Praxis.
Summer Semester 2009
- Thursday, August 27th, 2009, 14:15 in V3-204
Peter Pfaffelhuber, University of Freiburg
Bacterial population genomics
Abstract:
The genome of bacteria is less stable than the genome of
eucariotes. In particular, it is an empirical observation that
bacteria from the same population carry different genes. We study a
model where new genes are introduced from the environment and can be
lost along ancestral lines. By randomizing the genealogy according to
a Kingman coalescent this mutation model, which appears to be new in
the population genetic literature, can be analyzed. Moreover,
empirical data fit well with our theoretical results. This is joint
work with Franz Baumdicker, Wolfgang Hess, University of Freiburg.
- Thursday, July 2nd, 2009, 14:15 in V3-204
Mike Steel, University of Canterbury,
Christchurch, New Zealand
Mixed up trees: The geometry of phylogenetic mixtures
Abstract:
Increasingly complex (and "realistic") models of sequence
evolution carry with them a risk. Namely, as models become more
parameter rich, the ability to accurately infer evolutionary
history from sequence data can decrease unless the additional
parameters can somehow be independently estimated. In extreme
cases two quite different scenarios (e.g. different trees,
or the same tree with quite different branch lengths) can quite
perfectly describe the same data if the background parameters
are adjusted suitably. This talk will describe some fundamental
mathematical limitations in some recent approaches to inferring
evolutionary history, and discuss their relevance for molecular
systematics.
- Thursday, June 25th, 2009, 14:15 in V3-204
Arne Traulsen, MPI for evolutionary biology in Plön
From Game Theory to Populations Genetics (and
back?)
Abstract:
In the past five years, evolutionary game dynamics has made
significant advances by considering finite populations. Many
unexpected and novel results have been obtained that are not
compatible with the usual deterministic framework of
evolutionary game dynamics. The new dynamics is intimately
connected to population genetics, but adds a new perspective
that stresses frequency dependent selection. An important
problem of game theory is the evolution of costly
cooperation among selfish individuals. In population
genetics, this is often described by inclusive fitness
methods. It turns out, however, that the underlying
assumptions are in general very different from the approach
of evolutionary game theory.
-
Tuesday, June 16th, 2009, 18:15 in W9-109
Yeneng Sun, National University of Singapore
Modeling large societies with uncertainty
No abstract available.
- Thursday, May 7th, 2009, 12:30 in V3-201
H.-G. Purwins, Münster
Lokalisierte Lösungen der erweiterten
FitzHugh-Nagumo Gleichungen
Abstract:
Selbstorganisierte dissipative Strukturen sind in Natur und
Technik weit verbreitet und nicht wenige Wissenschaftler sind der
Ansicht, dass deren Verständnis und Anwendung eine der
ganz großen Herausforderungen der modernen
Naturwissenschaften darstellen. Der vorliegende Vortrag
beschäftigt sich mit derartigen Strukturen in der Form
von solitären lokalisierten Spots, die auch
"Dissipative Solitonen" (DSen) genannt werden. Diese Objekte
zeigen in vieler Hinsicht teilchenhaftes Verhalten und
werden sowohl experimentell als auch als Lösungen von
Reaktions-Diffusions-Systemen vom FitzHugh-Nagumo-Typ
beobachtet. Im ersten Teil des Vortrags wird an Hand von
experimentellen elektrischen Transportsystemen dargelegt,
dass DSen z.B. als stationäre und laufende isolierte
Pulse, als stationäre, laufende und rotierende
"Moleküle" und als "kristalline", "flüssige" und
"gasförmige" Vielteilchensysteme auftreten. Die dabei
entdeckten Wechselwirkungsphänomen umfassen sowohl
Streunung und Clusterbildung als auch Generation und
Annihilation. Numerische Untersuchungen zeigen, dass sich
alle experimentellen Beobachtungen qualitativ durch die
verallgemeinerte FitzHugh-Nagumo-Gleichung beschreiben
lassen. Es erweist sich, dass diese Gleichung als eine Art
"Normalform" für eine größere
Universalitätsklasse DSen tragender Systeme betrachtet
werden kann.
Im zweiten Teil des Vortrags wird besprochen, wie sich unter
bestimmten Voraussetzungen aus der verallgemeinerte
FitzHugh-Nagumo-Gleichung Teilchengleichungen ableiten
lassen, die das dynamische Verhalten schwach
wechselwirkender DSen sehr gut beschreiben.
Winter Semester 2008/2009
- Thursday, February 5th, 2009, 14ct in V3-204
Wilfried Gabriel, LMU Muenchen
When is reversible phenotypic plasticity
advantageous?
Abstract:
The ability of a genotype to express different phenotypes in
variable environments often leads to a fitness advantage. Such
adaptive phenotypic plasticity occurs in traits ranging from
morphology to physiology and behavior and can be observed in
nearly all classes of organisms. Understanding the selective
advantage and the limits of plasticity is crucial to numerous
issues in evolution and ecology. Environmental tolerance functions
describe how fitness of an organism depends on the environmental
state. Mode and variance of tolerance functions can be treated as
quantitative genetic traits and its values may be altered if an
organism performs phenotypic plastic changes induced by
environmental cues. Non-plastic, irreversible plastic or reversible
plastic genotypes are favored depending on time pattern and
variance of environmental changes, on the reliability of the
environmental cues, on the time spans needed to perform plastic
shifts and on the costs of plasticity.
- December 12th, 2008 14ct in V3-204
Aernoud van Enter, Uni Groningen
First-order transitions for nonlinear n-vector
models
Abstract:
I discuss the occurrence of first-order transitions in temperature
in various short-range lattice models with a rotation symmetry in d
at least 2. Such transitions turn out to be widespread under the
condition that the interaction potentials are sufficiently
nonlinear. Some extensions to annealed models, and to the
phenomenon of chaotic temperature dependence will be also
discussed.
- November 6th, 2008 14ct in V3-204
Lars Koch, IMW, Bielefeld
Persistent Ideologies in an Evolutionary Setting
Abstract:
We analyse finite two player games in which agents are unable to
verify payoffs. Agents believe in ideologies that specify virtual
payoff matrices of the game. We may, but do not need to assume the
presence of ideologies that are equivalent to the true
payoffs. There may be infinitely many different ideologies present
at the same time. Given ideologies, agents maximize and choose
actions. We define an equilibrium concept and prove existence. We
assume equilibrium play at each point in time, however we refrain
from assuming a particular equilibrium selection. Based on this
setup, we define an evolutionary dynamic on the distribution of
ideologies within the population. In this meta game agents adapt
new ideologies. We assume a monotonic imitation dynamic,
i.e. ideologies that lead to actions which are relatively
successful in terms of true payoffs spread faster in the population
than ideologies that recommend relatively unsuccessful actions. We
characterize the set of stable distributions on the space of
ideologies. For any finite 2 player normal form game we show that
there is an open set of ideologies being not equivalent to the true
payoffs that is not selected against by evolutionary monotonic
dynamics based on the true payoffs of the game. If the game has a
strict equilibrium set, we show stability of non-equivalent
ideologies. We illustrate these results for generic 2X2-games.
- SPECIAL: Lecture series
in context of
"Jahr der
Mathematik"
Mathematik ist überall: Mathematische
Modellbildung
- December 17th, 2008, 18:00 in H13
Klaus Reinhold, Bielefeld
Wie variabel ist die Variabilität biologischer
Merkmale?
- December 8th, 2008, 18:00 in H15(!)
Karl Sigmund, Wien
Zwischen Zwang und Freiwilligkeit:
Die Spieltheorie der Kooperation
- November 26th, 2008, 18:00 in H13
Ellen Baake, Bielefeld
Sind Mutationen spontan oder gerichtet?
Das
Luria-Delbrück-Experiment
- November 12th, 2008, 18:00 in H13
Frank Riedel, Bielefeld
Total smart und auch noch reich - hohe Mathematik in der
Wirtschaft
- October 29th, 2008, 18:00 in H13
Philippe Blanchard, Bielefeld
Komplexe Netzwerke und zufällige Graphen in und jenseits
der Physik
(For abstracts visit
"Jahr der
Mathematik")
Summer Semester 2008
- July 2nd, 2008
Werner Kirsch, Hagen
Mathematik und Politik: Von Macht, Ministern und
Quadratwurzeln
Abstract:
Die Frage nach einer angemessenen Vertretung aller Beteiligten am
demokratischen Entscheidungsprozess ist eine der Grundfragen der
Demokratie. So haben zum Beispiel im Ministerrat der
Europäischen Union die Mitgliedsstaaten - je nach ihrer
Bevölkerungsgröße - unterschiedlich viele
Stimmen. Immer wieder gibt es bei Gipfeltreffen der EU Streit und
Gezerre um diese Stimmgewichte; erst im vergangenen Jahr
überraschte die polnische Regierung die Öffentlichkeit
mit ihrer Forderung nach der "Quadratwurzel-Verteilung" der
Stimmen. Ähnliche Probleme ergeben sich bei anderen
internationalen Organisationen (Weltbank, UNO), bei
Länderkammern, wie dem Bundesrat, oder bei der Machtverteilung
in großen Wirtschaftsunternehmen (z.B. VW).
Kann man
solche Machtverteilungen mit Hilfe der Mathematik analysieren? Ist
es möglich, mit mathematischen Methoden eine Stimmverteilung
als besonders "gerecht" auszuzeichnen? Der Vortrag wird
versuchen, diese Fragen zu beantworten und Denkanstöße
für die politische Praxis zu liefern.
Dieser Vortrag ist
der Auftakt zu einer Veranstaltungsreihe im Rahmen des Jahres der
Mathematik mit dem Titel "Mathematik ist überall:
Mathematische Modellbildung". Diese Reihe wird im Wintersemester
fortgesetzt.
- July 1st, 2008
Mike Steel, Christchurch, New Zealand
The Joys of Being Mean: Tricks for (Evolutionary) Trees
Abstract:
I describe how one can sometimes obtain useful insights into
the
properties of phylogenetic models -- both old and new -- that at first
seem quite complex, by exploiting standard properties of expectation
(the "mean" of an appropriate random variable).
- April 24th, 2008
Tanja Gernhard, TU Munich
A statistic for detecting lineage-specific bursts in a tree
Abstract:
In this talk I discuss tree statistics. First, the most common tree
statistics are reviewed. We will see that lineage-specific speciation
bursts cannot be detected with those statistics. I present a new statistic
summarizing the timing of branching events, the runs statistic, which
detects lineage-specific bursts. The statistic is applied to two example
applications: we show that the evolution of the Hepatitis C virus appears
to proceed in a lineage-specific bursting fashion; the ant phylogeny
shows a speciation burst, but there is no evidence for lineage-specific
bursting.
Winter Semester 2007/2008
- January 31st, 2008
Joachim Krug, University of Cologne
Adaptation dynamics in smooth and rugged fitness landscapes
Abstract:
The talk will begin by briefly introducing
key concepts of population genetics such as fitness landscapes,
sequence space and fixation in the context of the Wright-Fisher model for
the asexual evolution of finite populations, which provides a basic
description of evolution experiments with bacteria and viruses.
I then identify the parameters which allow for a broad classification
of evolutionary regimes in rugged fitness landscapes with many peaks [1],
and provide a detailed analysis of the phenomenon of clonal
interference in a smooth (non-epistatic) landscape [2]. Finally, I
will describe recent work on the house-of-cards model in finite
populations [3], which is the simplest realization of a fitness
landscape with strong epistasis. The talk is based on joint
work with Kavita Jain and Su-Chan Park.
[1] K. Jain, JK, Genetics 175, 1275 (2007)
[2] S.C. Park, JK, PNAS 104, 18135 (2007)
[3] S.C. Park, JK, submitted to JSTAT (arXiv:0711.1989)
- December 13th, 2007
Eva Maria Griebeler, University of Mainz
Effekte der globalen Temperaturerhöhung auf die
Populationsdynamik von Arten am Beispiel der Westlichen
Beißschrecke (Platycleis albopunctata) und der
Dreikantmuschel (Dreissena polymorpha)
Abstract:
Die globale Klimaveränderung wird die Habitate vieler Arten
dramatisch verändern. Falls es ihnen nicht gelingt sich an die
geänderten Umweltbedingungen anzupassen, werden sie
möglicherweise langfristig aussterben. In meinem Vortrag möchte
ich den Effekt von Temperaturerhöhung auf die Populationsdynamik
exemplarisch für eine terrestrische und eine aquatisch lebende
Art analysieren. Freilandstudien haben gezeigt, dass sowohl die
Westliche Beißschrecke (Platycleis albopunctata) als auch die
Dreikantmuschel (Dreissena polymorpha) in Habitaten mit sehr
unterschiedlichen Temperaturbedingungen überleben können. Man
kann daher vermuten, dass die beiden Arten auch unter der
zukünftig zu erwartenden Temperaturerhöhung überleben
werden. Diese Hypothese habe ich mit Hilfe von zwei
Simulationsmodellen überprüft.
- December 4th, 2007
Achim Klenke, University of Mainz
Infinite Rate Mutually Catalytic Branching
Abstract:
In 1998 Dawson and Perkins introduced a model of continuous
state mutually catalytic branching on some countable Abelian
group 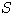 as
site space. At each
colony
as
site space. At each
colony 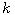 at
time
at
time 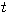 there
is a continuous amount
there
is a continuous amount 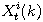 of particles of
type
of particles of
type 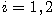 . Time evolution is governed by
. Time evolution is governed by
-
migration on
 according to some symmetric random walk
kernel
according to some symmetric random walk
kernel 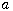 ,
,
-
random fluctuations of each type that are modelled locally by
Feller´s branching diffusion but at a rate proportional to the
mass of the respective other type.
Formally, the evolution can be described by a system of
stochastic differential equations,
![$$ dX^i_t(k)=\sum_{l\in
S}a(k,l)\big[X_t^i(l)-X^i_t(k)\big]dt
+\sqrt{\gamma X1_t(k)X2_t(k)\,}dW^i_t(k),$$](formulas/klenke-eq1.png)
where 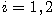 ,
,
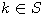 ,
,
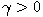 is
a parameter, and
is
a parameter, and
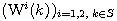 is an independent
family of Brownian motions.
is an independent
family of Brownian motions.
For the investigation of the longtime behaviour of this model it
is useful to understand the limit model of
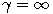 .
In a first step we construct this limit model via a martingale
problem involving a Lévy-type jump measure on the state space
.
In a first step we construct this limit model via a martingale
problem involving a Lévy-type jump measure on the state space
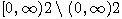 of each colony.
In a second step we derive a sufficient condition for global
coexistence of both types when started from a finite initial
state. We show that it is sufficient that
of each colony.
In a second step we derive a sufficient condition for global
coexistence of both types when started from a finite initial
state. We show that it is sufficient that
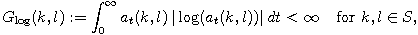
where  is the
continuous time kernel of the
is the
continuous time kernel of the
 -random walk,
and
-random walk,
and
- the initial masses of type 1 and 2 are placed at sites
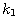 and
and
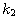 such
that
such
that
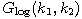 is small.
is small.
In contrast, for the
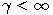 model, Dawson and Perkins
showed that for coexistence of types the weaker condition that
model, Dawson and Perkins
showed that for coexistence of types the weaker condition that
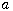 is transient is necessary and sufficient.
is transient is necessary and sufficient.
This is joint work with Leonid Mytnik.
- October 25th, 2007
Joachim Krug, University of Cologne
Adaption dynamics in smooth and rugged fitness
landscapes
Abstract:
The talk will begin by briefly introducing key concepts of
population genetics such as fitness landscapes, sequence space and
fixation in the context of the Wright-Fisher model for the asexual
evolution of finite populations, which provides a basic description
of evolution experiments with bacteria and viruses. I then identify
the parameters which allow for a broad classification of
evolutionary regimes in rugged fitness landscapes with many peaks
[1], and provide a detailed analysis of the phenomenon of "clonal
interference" in a smooth (non-epistatic) landscape [2]. The talk
is based on joint work with Kavita Jain and Su-Chan Park.
[1] K. Jain, JK, Genetics 175, 1275 (2007)
[2] S.C. Park, JK, PNAS (in press)
Summer Semester 2007
- June 18th, 2007
Marc Steinbach, University of Hannover
Nonlinear Optimization on Scenario Trees
Abstract:
Multistage stochastic programming models are becoming vital in
decision support for planning under uncertainty in various
areas. While linear scenario tree models are widely used, well
understood, and tractable by (almost) mature large scale
optimization codes, comparably well developed solvers for nonlinear
models do not yet exist. We present an approach that combines a
suitable interior point method (handling nonlinearity and
nonconvexity) with a "tree-sparse KKT solver" for the expensive
linear-indefinite Newton step subproblems (handling the excessive
size of multistage models by exploiting their rich structure). The
approach is motivated and illustrated with examples from portfolio
optimization, robust process control, and electricity trading, for
which computational results will be presented.
- June 14th, 2007
Iwan Jensen, Melbourne University
Exact solutions for models of punctured staircase polygons
Abstract:
In many cases real life phenomena are modelled by simplified
solvable models, which despite the simplifications can give us
great insight into the behaviour of the more complicated
fully-fledged problem. A well-known long standing problem in
statistical mechanics is to find the perimeter generating function
for self-avoiding polygons on two-dimensional lattices. Several
simplifications of this problem are solvable, but all the simpler
models impose an effective directedness or other constraint that
reduces the problem, in essence, to a one-dimensional problem. A
very important and interesting insight gained from these simple
models (staircase polygons in particular) is a conjecture for the
limit distribution of area and scaling function for self-avoiding
polygons. Here we report on the discovery of the exact perimeter
generating function for two models of punctured staircase
polygons. We started by counting the exact number of punctured
polygons. Using this series we found that all the terms in the
generating function can be reproduced from a linear Fuchsian
differential equation. In one case we managed to solve the ODE and
find a closed form expression for the generating function. We have
since been able to prove this results exactly using combinatorial
arguments. This solution allows a generalisation to a model with
any fixed number of nested punctures as well as to other types of
polygons. This is joint work with Andrew Rechnitzer (University of
British Columbia), Mike Zabrocki (York University) and Anthony
Guttmann (Melbourne University) and contains significant results
from work with Christoph Richard.
- May 24th, 2007
Frank Riedel, Bielefeld University
Evolutionary Game Theory - Theory and Applications
for Continuum Strategy Models
Abstract:
We give an overview of evolutionary reasoning in Game Theory,
with a special emphasis on games with a continuum of
strategies. Whereas traditional game theory relies on the concepts
of rationality, common knowledge and Nash equilibrium, evolutionary
models use only the forces of selection and mutation to decsribe
long run outcomes in games. Interestingly, the "folk theorem of
evolutionary game theory" shows that stable states of such
dynamics frequently are (very robust) Nash equilibria. In this
sense, evolution leads to rationality. The talk discusses in which
sense this can be rationalized to games with a continuum of
strategies.
- May 10th, 2007
Carmen Molina-Paris, University of Leeds
Peripheral T cell repertoire maintenance -- the
quasi-stationary distribution
Abstract:
A healthy immune system requires a T cell population that responds
promptly to foreign antigen. This is achieved by using a variety of
self-peptides to (i) select a receptor repertoire in the thymus and
(ii) keep naive T cells alive and ready for action in the
periphery. In this talk I will present a stochastic mathematical
model to study T cell repertoire diversity maintenance. The model
incorporates the concept of survival stimuli emanating from self
antigen presenting cells. I will show that in the mean field
approximation clonotype extinction is guaranteed and compute
extinction times of T cell clonotypes without thymic input. I will
introduce the concept of the mean niche overlap and make use of the
quasi-stationary distribution to compute average clonotype numbers
for different values of the niche overlap.
- April 5th, 2007
Bernd Kugelmann, University of Greifswald
Optimale Steuerung am Beispiel von Fischfangquoten
Abstract:
Im Vortrag wird ein Modell für die zeitliche Entwicklung von einer
oder mehrerer Fischpopulationen in der Ostsee unter dem Einfluss
von Erntemaßnahmen vorgestellt. Diese Fangbemühungen sollen so
gesteuert werden, dass ein rein ökonomisches Zielkriterium
optimiert wird. Mit steigender Komplexität des Modells wird die
analytische Lösung des Problems immer schwieriger. Im Vortrag wird
eine Methode zur numerischen Lösung dieses
Optimalsteuerungsproblems erläutert und die Ergebnisse werden
diskutiert.
Winter Semester 2006/2007
- January 23rd, 2007
Erwin Frey, Ludwig-Maximilians-Universität Munich
Soft Materials and Collective Phenomena in Cellular Systems
Abstract:
Rapid developments in molecular biology and single molecule methods
have provided evidence that soft interactions and fluctuation
phenomena play a vital role in biology, in particular on the level
of the very fundamental processes such as cytoskeletal
organization, force generation by molecular motors, and cell
motility.
In this talk I will review our understanding of fibrous materials that
are ubiquitious in nature, and collective phenomena which may arise
in intracellular transport processes. The elastic properties of
fibrous biomaterials result from a subtle interplay between the
architecture of the network and the elastic properties of its
building blocks. A description of these systems requires novel
concepts in polymer physics. Brownian motion governs the transport
along molecular multi-lane highways in cells. Exploring these
systems´ behavior, we find that it can be tuned by controlling
particle fluxes at the boundaries and the bulk of the track. In
addition to their biological relevance these systems may also be
viewed as novel nonequilibrium devices.
- January 18th, 2007
Marc Timme, Max Planck Institute for Dynamics and
Self-Organization and Bernstein Center for Computational
Neuroscience Göttingen
Speed Limits in Spiking Neural Networks Explained by
Random Matrix Theory
Abstract:
Precisely coordinated spatio-temporal spiking dynamics have been
observed experimentally in different neuronal systems and are
discussed to be an essential part of computation in the
brain. Their dynamical origin, however, remains unknown.
Here we study the dynamics of neural network models and reveal basic
mechanisms underlying the neurons´ precise temporal
coordination. We focus on the synchronization dynamics of neural
networks exhibiting a complicated connection topology. In such
networks, an irregular, balanced state coexists with a synchronous
state of regular activity. Using a random matrix approach we
predict the speed of synchronization in such networks in dependence
of properties of individual neurons and their interaction
network. We find that the speed of synchronization is limited by
the network connectivity and remains finite, even if the coupling
strengths between neurons become infinitely large. We offer an
intuitive explanation of this phenomenon.
- January 15th, 2007
Hans-Otto Georgii, University of Munich
The two-dimensional Ising model: What can we learn
from its typical configurations?
Abstract:
The Ising model on the square lattice Z^2 is a primary example of a
statistical mechanics model showing phase transition. The interplay
between its local and global behaviour is clearly displayed by the
random geometry of clusters appearing in its typical
configurations. In conjunction with the attractiveness and
nearest-neigbour character of the interaction, this geometry allows
a detailed analysis of the possible equilibrium states. In
particular, it follows that - at any temperature - there exist
either one or two extremal equilibrium states. The talk will give
an introduction to the model and describe some central results and
techniques.
- December 7th, 2006
Sven Wiesinger, Bielefeld University
Two mathematical models for stochastic
resonance in an asymmetric double-well potential
Abstract:
After an introduction to the concept of stochastic resonance and
some notes about applications, the talk will concentrate on an
overview of two mathematical approaches to stochastic resonance in
an asymmetric double-well potential: The classical approach, based
on the Freidlin-Wentzell theory for random perturbations of
dynamical systems, and a newer approach based on research results
by N. Berglund and B. Gentz.
Summer Semester 2006
- August 21st, 2006
Ulrich Gerland, LMU Munich
Physical, functional, and evolutionary aspects of
transcription factor-DNA interaction
Abstract:
To regulate the transcription of a gene, one or more transcription
factors bind to closeby sites on the DNA, which they recognize
through their specific sequences. The aim of this talk is to
illustrate how the physical process of target site location and
discrimination from the genomic background is entangled with the
biological function. This interplay of physics and function can
also shed some light on the evolutionary aspects of these
interactions.
- August 3rd, 2006
Jay Taylor, Oxford University, U.K.
The common ancestor process via diffusion theory
Abstract:
One strategy for incorporating population genetic processes into a
phylogenetic framework is through the common ancestor process,
which describes the sequence of mutations along the unique lineage
from which all extant individuals are descended. Although the
common ancestor process in a population evolving according to a
multitype branching process has been studied in some depth (e.g.,
Georgii and Baake (2003)), analysis of the CAP for a population of
constant size is complicated by the lack of independence between
individuals. In particular, if there are fitness differences
between individuals, then the CAP fails to satisfy the Markov
property. Fearnhead (2002) was able to characterize the CAP for a
population with two fitness classes using the ancestral selection
graph, obtaining a Markov process by introducing a family of
virtual lineages representing those necessarily out-competed by the
common ancestor (which is guaranteed to survive for all time).
In this talk we will describe an alternative characterization of
the common ancestor process using the coupled allele
frequency-coalescent process introduced by Kaplan, Darden and
Hudson (1988). Here we obtain a Markov process by keeping track not
only of the type of the common ancestor but also of the frequencies
of the types segregating in the population. We show that our
results complement those obtained by Fearnhead in the case of
constant fitnesses. In addition, the diffusion theoretic approach
readily extends to other one-dimensional population genetic models
and we use it to study the common ancestor process in populations
subject to frequency-dependent selection, fluctuating selection,
and bottlenecks.
- July 18th, 2006
Mike Steel, University of Canterbury, Christchurch,
New Zealand
Combinatorial approaches in phylogenetics
Abstract:
Phylogenetics is the reconstruction and analysis of "evolutionary"
trees and graphs in biology (and related areas of classification,
such as linguistics). Discrete mathematics plays an important role
in the underlying theory. We will describe some of the ways in
which concepts from combinatorics (e.g. poset theory, greedoids,
cyclic permutations, Menger´s theorem, closure operators, chordal
graphs) play a central role. As well as providing an overview, we
also describe some recent and new results, and outline some open
problems.
- July 6th, 2006
Ellen Baake, Bielefeld University
Der Gordische DNA-Knoten: Enzymscheren und Geometrie
Abstract:
Im Laufe des Lebens einer Zelle wird ihre DNA mehrfach verknäult und
wieder entwirrt. Dafür verantwortlich sind gewisse Enzyme,
sogenannte Topoisomerasen, die, wie der Name schon sagt, bestimmte
topologische Operationen an DNA-Molekülen durchführen. Ihre
Funktionsweise wurde in enger Kooperation zwischen Biochemikern und
Mathematikern aufgeklärt; wesentliches Werkzeug war dabei der Satz
von White zur Geometrie von Bändern.
Der Vortrag gibt einen Überblick über diesen "Klassiker" der
mathematischen Biologie.
- June 27th, 2006
Gaby Schneider, University of Frankfurt
A stochastic model for near-synchronous neuronal firing activity
Abstract:
The precise timing of the firing of cortical neurons may be central
for information processing in the brain. Recently, very small
delays have been discovered between pairs of neurons, invisible in
the raw processes but detectable in their cross correlation
function. A stochastic model for the parallel firing activity of
multiple neurons is presented which offers a possible explanation
for the mechanism of the observed delays.
- June 22nd, 2006
Jochen Blath, TU Berlin
Lambda-Coalescents as stochastic models in population
genetics:
Are they really out there?
Abstract:
Stochastic processes form a cornerstone of quantitative population
genetics. Of particular interest in this talk are so-called
coalescent processes, which can be used to model the genealogical
tree of a population.
Since their introduction in 1999, the structure of so-called
Lambda-Coalescents and of their corresponding
population models, the generalised Fleming-Viot
(super-)processes, has been thoroughly studied. Special
cases, e.g. Beta-coalescents with Beta strictly between 1 and 2,
allowing multiple genealogical mergers, can be considered as models
for the genealogy of populations with rather extreme reproductive
behaviour, in so far as, e.g., single individuals are able, within
a single reproductive step, to produce a number of offspring
potentially of the same order of magnitude as the size of the
original population.
However, for the genealogy of many populations (in the domain of
attraction of the so-called classical Fleming-Viot process), the
reasonable (and very succesful) standard model in population
genetics is KingmanŽs Coalescent, which allows binary genealogical
mergers only. Methods developed on the basis of this model admit,
e.g. via importance sampling or MCMC methods, efficient
likelyhood-based inference of evolutionary parameters from
relatively large samples in population genetics.
Recently, Eldon and Wakely provided evidence that the Kingman
Coalescent as traditional null-model, in certain situations
(e.g. for some marine species), might need to be replaced by more
general models, since such species do exhibit the extreme
reproductive behaviour described above.
In a joint project with Matthias Birkner (WIAS Berlin), we address
the question whether, how and which Lambda Coalescents can provide
better models as basis for fully likelihood based inference in such
situations.



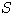 as
site space. At each
colony
as
site space. At each
colony 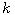 at
time
at
time 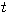 there
is a continuous amount
there
is a continuous amount 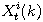 of particles of
type
of particles of
type 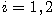 . Time evolution is governed by
. Time evolution is governed by
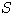 according to some symmetric random walk
kernel
according to some symmetric random walk
kernel 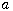 ,
,
![$$ dX^i_t(k)=\sum_{l\in
S}a(k,l)\big[X_t^i(l)-X^i_t(k)\big]dt
+\sqrt{\gamma X1_t(k)X2_t(k)\,}dW^i_t(k),$$](formulas/klenke-eq1.png)
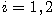 ,
,
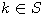 ,
,
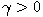 is
a parameter, and
is
a parameter, and
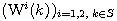 is an independent
family of Brownian motions.
is an independent
family of Brownian motions.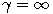 .
In a first step we construct this limit model via a martingale
problem involving a Lévy-type jump measure on the state space
.
In a first step we construct this limit model via a martingale
problem involving a Lévy-type jump measure on the state space
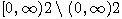 of each colony.
In a second step we derive a sufficient condition for global
coexistence of both types when started from a finite initial
state. We show that it is sufficient that
of each colony.
In a second step we derive a sufficient condition for global
coexistence of both types when started from a finite initial
state. We show that it is sufficient that
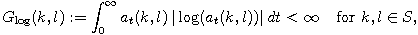
 is the
continuous time kernel of the
is the
continuous time kernel of the
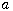 -random walk,
and
-random walk,
and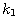 and
and
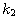 such
that
such
that
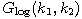 is small.
is small.
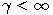 model, Dawson and Perkins
showed that for coexistence of types the weaker condition that
model, Dawson and Perkins
showed that for coexistence of types the weaker condition that
 is transient is necessary and sufficient.
is transient is necessary and sufficient.