Aufgabe 3.7.3
Es sollte gezeigt werden, dass 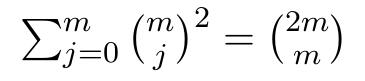 .
Das ist per Induktion (so war es gedacht) schwierig bis unmöglich.
.
Das ist per Induktion (so war es gedacht) schwierig bis unmöglich.
Googlen wir "sum square binomial coefficient", dann finden wir einige
Beweise.
Hier steht ein kombinatorischer ("Kombinatorik": die Kunst, Dinge zu zählen)
Beweis und ein Beweis per vollständiger Induktion. Der Induktionsbeweis ist
aber ziemlich lang, und dennoch benutzt er zwischendurch die
Chu-Vandermonde-Gleichung.
Allerdings ist unsere Aussage sowieso nur ein Spezialfall der
Chu-Vandermonde-Gleichung: setze m=n, r=n und beachte,
dass (n über n-k) gleich (n über k) ist.
Finden wir also einen Beweis für die Chu-Vandermonde-Gleichung, so
haben wir auch einen Beweis für unsere Gleichung. Wikipedia liefert
gleich
drei
Beweise für die Chu-Vandermonde-Gleichung. Allerdings keinen per
vollständiger Induktion.
Der "algebraic proof" benutzt nur den Binomischen Lehrsatz (den hatten wir)
sowie das Produkt zweier endlicher Summen (hatten wir so nicht behandelt,
kann man sich mit etwas Geduld überlegen). Auf sowas selbst zu kommen ist
allerdings ziemlich schwierig, das ist hohe Kunst. Ich persönlich wäre
nie auf diesen Beweis gekommen (höchstens auf den "geometrical proof").
Der "combinatorial proof" ist besonders einfach (zu verstehen, nicht zu
finden! Ich selbst hätte den auch nicht gefunden).
Dazu müssen wir eigentlich nur wissen, dass es n über
k Möglichkeiten gibt, k Leute aus n Leuten auszuwählen.
Dann zählen wir auf zwei Weisen die Anzahl der verschiedenen Möglichkeiten,
aus einer Menge von m Männern und n Frauen ein Komitee mit r Mitgliedern
auszusuchen. Das ist einmal einfach (m+n über r). Zum anderen
ist das auch die Summe der folgenden Möglichkeiten: 0 Männer und r Frauen
wählen, 1 Mann und r-1 Frauen wählen... bis r Männer und 0 Frauen wählen.
Für das erste gibt's (m über 0) mal (n über r)
Möglichkeiten,
für das zweite gibt's (m über 1) mal (n über r-1)
Möglichkeiten,
usw. bis für das letzte gibt's (m über r) mal (n über
0) Möglichkeiten.
Diese Summe ist die Anzahl der Möglichkeiten, m+n
über r ist auch die Anzahl der Möglichkeiten, also müssen die
beiden übereinstimmen.
Für die Lösung dieser Aufgabe hatte ich eine Flasche Wein versprochen.
Das gilt jetzt natürlich nur noch für Lösungen, die nicht hier aufgelistet
sind.
Zuletzt geändert am 24.9.2014
Dirk Frettlöh
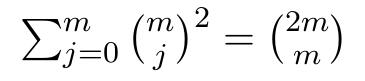 .
Das ist per Induktion (so war es gedacht) schwierig bis unmöglich.
.
Das ist per Induktion (so war es gedacht) schwierig bis unmöglich.