Bielefeld Analysis Seminar
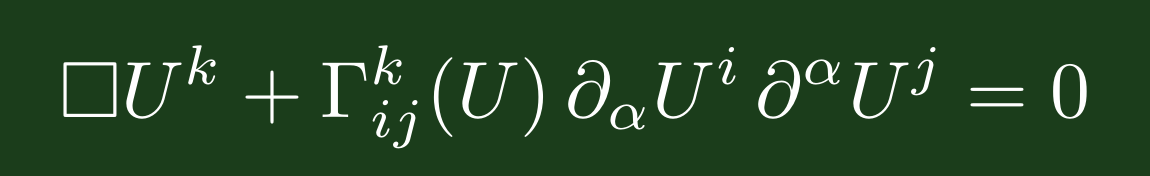
Organizers: Sebastian Herr, Matthias Erbar, Irfan Glogić
Location: Bielefeld University, Room U5-133
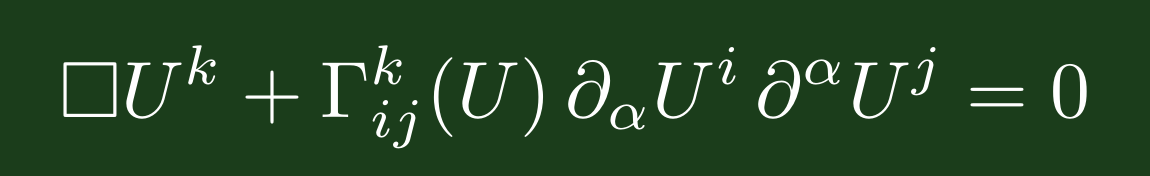
Organizers: Sebastian Herr, Matthias Erbar, Irfan Glogić
Location: Bielefeld University, Room U5-133
Group members working remotely, as well as the general audience, can participate via the Zoom link we provide for each talk.
Metric graphs are networks obtained by gluing together intervals at their endpoints. Once a Laplacian is defined on such metric measure spaces, it becomes natural to investigate the corresponding gradient flows: two different spaces are especially natural, and they will both be discussed in this talk. In particular, these gradient flows are associated with a heat kernel: I will present some recent results relating the short-term asymptotics of this heat kernel and the geometry of the underlying metric graph.
Join Zoom Meeting
Meeting ID: [639 2876 8344]
Password: [054853]
SIn this talk I will discuss the convergence of spatial discretizations for reaction-diffusion systems with mass-action law satisfying a detailed balance condition.
Considering systems on the \(d\)-dimensional torus, we construct appropriate space-discrete processes and show convergence not only on the level of solutions, but on the level of the gradient systems governing the evolutions. As an important step, we prove chain rule inequalities for the reaction-diffusion systems as well as their discretizations, featuring a non-convex dissipation functional. The convergence is obtained with variational methods by building on the recently introduced notion of gradient systems in continuity equation format. Finally, I will highlight how space-discrete processes can also be used to approximate nonlinear cross-diffusion systems with size exclusion on the gradient systems level.
The talk is based in part on joint work with Alexander Mielke and Artur Stephan.
Sharp Strichartz estimates for 2D (hyperbolic) Schrodinger in the whole space follows from dispersive estimates and by now standard \(TT^{*}\) argument. It is not easy to generaliz such a proof to the torus or waveguide case. We will present another proof of such estimates in the whole space case, which will actually yield end point \(L^4\) Strichartz estimates for hyperbolic Schrodinger on wave guide with no derivative loss. This is joint work in preparation with Deng, Zhao (BIT).
Wind-generated currents play a crucial role in the
near-surface oceanic circulation. They are characterised by a three-way
balance between the horizontal pressure gradient, the Coriolis force,
and the horizontal stress that arises through turbulent motion due to
the overlying wind. Historically, the first model that successfully
captured the main qualitative properties of wind-drift currents was
proposed in 1905 by V. W. Ekman, as an attempt to explain seemingly
counter-intuitive observations made by Fridtjof Nansen during the
latter's celebrated _Fram_ expedition of 1893-1896. In this talk, after
some brief historical remarks, I will present the key aspects of the
derivation and properties of a more general and consistent model for
these flows, beyond Ekman's classical model. Then, I will discuss some
properties of solutions to this model and give an outlook on possible
directions of future research. This is ongoing work with Christian
Puntini (Universität Wien).
Hyperbolic balance laws crop up in many physical theories including compressible fluid dynamics, electromagnetism, and general relativity. More abstractly, they play a role in models featuring wave phenomena. If nonlinear, these systems are prone to singularity formation, meaning that even small data with high regularity can launch solutions that blow up in finite time. As it turns out, such behavior is generic for conservation laws in low dimension. However, with an appropriate damping source, the formation of singularities like shocks is suppressed for sufficiently small data. In this talk we will discuss how expanding spacetimes, as found in cosmology, can create such a damping effect and explore the dynamics of these competing mechanisms.
In this talk, we explore the long-time dynamics of solutions to nonlinear Dirac-type equations across several regimes. In one dimension, we show that every global \(L^2\) solution of the massless Dirac equation decays to zero in time within a region expanding at a rate proportional to \( \log^{-2} t \), without any smallness assumptions on the initial data or restrictions on the power of the nonlinearity. This rules out the existence of localized, oscillatory, or breather-like structures in this setting.
These methods extend to three dimensions, yielding decay under boundedness of the \(H^1\) norm on certain partial wave subspace. Finally, in arbitrary dimensions, we establish \(L^2\) decay in the exterior of the light cone, confirming that nonlinear Dirac fields cannot support superluminal propagation. The analysis is driven by a family of weighted virial identities that reveal the dispersive structure of the Dirac operator.
If time permits, we will also discuss recent progress toward the two-dimensional case.
This talk is based on joint work with S. Herr and C. Muñoz.
Gibbs measures for nonlinear dispersive PDEs have been used as a fundamental tool in the study of low-regularity almost sure global well-posedness of the associated Cauchy problem following the pioneering work of Bourgain in the 1990s. In the first part of the talk, we will discuss the connection of Gibbs measures with the classical Kubo-Martin-Schwinger (KMS) condition. The latter is a property characterizing equilibrium measures of the Liouville equation. In particular, we show that Gibbs measures are the unique KMS equilibrium states for a wide class of Hamiltonian PDEs, including nonlinear Schrödinger equations with defocusing interactions. Our proof is based on Malliavin calculus and Gross-Sobolev spaces. This is joint work with Zied Ammari (University of Besançon, Bourgogne-Franche-Comté).
In the second part of the talk, we study (local) Gibbs measures for focusing nonlinear Schrödinger equations. These measures have to be localized by a truncation in the mass in one dimension and in the Wick-ordered (renormalized) mass in dimensions two and three. We show that local Gibbs measures correspond to suitably localized KMS states. This is joint work with Andrew Rout (University of Rennes) and Zied Ammari (University of Besançon, Bourgogne-Franche-Comté).
After a broad introduction to large-time dynamics, the talk will focus on a part of the frontiers of our current understanding of nonlinear stability of traveling waves of partial differential equations, especially on how spectral stability implies nonlinear stability and which kind of dynamics may be expected. We shall highlight main expected difficulties related to the stability of discontinuous and/or characteristic waves of hyperbolic systems, and show a few significant steps obtained by the speaker with respectively Vincent Duchêne (Rennes), Gregory Faye (Toulouse) and Louis Garénaux (Karslruhe).
After a broad introduction to large-time dynamics, the talk will focus on a part of the frontiers of our current understanding of nonlinear stability of traveling waves of partial differential equations, especially on how spectral stability implies nonlinear stability and which kind of dynamics may be expected. We shall highlight main expected difficulties related to the stability of discontinuous and/or characteristic waves of hyperbolic systems, and show a few significant steps obtained by the speaker with respectively Vincent Duchêne (Rennes), Gregory Faye (Toulouse) and Louis Garénaux (Karslruhe).
This talk will focus on the existence of local and global in time weak
martingale solutions for a stochastic version of the Othmer-Dunbar-Alt
kinetic model of chemotaxis under suitable assumptions on the turning
kernel and stochastic drift coefficients, using dispersion and
stochastic Strichartz estimates. The analysis is based on new Strichartz
estimates for stochastic kinetic transport. The derivation of these
estimates involves a local in time dispersion analysis using properties
of stochastic flows, and a time-splitting argument to extend the local
in time results to arbitrary time intervals.
This is based on joint work with Benjamin Gess and Sebastian Herr.
This talk will focus on well-known examples of wave equations, primarily, the classical nonlinear wave equation with a focusing power nonlinearity and the wave maps equation. Both equations exhibit rich dynamics, in particular self-similar blow up solutions. I will report on results concerning the stability of such solutions in the energy supercritical regime and highlight the underlying spectral structures which one needs to understand in order to prove such results. The main focus will lie on results in optimal topologies in terms of L²-based Sobolev spaces, which in turn require the derivation of Strichartz estimates for wave equations with self-similar potentials. This is based on joint work with Roland Donninger.
The controllability problem for a given partial differential equation (PDE) consists in sending any initial condition to zero with a right-hand-side active only in a given subregion ω. It is tightly connected to non-concentration properties for solutions of the said PDE: if no solution can concentrate outside of ω, then controllability from ω holds, and vice versa. The talk will cover two examples of such phenomena.
First, I will explain how controllability of the heat equation is implied by so-called spectral estimates for frequency-localized functions. These spectral estimates are themselves equivalent to an equidistribution property of ω. I will give many examples, including some original results on non-compact manifolds, and a brief idea of the proof. The tools involved draw from spectral theory, harmonic analysis, spectral theory and geometric analysis.
I will then talk about a similar problem for the damped wave equation. In that case, concentration of waves along geodesics of the manifold must be avoided to achieve controllability. When the damping is continuous, the Geometric Control Condition (GCC) gives a sharp condition on the control set: the damping must capture every geodesic in some finite time. I will present some generalizations of the GCC by Burq-Gérard and myself for discontinuous dampings on tori. This talk concerns supercritical wave maps from Minkowski space into slightly perturbed versions of the perfectly round d-sphere. In a work by Shatah and Tahvildar-Zadeh the existence of self-similar blowup solutions to the wave maps equation has already been established in this setting. However, since these solutions were obtained via variational methods proving any form of stability for these solutions has remained out of reach.
Based on a joint work with R. Donninger and B. Schörkhuber I will present a construction of self-similar blowup solutions in the above described setting which are somehow close to the ground-state self-similar solution for the unperturbed sphere. This proximity allowed us to rigorously prove, using perturbative methods, their asymptotic nonlinear stability. We consider particles interacting with a smooth mean-field potential and attempt to quantify the speed of convergence (log-Sobolev constant) of the associated Langevin dynamics in terms of the number N of particles and the strength of the interaction. Our main interest is in relating the scaling of the log-Sobolev constant as a function of N, to properties of the free energy of the model.
We show that a certain notion of convexity of the free energy implies uniform-in-N bounds on the log-Sobolev constant. In some cases, this convexity criterion is sharp — for instance, in the Curie–Weiss model where we prove uniform bounds on the log-Sobolev constant up to the critical temperature, which is optimal.
Our proof does not involve the dynamics. Instead, we decompose the measure describing interactions between particles with inspiration from renormalisation group arguments for lattice models, adapted here to a lattice-free setting in the simplest case of mean-field interactions. Our results apply more generally to non mean-field, possibly random settings, provided each particle interacts with sufficiently many others.
Based on joint work with Roland Bauerschmidt and Thierry Bodineau. We review a method to obtain optimal Poincaré-Hardy inequalities on the hyperbolic spaces. Then we show how to transfer the basic idea to the discrete setting. This yields optimal Poincaré-Hardy-type inequalities on weakly spherically symmetric graphs which include fast enough growing trees and anti-trees. Moreover, this method yields optimal weights which are larger at infinity than the optimal weights constructed via the Fitzsimmons ratio of the square root of the minimal positive Green's function. Joint work with Christian Rose. Exciting topics among the dynamics of nonlinear evolution equations are the occurrence and stability of finite time blowup solutions. In fact, the wave maps equation, Yang–Mills equation, and focusing semilinear wave equation all admit self-similar blowup solutions in closed form. In this talk, I will present a comprehensive stability theory for self-similar blowup solutions of these nonlinear wave equations, which was obtained recently in my PhD thesis. The underlying analysis is based on coordinate systems that are adapted to self-similarity and compatible with the wave evolution. This allows the study of the wave flow near self-similar blowup solutions in spacetime regions that reach from the backward light cone towards the future light cone of the respective singularity. A seminal result of Jordan, Kinderlehrer and Otto states that Fokker–Planck equations on Euclidean spaces can be interpreted as a gradient flow of the relative entropy through optimal transport. In the first part of the talk, I will briefly recall this theory in the usual setting and highlight some iconic generalisations and their consequences. In the second part, based on a joint work with Thomas Leblé, I will present some of the ideas we used to generalise this result to the setting of interacting spin systems, where the underlying space is a countable product of compact Riemannian manifolds, and the range of the interaction is potentially infinite. In particular, I will define the free energy, and the infinite-volume diffusion, partial differential equation and gradient flow that model this situation and show they are related through an Evolution Variational Inequality. Our approach establishes in particular that at high enough temperature the free energy decays exponentially fast along the dynamic, which is new.Singular waves of hyperbolic systems, a frontier in nonlinear wave stability
Abstract
Existence of martingale solutions to a stochastic
kinetic model of chemotaxis
Abstract
On blowup stability in energy supercritical wave equations
Abstract
Controllability Conditions and Non-Concentration Phenomena for the Heat and Wave Equations
Abstract
Stable Blowup for Supercritical Wave Maps into Perturbed Spheres
Abstract
Log-Sobolev Inequality for Mean-Field Particle Systems
Abstract
Optimal Poincaré-Hardy Inequalities on Graphs
Abstract
On Stable Self-Similar Blowup for Nonlinear Wave Equations Beyond Light Cones
Abstract
Gradient Flow of the Free Energy of Infinite Volume Interacting Spin System
Abstract