Gruppen und Symmetrien: Vorlesung 21 ff.¶

Wiederholung: Der Abzählsatz von Pólya¶

Beispiel: Kette mit fünf Perlen¶

Auf wie viele bis auf Drehungen verschiedene Möglichkeiten lässt sich eine $5$-perlige Kette mit den Farben Rot und Blau einfärben, sodass genau $2$ rote und mindestens $1$ blaue Perle auftauchen? Jede Perle soll hierbei entweder rot, blau oder aber gar nicht gefärbt werden. Zur Beantwortung solcher und ähnlicher Fragen wurde Pólyas Abzählsatz besprochen, der sich in folgender algorithmischen Weise anwenden lässt:

Schritt: Bestimmung der Menge $X$ und der auf ihr operierenden Gruppe $G$.
- Hier ist $X = \{1,2,3,4,5\}$ die Menge der $5$ Perlen und $G = \langle \sigma \rangle$ die Gruppe der $5$ Drehungen erzeugt von $\sigma = (1,2,3,4,5)$
Schritt: Bestimmung des Zyklentyps aller Elemente von $G$.
- Hier ist $\sigma^0 = (1)(2)(3)(4)(5)$, $\sigma^1 = (1,2,3,4,5)$, $\sigma^2 = (1,3,5,2,4)$, $\sigma^3 = (1,4,2,5,3)$, $\sigma^4 = (1,5,4,3,2)$.
Schritt: Bestimmung des Zyklenzeigers $Z_G$.
- Hier ist $Z_G(s_1,s_2,s_3,s_4,s_5) = \frac{1}{5}(s_1^5 + 4 s_5)$ (die $4$ $5$-Zykel $\sigma^1,\sigma^2,\sigma^3,\sigma^4$ tragen den Summanden $4 s_5$ und $\sigma^0$ den Summanden $s_1^5$ bei).
Schritt: Aufstellen der Gewichtsfunktion $w$.
- Hier wähle etwa für Rot Gewicht $R$ und für Blau Gewicht $B$ und erhalte $w(R,B) = 1 \cdot R + 1 \cdot B + 1 \cdot 1 = R + B + 1$ (beispielsweise taucht $1 \cdot R$ als Summand auf, weil es genau eine Farbe mit Gewicht $R$ gibt, und der Summand $1 \cdot 1$ bedeutet, dass ungefärbte Perlen mit Gewicht $1$ berücksichtigt werden).
Schritt: Einsetzen der Gewichtsfunktion in den Zyklenzeiger.
- Hier ergibt sich mit einer längeren Rechnung: $$ \begin{align*} & Z_G(w(R,B),w(R^2,B^2),w(R^3,B^3),w(R^4,B^4),w(R^5,B^5)) \\ =& \frac{1}{5} (w(R,B)^5 + 4 w(R^5,B^5)) \\ =& \frac{1}{5} ((R+B+1)^5 + 4 (R^5+B^5+1)) \\ =& R^5 \\ +& R^4 (B+1) \\ +& R^3 (2 B^2 + 4 B + 2) \\ +& R^2 (2 B^3 + 6 B^2 + 6 B + 2) \\ +& R^1 (B^4 + 4 B^3 + 6 B^2 + 4 B + 1) \\ +& R^0 (B^5 + B^4 + 2 B^3 + 2 B^2 + B + 1) \end{align*} $$
Schritt: Ablesen und Aufsummieren der relevanten Koeffizienten.
- Hier sind die Koeffizienten von $R^r B^b$ mit $r = 2$ und $b \geq 1$ relevant, also die von $R^2 B^3$, $R^2 B^2$, $R^2 B$. Ihre Summe ist $2 + 6 + 6 = 14$.

Folglich gibt es bis auf Drehung $14$ solche Ketten mit genau $2$ roten und zumindest $1$ blauen Perle.

Allgemeine Formulierung¶

Gegeben sei die Menge $X = \{1,\ldots,n\}$ und eine Untergruppe $G$ der symmetrischen Gruppe $S_n$.

Außerdem sei $F$ eine endliche Menge von Farben und $$ F \xrightarrow{\:\:w\:\:} \mathbb{N}_0^r $$ eine Gewichtsfunktion. Definiere dann ein Polynom $$ w(X_1,\ldots,X_r) \,:=\, \sum_{k_1,\ldots,k_r} w_{k_1,\ldots,k_r} X_1^{k_1} \cdots X_r^{k_r} $$ mit Koeffizienten $w_{k_1,\ldots,k_r} := |w^{-1}(k_1,\ldots,k_r)|$ der Anzahl Farben vom Gewicht $X_1^{k_1} \cdots X_r^{k_r}$.

Bemerkung. Im Beispiel oben war $r = 2$ und $(X_1,X_2) = (R,B)$.

Die Funktion $w$ induziert eine Gewichtsfunktion $$ G \,\backslash \operatorname{Abb}(X,F) \xrightarrow{\:\:\overline{w}\:\:} \mathbb{N}_0^r $$ auf der Menge der Bahnen mit der Eigenschaft $$ \overline{w}(G f) \,=\, \sum_{i=1}^n w(f(i)) \,. $$ Definiere ein weiteres Polynom $$ \overline{w}(X_1,\ldots,X_r) \,:=\, \sum_{k_1,\ldots,k_r} \overline{w}_{k_1,\ldots,k_r} X_1^{k_1} \cdots X_r^{k_r} $$ mit Koeffizienten $\overline{w}_{k_1,\ldots,k_r} := |\overline{w}^{-1}(k_1,\ldots,k_r)|$ der Anzahl Bahnen vom Gewicht $X_1^{k_1} \cdots X_r^{k_r}$.

Satz (Pólya). Es gilt die folgende Gleichheit von Polynomen: $$ \overline{w}(X_1,\ldots,X_r) \,=\, Z_G(w(X_1,\ldots,X_r),w(X_1^2,\ldots,X_r^2),\ldots,w(X_1^n,\ldots,X_r^n)) $$

Die Platonischen Körper¶

	Feuer	Erde	Luft	Wasser	Kosmos

Klassifikation der regulären Polyeder¶

Reguläre Polyeder sind aus regelmäßigen, zueinander kongruenten Vielecken zusammengesetzt, wobei an jeder Ecke gleich viele Flächen und gleich viele Kanten aufeinandertreffen. Gruppentheoretisch lässt sich Regularität durch folgende Symmetrieeigenschaft charakterisieren:

Für jedes Tripel $(F,K,E)$ bestehend aus einer Fläche $F$ des Polyeders, welche die Kante $K$ mit Endeckpunkt $E$ enthält, und für jedes andere solche Tripel $(F',K',E')$ gibt es eine Symmetrie des dreidimensionalen Raums, die $(F,K,E)$ auf $(F',K',E')$ abbildet.

Satz. Bis auf Größe, Verschiebung und Drehung gibt es genau fünf reguläre Polyeder: die platonischen Körper.

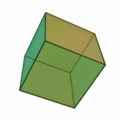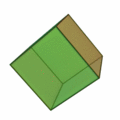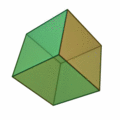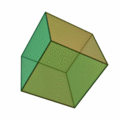
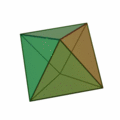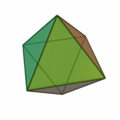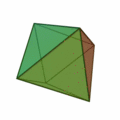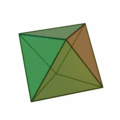
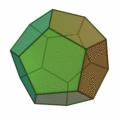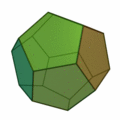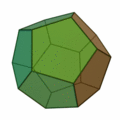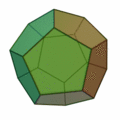
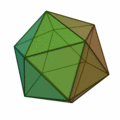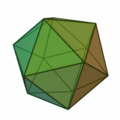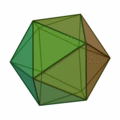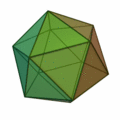
von Wikipedia: Die platonischen Körper	Tetraeder	Hexaeder (Würfel)	Oktaeder	Dodekaeder	Ikosaeder

Art der Seitenflächen	gleichseitige Dreiecke	Quadrate	gleichseitige Dreiecke	regelmäßige Fünfecke	gleichseitige Dreiecke
Anzahl Seitenflächen eines Körpers	4	6	8	12	20
Anzahl Ecken eines Körpers	4	8	6	20	12
Anzahl Kanten eines Körpers	6	12	12	30	30
Anzahl Kanten in einer Körperecke	3	3	4	3	5
dual zu	Tetraeder	Oktaeder	Hexaeder (Würfel)	Ikosaeder	Dodekaeder
Schläfli-Symbol	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}

Beweis des Satzes. Sei $P$ ein reguläres Polyeder, das aus $n$-Ecken $F$ zusammengesetzt ist, sodass an jeder Ecke $E$ genau $m$ Flächen aufeinandertreffen. Da die Winkel zwischen benachbarten Kanten in den regulären $n$-Ecken $F$ alle gleich $\pi - \frac{2 \pi}{n}$ sind, muss gelten: $$ m \left( \pi - \frac{2 \pi}{n} \right) < 2 \pi $$ Diese Ungleichung lässt sich umstellen zu $$ \frac{1}{2} < \frac{1}{n} + \frac{1}{m} \,. $$ Es gilt natürlich $n,m \geq 3$. Wegen der Ungleichung muss deshalb $n,m \leq 5$ sein. Durchprobieren aller Möglichkeiten $n, m \in \{3,4,5\}$ liefert folgende Lösungspaare für die Ungleichung: $$ (n,m) \in \{ (3,3), (4,3), (3,4), (5,3), (3,5) \} $$ Ein Vergleich mit (dem Schläfli-Symbol in) obiger Tabelle zeigt, dass $P$ ein platonischer Köper sein muss.

$ \square $

Bemerkung. Streng genommen müsste für einen vollständigen Beweis noch gezeigt werden, dass die platonischen Körper auch tatsächlich existieren.

Symmetriegruppen der platonischen Körper¶

Dualität¶

Das duale Polyeder $P'$ eines Polyeders $P$ ergibt sich, indem die Flächenmittelpunkte von $P$ als Ecken von $P'$ gewählt und zwei Ecken von $P'$ durch eine Kante verbunden werden, wenn die zugehörigen Flächen in $P$ eine gemeinsame Kante haben. Zweimaliges Anwenden dieser Konstruktion liefert wieder ein Polyeder "gleichen Typs" wie $P$, d.h. bis auf Größe, Drehung und Verschiebung gilt $P'' = P$.

Jeder platonische Körper besizt in diesem Sinne einen zugehörigen dualen platonischen Körper:

Das Tetraeder ist selbstdual:
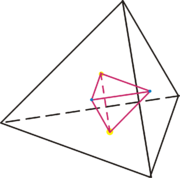
Das Oktaeder ist dual zum Hexaeder (Würfel).
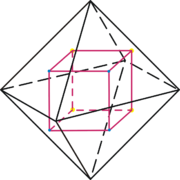
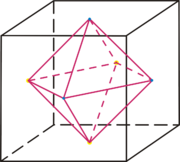
Das Ikosaeder ist dual zum Dodekaeder.

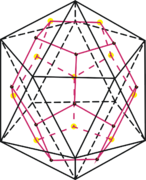
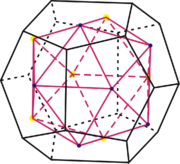
Duale platonische Körper haben dieselben räumlichen Symmetrien, sodass zur Bestimmung der Symmetriegruppen aler platonischen Körper nur diejenigen von Tetraeder, Würfel und Dodekaeder ermittelt werden müssen.

Symmetrien des Tetraeders¶

Bezeichne mit $A,B,C,D$ die Ecken des Tetraeders (siehe Abbildung unten). Die Gruppe $G$ aller räumlichen Symmetrien erzeugt von den Drehungen, die das Tetraeder auf sich selbst abbilden, operiert auf der Menge $$ X \,=\, \{ABD,BCD,CAD,ABC\} \,{\hat =}\, \{1,2,3,4\} $$ der Flächen des Tetraeders. Dies liefert einen Gruppenhomomorphismus $G \to S_4$. Er ist injektiv, weil jede Symmetrie vollständig durch ihre Wirkung auf die Flächen beschrieben wird. Auf diese Weise lässt sich $G$ als Untergruppe von $S_4$ auffassen, die aus folgenden Elementen besteht:

Insgesamt $4 \times 2 = 8$ Drehungen von $\pm 120^\circ$ um eine Achse durch eine Ecke und den gegenüberliegenden Flächenmittelpunkt.

Zum Beispiel $(1,2,3) \in S_4$:
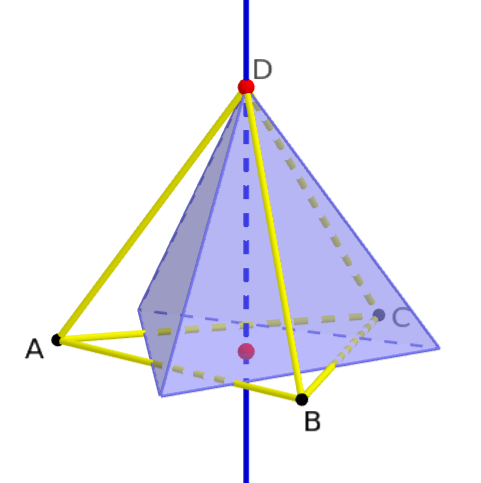
Insgesamt $\frac{6}{2} = 3$ Drehungen von $180^\circ$ um eine Achse durch zwei sich gegenüberliegende Kantenmittelpunkte.

Zum Beispiel $(1,4) \circ (2,3) \in S_4$:

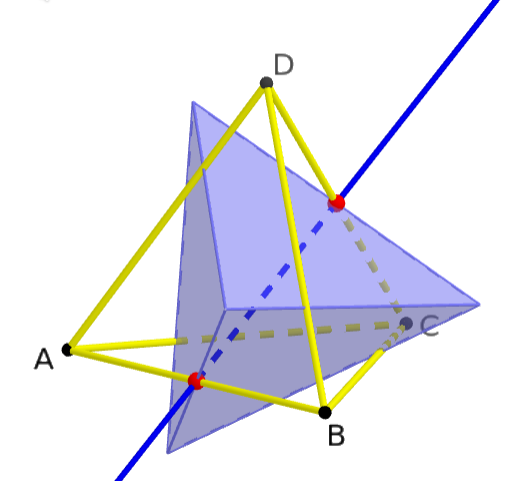
Zusammen mit der Identität $() \in S_4$ enthält $G$ damit $12$ Elemente. Explizit ist $$ G \,=\, \{ (), (1,2,3), (1,3,2), (1,2,4), (1,4,2), (1,3,4), (1,4,3), (2,3,4), (2,4,3), (1,2) \circ (3,4), (1,3) \circ (2,4), (1,4) \circ (2,3) \} \,. $$ und der Zyklenzeiger berechnet sich somit als $$ Z_G(s_1,s_2,s_3,s_4) \,=\, \frac{1}{12} (s_1^4 + 3 s_2^2 + 8 s_1 s_3) \,. $$

Das Vorzeichen aller Elemente von $G$ ist positiv (d.h. $\operatorname{sgn}(\sigma) = 1$ für alle $\sigma \in G$). Somit gilt $G \subseteq A_4$. Wegen $|G| = 12 = \frac{4!}{2} = |A_4|$ ist die Symmetriegruppe $G$ des Tetraeders demzufolge die alternierende Gruppe $$ G \,=\, A_4 \,. $$

Bemerkung. Die volle Symmetriegruppe $H$ des Tetraeders, deren Erzeuger neben den Drehungen auch die räumlichen Spiegelungen sind, die das Tetraeder auf sich selbst abbilden, ist die symmetrische Gruppe $S_4$. In der Tat zeigt die obige Argumentation ja $G \leq H \leq S_4$. Wegen $H \neq G$ und $[S_4 : G] = 2$ muss daher $H = S_4$ gelten.

Beispiel eines Färbungsproblems. Die Anzahl der bis auf Drehung verschiedenen Möglichkeiten, die Tetraederflächen mit $n$ Farben einzufärben, ist $$ Z_G(n,n,n,n) = \frac{1}{12}(n^4 + 11 n^2) \,. $$ Für $n = 2$ Farben ergeben sich also beispielsweise $\frac{16 + 44}{12} = 5$ Färbungen.

Symmetrien von Hexaeder (Würfel) und Oktaeder¶

Bezeichne mit $A,B,C,D,E,F,G,H$ die Würfelecken (siehe unten). Wie beim Tetraeder operiert die Gruppe $G$ aller räumlichen Symmetrien erzeugt von den Drehungen, die den Würfel auf sich selbst abbilden, auf der Menge $$ X \,=\, \{ADEF,BAFG,CBGH,DCHE,ABCD,EHGF\} \,{\hat =}\, \{1,2,3,4,5,6\} $$ der sechs Würfelflächen, womit sich $G$ als Untergruppe von $S_6$ auffassen lässt, die aus folgenden Elementen besteht:

Insgesamt $\frac{6}{2} \times 2 = 6$ Drehungen von $\pm 90^\circ$ um eine Achse durch zwei sich gegenüberliegende Flächenmittelpunkte.

Zum Beispiel $(1,2,3,4) \in S_6$:
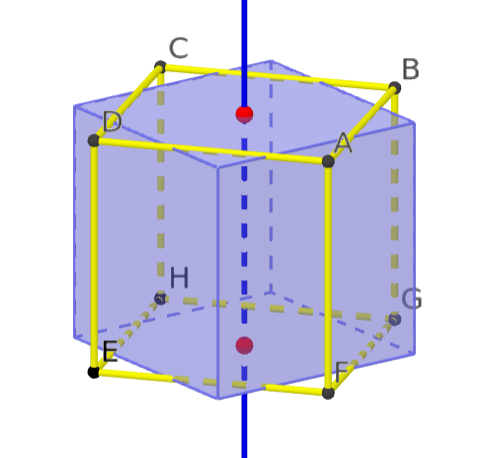
Insgesamt $\frac{6}{2} = 3$ Drehungen von $180^\circ$ um eine Achse durch zwei sich gegenüberliegende Flächenmittelpunkte.

Zum Beispiel $(1,2,3,4)^2 = (1,3) \circ (2,4) \in S_6$.
Insgesamt $\frac{8}{2} \times 2 = 8$ Drehungen von $\pm 120^\circ$ um eine Achse durch zwei sich gegenüberliegende Ecken.

Zum Beispiel $(1,6,4) \circ (2,3,5) \in S_6$:
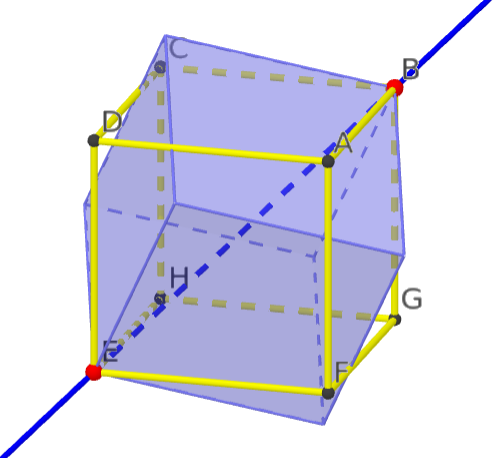
Insgesamt $\frac{12}{2} = 6$ Drehungen von $180^\circ$ um eine Achse durch zwei sich gegenüberliegende Kantenmittelpunkte.

Zum Beispiel $(1,6) \circ (2,4) \circ (3,5) \in S_6$:

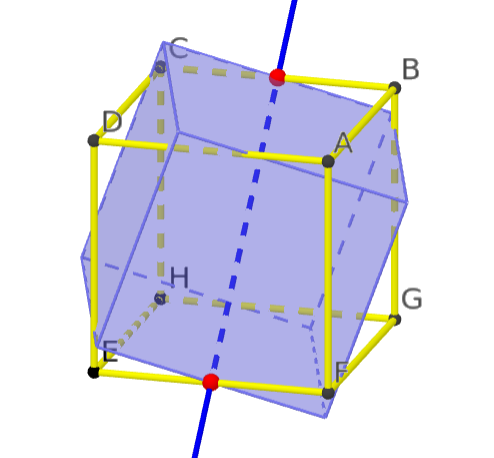
Zusammen mit der Identität $() \in S_6$ enthält $G$ damit $24$ Elemente und der Zyklenzeiger ist $$ Z_G(s_1,s_2,s_3,s_4,s_5,s_6) \,=\, \frac{1}{24} (s_1^6 + 6 s_2^3 + 8 s_3^2 + 6 s_1^2 s_4 + 3 s_1^2 s_2^2) \,. $$

Bemerkung. Die Operation von $G$ auf den vier Diagonalen des Würfels entspricht einem injektiven Gruppenhomomorphismus $G \to S_4$. Wegen $|G| = 24 = 4! = |S_4|$ ergibt sich für die Symmetriegruppe des Würfels also $$ G \,\cong\, S_4 \,. $$

Die volle Symmetriegruppe $H$ des Würfels ist erzeugt von den Drehungen in $G$ und den räumlichen Spiegelungen, die den Würfel auf sich selbst abbilden. Diese Spiegelungen lassen sich alle aus der Spiegelung $(5,6) \in S_6$, die Ober- und Unterseite des Würfels tauscht, durch Konjugation mit Drehungen aus $G$ erhalten. Hieraus schließlich folgt $$ H \,\cong\, S_4 \times \mathbb{Z}/2\mathbb{Z} \,. $$

Beispiel eines Färbungsproblems. Die Anzahl der bis auf Drehung verschiedenen Färbungen der Würfelflächen mit $n$ Farben ist $$ Z_G(n,n,n,n,n,n) = \frac{1}{24}(n^6 + 3 n^4 + 12 n^3 + 8 n^2) \,. $$ Für $n = 3$ Farben ergeben sich also beispielsweise $\frac{3^6 + 3 \cdot 3^4 + 12 \cdot 3^3 + 8 \cdot 3^2}{24} = 57$ Färbungen.

Symmetrien von Dodekaeder und Ikosaeder¶

Die Gruppe $G$ aller räumlichen Symmetrien erzeugt von den Drehungen, die das Dodeakeder auf sich selbst abbilden, operiert auf der Menge $$ X \,{\hat =}\, \{1,2,3,\ldots,12\} $$ der zwölf Flächen des Dodekaeders, womit sich $G$ als Untergruppe von $S_{12}$ auffassen lässt. Hier sei angenommen, dass $11$ "die obere" Fläche und $12$ "die untere" bezeichnet und außerdem die übrigen Flächen auf der "oberen Ebene" mit $1,2,3,4,5$ und die auf der "unteren Ebene" mit $6,7,8,9,10$ gegen den Uhrzeigersinn durchnummeriert sind, sodass $1$ die Fläche "direkt über" $6$ und $7$ benennt. Die Elemente von $G$ sind dann die folgenden:

Insgesamt $\frac{12}{2} \times 4 = 24$ Drehungen von $\pm 72^\circ$ und $\pm 144^\circ$ um eine Achse durch zwei sich gegenüberliegende Flächenmittelpunkte.

Zum Beispiel $(1,2,3,4,5) \circ (6,7,8,9,10) \in S_{12}$:
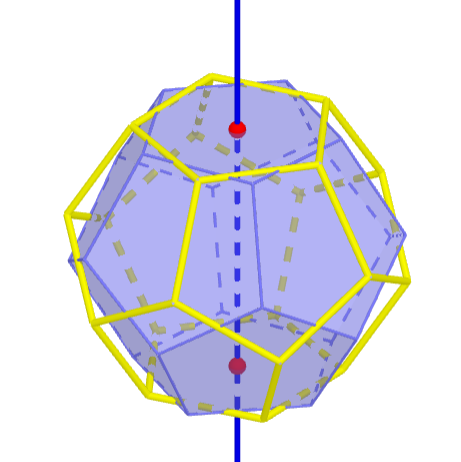
Insgesamt $\frac{20}{2} \times 2 = 20$ Drehungen von $\pm 120^\circ$ um eine Achse durch zwei sich gegenüberliegende Ecken.

Zum Beispiel $(1,8,4) \circ (2,3,11) \circ (5,7,9) \circ (6,12,10) \in S_{12}$:
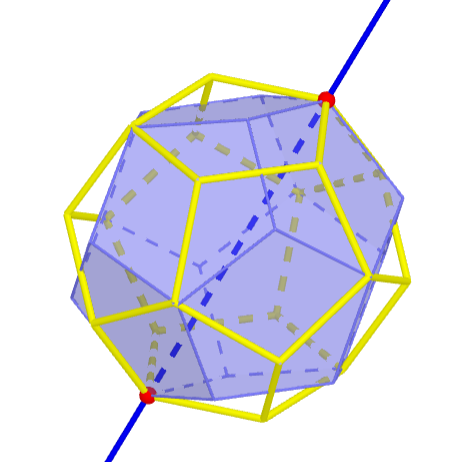
Insgesamt $\frac{30}{2} = 15$ Drehungen von $180^\circ$ um eine Achse durch zwei sich gegenüberliegende Kantenmittelpunkte.

Zum Beispiel $(1,9) \circ (2,4) \circ (3,11) \circ (5,8) \circ (6,12) \circ (7,10) \in S_{12}$:

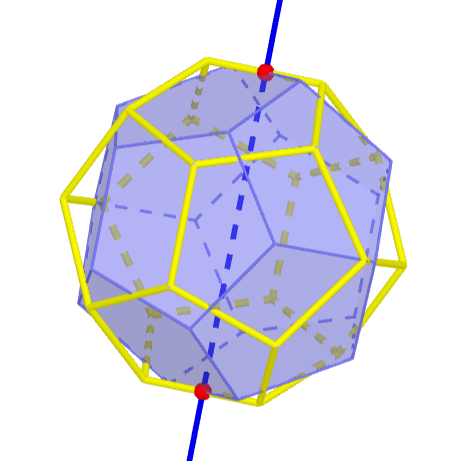
Zusammen mit der Identität $() \in S_{12}$ enthält $G$ damit $60$ Elemente und der Zyklenzeiger ist $$ Z_G(s_1,s_2,s_3,\ldots,s_{12}) \,=\, \frac{1}{60} (s_1^{12} + 15 s_2^6 + 20 s_3^4 + 24 s_1^2 s_5^2) \,. $$

Bemerkung. Es gibt fünf Möglichkeiten acht Ecken des Dodekaeders zu wählen, sodass diese die Eckpunkte eines eingeschriebenen Würfels bilden:

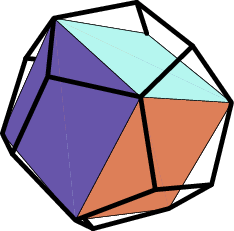
Die Operation von $G$ auf der Menge dieser fünf Würfel liefert einen injektiven Gruppenhomomorphismus $G \to S_5$ und es folgt für die Symmetriegruppe des Dodekaeders wegen $|G| = 60 = \frac{5!}{2} = |A_5|$ die Isomorphie $$ G \,\cong\, A_5 \,. $$

Mit einer ähnlichen Begründung wie oben im Fall des Würfels gegeben berechnet sich die volle Symmetriegruppe $H$ des Dodekaeders, welche neben den Drehungen in $G$ noch von den räumlichen Spiegelungen erzeugt wird, die das Dodekaeder auf sich selbst abbilden, damit als $$ H \,\cong\, A_5 \times \mathbb{Z}/2\mathbb{Z} \,. $$

Beispiel eines Färbungsproblems. Die Anzahl der bis auf Drehung verschiedenen Färbungen der Dodekaederflächen mit $n$ Farben ist $$ Z_G(n,n,n,\ldots,n) = \frac{1}{60}(n^{12} + 15 n^6 + 44 n^4) \,. $$ Für $n = 5$ Farben ergeben sich also beispielsweise $\frac{5^{12} + 15 \cdot 5^6 + 44 \cdot 5^4}{60} = 4073375$ Färbungen.

Klassifikation der endlichen Drehgruppen¶

Der folgende Satz ist interessant, weil er zeigt, dass jede endliche Gruppe, die aus Drehungen des Raums besteht, entweder die Symmetriegruppe eines platonischen Körpers ist oder aber eine der in dieser Vorlesung schon oft beispielhaft betrachteten Gruppen $\mathbb{Z} / n \mathbb{Z}$ und $D_n$.

Satz. Jede endliche Gruppe $G$ von Drehungen des dreidimensionalen euklidischen Raums ist eine der folgenden Gruppen:

Eine zyklische Gruppe $C_n$ mit $n \geq 1$, die aus den $n$ Drehungen um eine fixierte Achse mit Winkeln $2 \pi k / n$ für $k \in \{0,1,2,\ldots,n-1\}$ besteht.
Eine Diedergruppe $D_2$, die aus den vier Drehungen besteht, welche zwei fixierte orthogonale Geraden jede in sich selbst überführen.
Eine Diedergruppe $D_n$ mit $n > 2$, die aus den $2n$ räumlichen Drehsymmetrien eines fixierten in einer Ebene liegenden regelmäßigen $n$-Ecks besteht. (Eine Spiegelung im zweidimensionalen kann im dreidimensionalen Raum als Drehung realisiert werden!)
Eine Symmetriegruppe eines platonischen Körpers.

Beweis (aus einem Skript von Wolfgang Sörgel).

Für jedes vom neutralen Element verschiedene Element $g \in G \setminus \{1\}$ unserer Gruppe definieren wir seine "Pole" als die beiden Schnittpunkte seiner Drehachse mit der Einheitssphäre. Sei $P$ die Menge aller Pole von Elementen aus $G \setminus \{1\}$. Natürlich ist $P$ eine endliche Menge und $G$ operiert auf $P$.

Wir zählen nun die Menge $M$ aller Paare $(g, p)$ mit $g \in G \setminus \{1\}$ und $p$ einem Pol von $g$ auf zwei Weisen: Einmal gehört jedes von $1$ verschiedene Gruppenelement $g \in G \setminus \{1\}$ zu genau zwei Polen, also haben wir $$ |M| \,=\, 2 (|G| - 1) \,. $$ Andererseits gehört jeder Pol $p \in P$ zu genau $|G_p| - 1$ von $1$ verschiedenen Gruppenelementen, also haben wir $$ |M| \,=\, \sum_{p \in P} (|G_p| - 1) \,. $$ Zusammen erhalten wir so die Gleichung $$ 2 (|G| - 1) \,=\, \sum_{p \in P} (|G_p| - 1) \,. $$ Sei nun $P = P_1 \cup \cdots \cup P_r$ die Bahnzerlegung von $P$ und seien $p_i \in P_i$ fest gewählt. Der Stabilisator $G_{p_i}$ von $p_i$ habe sagen wir $n_i \geq 2$ Elemente. Die zugehörige Bahn hat dann $|P_i| = |G|/n_i$ Elemente, und alle Stabilisatoren zu Polen aus $P_i$ haben auch $n_i$ Elemente. Fassen wir also die Pole jeder Bahn in unserer Summe zu einem Summanden zusammen, so können wir in unserer Gleichung die rechte Seite umformen zu $$ \sum_{i=1}^r (|G|/n_i) (n_i - 1) $$ und es ergibt sich die Gleichung $$ 2 - \frac{2}{|G|} \,=\, \sum_{i=1}^r \left(1 - \frac{1}{n_i}\right) \,. $$ Jeder Summand auf der rechten Seite ist mindestens $\frac{1}{2}$, der Ausdruck links ist aber kleiner als $2$. Es kommen also nur bis zu drei Bahnen von Polen in Betracht. Wir machen nun eine Fallunterscheidung nach der Zahl $r$ der Bahnen von Polen.

Fall 0. Es gibt überhaupt keine Pole. In diesem Fall besteht $G$ nur aus dem neutralen Element, und wir haben die Gruppe $C_1$ vor uns.

Fall 1. Ganz $P$ ist eine Bahn. Das ist unmöglich, denn es muss $|G| \geq 2$ gelten, wenn es überhaupt Pole geben soll, und damit hätten wir $$ 2 - \frac{2}{|G|} \,\geq\, 1 \,>\, 1 - \frac{1}{n_1} $$ im Widerspruch zu unserer Gleichung.

Fall 2. Es gibt genau zwei Bahnen $P_1$ und $P_2$ in P. Wir haben dann $$ \frac{2}{|G|} \,=\, \frac{1}{n_1} + \frac{1}{n_2} \,. $$ Da $n_1$ und $n_2$ Teiler sind von $|G|$, haben wir $n_i \leq |G|$ und damit notwendig $n_1 = n_2 = |G|$. Alle Pole werden also von der Gruppe festgehalten, es gibt folglich nur zwei Pole, die sich notwendig gegenüberliegen müssen. Damit sind wir im Fall der zyklischen Gruppen $C_n$ mit $n > 1$.

Fall 3. Es gibt genau drei Bahnen $P_1$, $P_2$ und $P_3$ in $P$, wir haben also $$ \frac{2}{|G|} \,=\, \frac{1}{n_1} + \frac{1}{n_2} + \frac{1}{n_3} - 1 \,. $$ Wir dürfen annehmen $n_1 \leq n_2 \leq n_3$. Sicher gilt dann $n_1 = 2$, sonst wäre die rechte Seite $\leq 0$. Haben wir auch $n_2 = 2$, so kann $n_3$ beliebige Werte annehmen und wir haben $|G| = 2 n_3$. Die Bahn $P_3$ besteht dann aus zwei Polen, die sich notwendig gegenüberliegen, und die Gruppe wird eine Diedergruppe $D_{n_3}$. Sicher sind $(2,4,4)$ und $(2,3,6)$ unmöglich für $(n_1,n_2,n_3)$, da $\frac{1}{2} + \frac{1}{4} + \frac{1}{4} - 1 = 0 = \frac{1}{2} + \frac{1}{3} + \frac{1}{6}$, also bleiben nur die Fälle $(2, 3, 3)$, $(2, 3, 4)$ und $(2, 3, 5)$, und man berechnet leicht die zugehörigen Gruppenordnungen zu $12$, $24$, und $60$. Die Ecken des zugehörigen Tetraeders bzw. Würfels bzw. Dodekaeders sind nun genau die Elemente von $P_2$, und wir überlassen den Rest des Beweises dem Leser.

$ \square $

Elliptische Kurven¶

Im Folgenden sei $K$ ein Körper, in dem $2$ und $3$ multiplikativ invertierbar sind.

Zulässige Wahlen für $K$ sind also zum Beispiel die reellen Zahlen $K = \mathbb{R}$ oder auch $K = \mathbb{Z} / p \mathbb{Z}$ für Primzahlen $p > 3$.

Definition¶

Eine elliptische Kurve ist eine ebene Kurve gegeben als Lösungsmenge

$$ E \,:=\, E_{a,b} \,:=\, \big\{ (x,y) \in K^2 : y^2 = x^3 + a x + b \big\} \cup \big\{ \infty \big\} $$

für feste Parameter $a, b \in K$ mit der Eigenschaft $\delta_{a,b} := 4 a^3 + 27 b^2 \neq 0$.

Bemerkung. Im Fall $K = \mathbb{R}$ der reellen Zahlen entscheidet das Vorzeichen von $\delta_{a,b}$, ob der Graph der elliptischen Kurve $E_{a,b}$ zusammenhängend ist. Bei positivem Vorzeichen ist dies der Fall und bei negativem besteht er aus zwei Komponenten.

Zum Beispiel besitzt die elliptische Kurve $E_{-1,2}$ den Wert $\delta_{-1,2} = 4 \cdot (-1)^3 + 27 \cdot 2^2 = 104 > 0$ und hat einen zusammenhängenden Graphen:

Für die elliptische Kurve $E_{-2,1}$ hingegen ergibt sich $\delta_{-2,1} = 4 \cdot (-2)^3 + 27 \cdot 1^2 = -5 < 0$ und der Graph besteht aus zwei Komponenten:

Bemerkung. Ist $K$ ein endlicher Körper mit $q$ Elementen, so besteht natürlich auch die Kurve $E$ aus nur endlich vielen Punkten. Die Anzahl $N$ der Punkte auf $E$ genügt dann der sogenannten Hasse-Schranke: $$ |N - (q+1)| \leq 2 \sqrt{q} $$

Gruppenstruktur¶

Auf jeder elliptischen Kurve $E = E_{a,b}$ lässt sich eine Verknüpfung $+$ definieren, unter der $E$ zur abelschen Gruppe wird. Diese Verknüpfung hat einen geometrischen Ursprung und lässt sich explizit folgendermaßen beschreiben:

Zunächst wird für alle Punkte $P$ auf $E$ $$ \begin{align} P + \infty &~:=~ P \\ \infty + P &~:=~ P \end{align} $$ verlangt, wodurch $\infty$ zum neutralen Element von $+$ wird.

Der Spiegelpunkt für von $\infty$ verschiedene Punkte $P = (x_P, y_P)$ auf $E$ ist der Punkt $-P := (x_P, -y_P)$, der sich durch Spiegelung an der $x$-Achse ergibt. Da $y$ quadratisch in der $E$ definierenden Gleichung auftaucht, liegt mit $P$ auch $-P$ auf $E$.

Durch die Forderung $$ P + (-P) \::=\: \infty $$ wird $-P$ zum Inversen von $P$ bezüglich $+$.

Schließlich setze für Punkte $P = (x_P, y_P)$ und $Q = (x_Q, y_Q)$ mit $Q \neq -P$ auf $E$

$$ P + Q \::=\: \left( s_{PQ}^2 - x_P - x_Q, -s_{PQ}^3 + (2 x_P + x_Q) s_{PQ} - y_P \right) \,, $$

wobei der Steigungsparameter $s_{PQ}$ zu berechnen ist als

$$ s_{PQ} \::=\: \begin{cases} \frac{y_P - y_Q}{x_P - x_Q} & \text{falls $x_P \neq x_Q$,} \\ \frac{3 x_P^2 + a}{2 y_P} & \text{falls $x_P = x_Q$.} \end{cases} $$

Bemerkung. Die Verknüpfung $P+Q$ zweier Punkte $P$, $Q$ auf $E$ ist gerade so definiert, dass $-(P+Q)$ der eindeutige dritte Schnittpunkt $R$ von $E$ mit der Geraden durch $P$ und $Q$ ist:

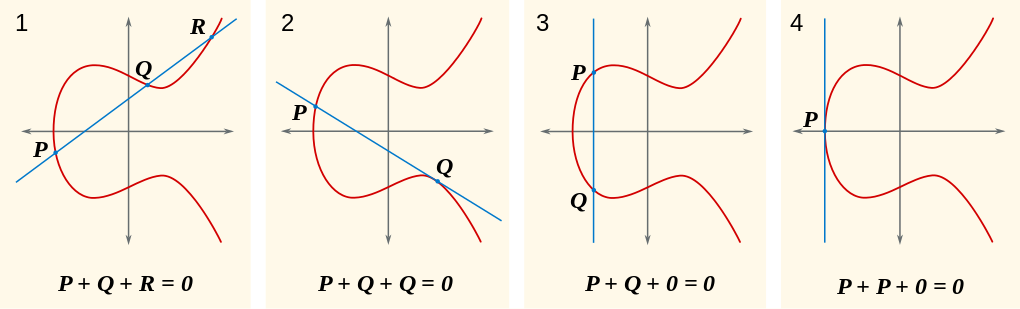
Der Fall 1 zeigt die "generische" Situation, wo die Punkte $P \neq Q$ verschieden sind und die Gerade $PQ$ keine Tangente von $E$ ist. Die Fälle 2-4 sind in dem Sinn "entartet", dass die Gerade $PQ$ Tangente von $E$ in $Q$ ist (Fall 2) bzw. der dritte Schnittpunkt im Unendlichen $\infty$ liegt (Fall 3) bzw. die Punkte $P$ und $Q$ zusammenfallen und die Tangente in diesem Punkt als einzigen weiteren Schnittpunkt mit $E$ den Punkt $\infty$ besitzt (Fall 4).

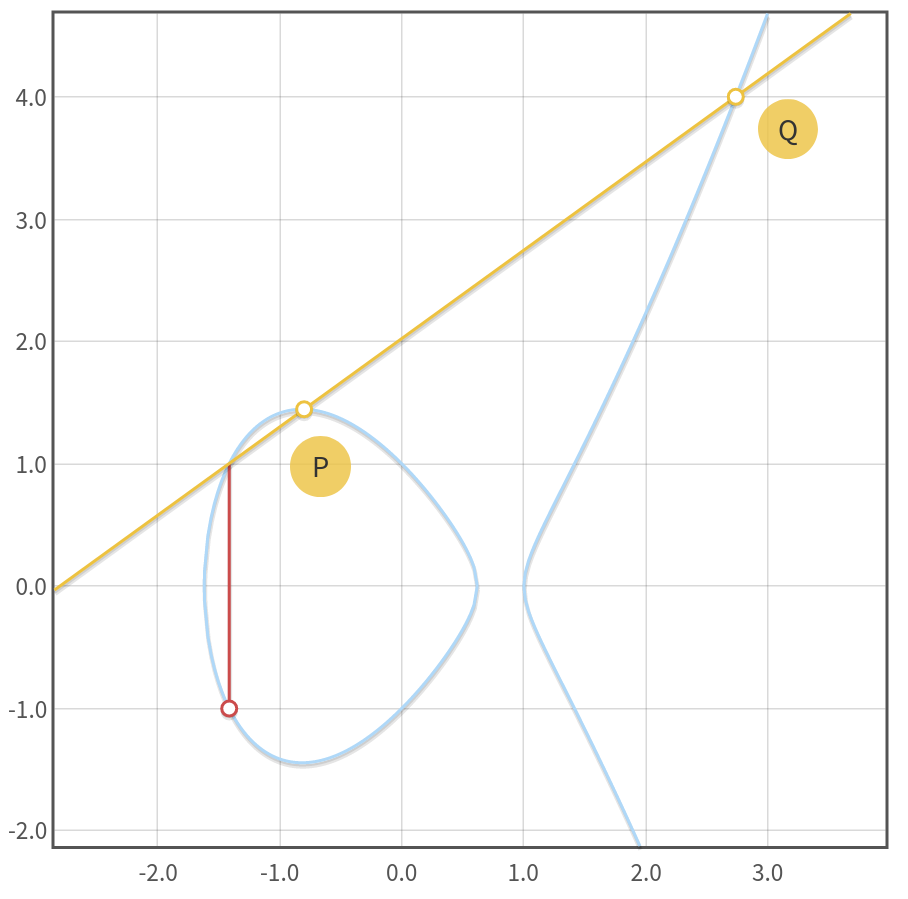
In der generischen Situation funktioniert die Addition zweier Punkte $P, Q$ auf $E$ also wie folgt:

Zeichne die Gerade durch $P$ und $Q$ und bestimme ihren dritten Schnittpunkt $R$ mit $E$.
Spiegle $R$ an der $x$-Achse. Der so erhaltene Punkt ist die Summe $P + Q$.

Folgendes Online-Tool ermöglicht es, die Addition der Punkte interaktiv nachzuvollziehen:

Satz. Mit der Verknüpfung $+$ wird jede elliptische Kurve $E$ zur abelschen Gruppe.

Beweis. Folgende Eigenschaften müssen überprüft werden, worauf hier aber verzichet wird:

Assoziativität: $(P + Q) + R = P + (Q + R)$ für alle Punkte $P, Q, R$ auf $E$.
Kommutativität: $P + Q = Q + P$ für alle Punkte $P, Q$ auf $E$.
Existenz eines neutralen Elements: Das neutrale Element ist $\infty$ wegen $P + \infty = P = \infty + P$ für alle Punkte $P$ auf $E$.
Existenz von inversen Elementen: Das zu einem Punkt $P = (x_P, y_P)$ auf $E$ inverse Element ist $-P$ wegen $P + (-P) = \infty$.

$ \square $

Wiederholung: Diskreter Logarithmus¶

Sei $G$ eine Gruppe. Für ein fixiertes Element $g$ von $G$ der Ordnung $n$ wird die Umkehrabbildung des Gruppenisomorphismus $$ \begin{array}{rcrcl} \exp_g &\colon& \mathbb{Z} / n \mathbb{Z} &\to& \langle g \rangle \\ && \overline{x} &\mapsto& g^x \end{array} $$ als diskreter Logarithmus $\log_g$ bezeichnet.

Diskrete Logarithmen finden Anwendung in der Kryptographie. Hierzu wird eine "hinreichend komplizierte" Gruppe $G$ gewählt, für die das Berechnen der diskreten Logarithmen sehr schwierig aber das Berechnen von Potenzen einfach ist. Das heißt, bei Kenntnis von $g \in G$ und $h \in \langle g \rangle$ darf dasjenige $\overline{x} \in \mathbb{Z} / n \mathbb{Z}$ mit $h = g^x$ nur schwer berechenbar sein, wohingegen für gegebenes $g \in G$ und $x \in \mathbb{Z}$ die Potenz $g^x$ einfach zu berechnen sein muss.

Die Elliptische-Kurven-Kryptographie macht sich die Tatsache zunutze, dass die Gruppenstruktur von geeignet gewählten elliptischen Kurven über endlichen Körpern als in diesem Sinne "hinreichend kompliziert" eingestuft wird.

Beispiel (Diffie-Hellmann-Schlüsselaustausch). Fixiere eine Gruppe $G$ und ein Element $g$ in $G$ der Ordnung $n$.

Ein privater Schlüssel besteht in der Wahl einer Zahl $x \in \mathbb{Z}$ mit $0 < x < n$. Der zugehörige öffentliche Schlüssel ist $h = g^x$.

Wollen zwei Parteien $A$ und $B$ einen geheimen, d.h. nur ihnen beiden bekannten Schlüssel $k$ erstellen, können sie wie folgt vorgehen:

Beide Parteien wählen nur ihnen selbst bekannte, private Schlüssel $x_A$ und $x_B$.
Dann berechnen und veröffentlichen sie jeweils die zugehörigen öffentlichen Schlüssel $h_A$ und $h_B$.
Als geheimer Schlüssel kann nun $k = g^{x_A \cdot x_B}$ dienen.

In der Tat kann $A$ einerseits $k = h_B^{x_A}$ und $B$ andererseits $k = h_A^{x_B}$ allein mit Kenntnis der öffentlichen und des jeweiligen eigenen privaten Schlüssels berechnen. Unter der Annahme, dass diskrete Logarithmen in der Gruppe $G$ schwierig zu berechnen sind, kann der geheime Schlüssel $k$ jedoch von Außenstehenden selbst bei Kenntnis beider öffentlicher Schlüssel $h_A$ und $h_B$ nicht leicht ermittelt werden.

Beispiel (Elgamal-Verschlüsselungsverfahren). Der im Diffie-Hellmann-Schlüsselaustausch erstellte, geheime Schlüssel $k$ lässt sich auch direkt zum Verschlüsseln nutzen. Möchte $A$ nämlich die Nachricht $h \in G$ verschlüsselt an $B$ schicken, funktioniert dies ganz einfach folgendermaßen:

$A$ verschlüsselt die Nachricht als $l = k h$.
$B$ entschlüsselt die Nachricht als $h = k^{-1} l$.

Bemerkung (siehe NIST.FIPS.DSS für Details). Typischerweise werden in kryptographischen Anwendungen elliptische Kurven $E_{a,b}$ über endlichen Körpern $K = \mathbb{Z}/p\mathbb{Z}$ mit einem fixierten Element $g \in E_{a,b}$ der Ordnung $n$ durch ihre sogenannten domain parameter $(p,a,b,g,n,m)$ angegeben, wobei $m$ den Index der Untergruppe $\langle g \rangle$ bezeichnet. In der Praxis verwendet werden Parameter mit folgenden Eigenschaften:

$p$ ist eine Primzahl größer $2^{191} \approx 10^{58}$.
$a = -3$ "for efficiency" und $b$ "pseudo-randomly" gewählt.
$g$ ist ein beliebiger Punkt der Ordnung $n$.
$n$ ist eine Primzahl mit ungefähr gleicher Bit-Länge wie $p$.
$m$ ist möglichst klein.

Üblicherweise gilt für die Bit-Länge $\lceil \log_2(p) \rceil \in \{192,224,256,384,521\}$ und für den Index $m \in \{1,2,4\}$.

Das Security-Level bei solcher Wahl der domain parameter wird aktuell als $\frac{1}{2} \lceil \log_2(p) \rceil$-bit angesetzt. Alle die Sicherheit betreffenden Aussagen sollten aber natürlich stets mit Vorsicht genossen werden, zum Beispiel wegen möglicher Einflussnahme der NSA.