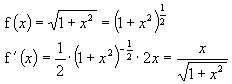Um den Zusammenhang klar zu machen, hier zunächst eine Zeichnung.
Die
Punkte x und x+h können mit der Maus bewegt werden.
Neben dem Mechanismus der Verkettung wird auch gezeigt, wie sich die Sekantensteigungen
an den beiden Funktionen f und g sowie an der verketteten Funktion g![]() f
zueinander verhalten.
f
zueinander verhalten.
Das folgende Bild zeigt den selben Zusammenhang in einer Zeichnung, die mit The Geometer's Sketchpad erstellt wurde. Um mit der Zeichnung zu arbeiten, muß eine Sketchpad-Version (erhältlich für Macintosh oder Windows, auch als Demo) auf eurem Rechner installiert sein. Außerdem muß euer Browser so eingestellt sein, daß er Dateien mit der Endung .gsp mit Sketchpad öffnet. Dann könnt ihr die Zeichnung mit einem Klick auf das Bild laden.
| In der Zeichnung ist |
|
Eingezeichnet sind die Steigungsdreiecke, die sich durch die Wahl der
Punkte x und x+h auf der x-Achse für die drei
Funktionen ergeben.Wir bezeichnen:
dx = (x+h) - x,
dz = f(x+h) - f(x),
dy = g(f(x+h)) - g(f(x)).
An den beiden Hilfskonstruktionen sieht man den Zusammenhang, in dem die Dreiecke stehen. Stellen wir den üblichen Quotienten für die Sekantensteigung auf, so sehen wir, daß für die gesuchte Steigung gilt:
Dieser Bruch läßt sich mit dz erweitern. Es ergibt sich:
Die Sekantensteigung im grünen Dreieck ist das Produkt aus den Sekantensteigungen im blauen und im roten Dreieck.
Wenn h gegen 0 konvergiert, gehen die Sekantensteigungen in die
entsprechenden Tangentensteigungen über: dz/dx nähert
sich der "inneren Ableitung" f'(x), dy/dz der
"äußeren Ableitung"
g'(f(x)) an.
Weil dy/dx sich der gesuchten "gesamten" Ableitung annähert,
müssen wir die beiden Ableitungen oben multiplizieren und erhalten ...
|
Wir wenden nun die Kettenregel auf das Beispiel unserer Zeichnung an:
f(x) = (x-5)2 = x2 - 10x
+ 25 f '(x)
= 2x - 10
g(z) = sin z
g'(z) = cos z
(g![]() f)'(x)
=(g(f(x)))' = g'(f(x))
f)'(x)
=(g(f(x)))' = g'(f(x)) ![]() f '(x) = cos((x-5)2 )
f '(x) = cos((x-5)2 ) ![]() (2x -10)
(2x -10)
[Natürlich läßt sich auch f '(x) bereits mit
der Kettenregel berechnen.]
Hier noch ein weiteres Beispiel: