Quelle

Geraden im Raum

• Gibt es 12 Geraden im Raum, sodass jede Gerade genau 5 der anderen Geraden schneidet?
• Gibt es 27 Geraden im Raum, sodass jede Gerade genau 10 der anderen Geraden schneidet?
• usw...

Die Schläfli'sche Doppelsechs

• jede rote Gerade schneidet genau 5 blaue Geraden,
• jede blaue Gerade schneidet genau 5 rote Geraden!

Die Konstruktion einer Schläfli'sche Doppelsechs ist ganz einfach, wenn man den Trick kennt.

• Man beginnt mit einem Würfel
• und zeichnet vier der Ecken A, B, C, D aus, die zusammen ein Tetraeder erzeugen.
• Man viertelt die Würfel-Kanten und nimmt die Punkte, die den Abstand 1/4 von den Ecken A, B, C, D haben, dies liefert 12 Punkte auf dem Würfel.
• Verbindet man nun auf den 6 Würfel-Seiten jeweils gegenüberliegende Punkte, so erhält man pro Würfel-Seite 2 Geraden (eine blaue und eine rote), insgesamt also 12 Geraden.
  Bei der Farb-Wahl ist darauf zu achten, dass sich die roten Geraden nicht schneiden sollen (dann schneiden sich auch die blauen nicht).

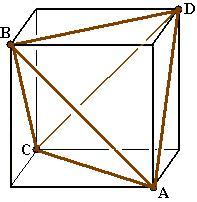
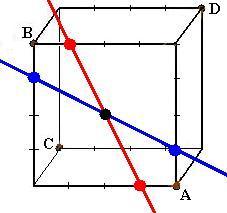
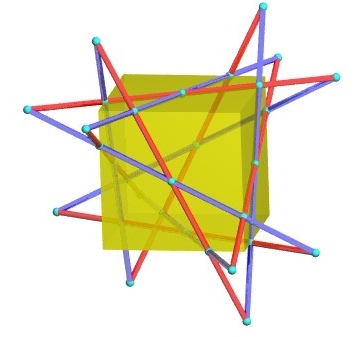
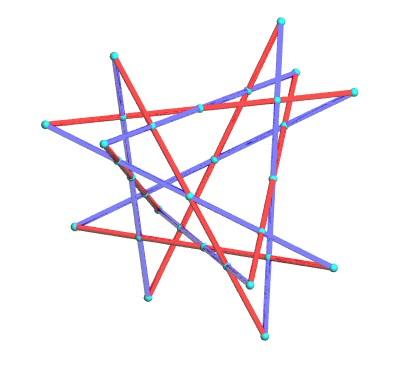
• Es ist leicht zu sehen, dass eine rote Gerade fünf der blauen Geraden schneidet: rot-blaue Geradenpaare, die sich nicht schneiden, liegen auf gegenüberliegenden Würfelflächen.

  Auch das 27-er Problem besitzt eine Lösung: die 27 Geraden auf einer kubischen Fläche in allgemeiner Lage!

  Es gibt einen interessanten Zusammenhang zwischen dem 12-er und dem 27-er Problem: Betrachtet man die 27 Geraden auf einer kubischen Fläche in allgemeiner Lage, so gibt es genau 36 Teilmengen dieser 27 Geraden, die eine Schläfli'sche Doppelsechs bilden.

  Was ist die Bedeutung der Zahl 36 ? Dies ist die Anzahl der positiven Wurzel des Wurzelsystems E₆.

  Freudenthal hat gezeigt, wie man in natürlicher Weise eine explizite Bijektion zwischen den Teilmengen der 27 Geraden, die eine Schläfli'sche Doppelsechs bilden und den positiven Wurzel konstruieren kann.

  Die 28 Doppeltangenten einer ebenen Kurve vierten Grads

  Kubische Flächen

  Seit Descartes (1596-1650) werden viele geometrische Gebilde durch algebraische Gleichungen beschrieben. Die Methode hat den Nachteil, dass es schwierig werden kann, die Gebilde zu visualisieren. Flächen, also zweidimensionale Gebilde, werden dabei (oft) durch Gleichungen in drei Variablen beschrieben.

  Geraden auf Flächen:

  Es gibt vollständig gekrümmte Flächen, bei denen jeder Punkt zu einer Geraden gehört, die ganz in der Fläche liegt, unendliche viele Geraden enthalten, z.B. das einschalige Hyperboloid. Insbesondere enthält eine derartige Fläche unendlich viele Geraden.
  (Dies gilt für jede quadratische Fläche, sofern man mit komplexen Koordinaten arbeitet!

  In einem Briefwechsel zwischen Arthur Cayley (1821-1895) in Cambridge und George Salmon (1819-1904) in Dublin wurde zum ersten Mal notiert, dass auf einer durch eine kubische Gleichung definierten glatten Fläche immer genau 27 Geraden gibt.

  
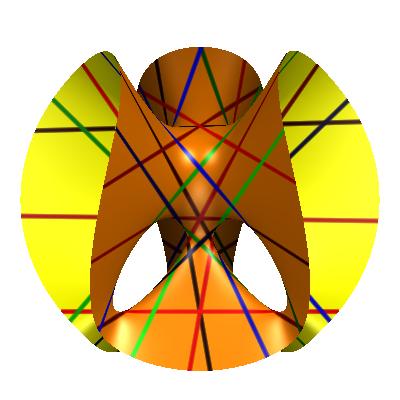
  Oliver Labs

  Es gilt: Jede dieser Geraden schneidet genau 10 der übrigen, und zwar bilden diese 10 Geraden zusammen mit der vorgegebenen Geraden 5 Dreiecke.

  Auf diese Weise erhält man also genau 45 Dreiecke auf der Fläche.

  Beweise

  In vielen Büchern zur algebraischen Geometrie finden sich Beweise.
  • Van der Waerden: Einführung in die algebraische Geometrie Springer Verlag 1939 (und 1973), 148-153.

  Die Clebsche Diagonalfläche

  1861 zeigte Clebsch dass man kubische Fl in the so called pentahedral form.

  Modelle

  Clebsch

  • Das erste Modell wurde wohl von Clebsch angefertigt.
  • Die berümte Sammlung mathematischer Modelle in Göttingen enthät natürlich ein Modell der Cleb'schen Diagonalfläche.
    Darauf wird zum Beispiel im Buch von Van der Waerden A history of Algebra hingewiesen.
  • Kopien dieses Modells wurden in der ersten Häfte des 20. Jahrhunderts vom Teubner-Verlag vertrieben.
  • Ein derartiges Modell wurde als deutscher Beitrag bei der Weltausstellung 1894 in Chicago vorgeführt.
  • Zum 150. Geburtstages von Felix Klein im Jahre 1999 ist eine 2,50 m Kopie der Clebschen Diagonalfläche in der Düsseldorfer Universität aufgestellt worden.

  • Im Rahmen einer Diplomarbeit an der Uni Bielefeld wurden in den 80er Jahren Vorlagen für ein neues Gipsmodell entwickelt, das von Kürpig hergestellt wurde:
    Hier sind nun die Geraden wirkliche Geraden!

  Literatur

  • Weber
  • Felix Klein: Vorlesungen über
  • David Hilbert, Stefan Cohn-Vossen: Anschauliche Geometrie.
  • A. Henderson: The 27 lines upon the cubic surface, Cambridge, University Press, 1911.
  • Jakob Steiner: Crelle's Journal für Mathematik 53 (133-141),
    Siehe auch: Steiner's Werke II, 651-659.
  • Oliver Labs, The Cubic Surface Homepage, Algebraic Geometry Group, University of Mainz, Germany
  • Gerhard Fischer: Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Kommentarband. Braunschweig, Germany: Vieweg, pp. 9-14, 1986.

    ---