Fibonacci Numbers and Linear Algebra.
Claus Michael Ringel (Bielefeld)
Abstract: The famous Fibonacci numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, ...
have attracted a lot of interest in and outside of mathematics.
They play an important role in applications in biology, but also in
computer science and other areas. The lecture will draw the attention to questions in
linear algebra which lead to Fibonacci numbers: we will
give a categorical interpretation of some well-known combinatorial
identities, but also exhibit new partition formulas.
We will consider triples of matrices (with entries in some field k)
of the same shape, or, equivalently, triples of linear transformations say from V to W,
where V, W are fixed vector spaces over k. Such triples are called 3-Kronecker modules.
Trying to classify them, it turns
out that certain 3-Kronecker modules play an exceptional role: we call these
modules Fibonacci modules, since the dimension of the vector spaces involved are
Fibonacci numbers. Given suitable 3-Kronecker modules, there is
a corresponding linear representation of the 3-regular tree. In particular,
this happens for the Fibonacci modules and it displays the Fibonacci numbers
by integral functions on the tree.
In this way we obtain the new partition formulas.
Here is the display for the Fibonacci numbers 8 and 21:
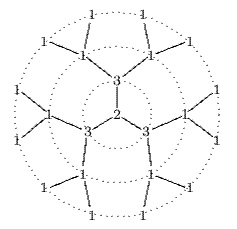
The basic information can be arranged in two triangles, they are quite
similar to the Pascal triangle of the binomial coefficients, but in
contrast to the additivity rule for the Pascal triangle,
we now deal with additivity along hooks. There are intriguing relations
between the two triangles. These relations correspond to
certain exact sequences involving Fibonacci modules, but they can be
verified also recursively.The lecture is based on
joint investigations with Philipp Fahr.
Ringel
Last modified: Jul 16 2013

