Die Menge der ganzen Zahl Z ist eine Teilmenge von R, jede reelle Zahl γ lässt sich in der Form γ = z + γ' schreiben, wobei z eine ganze Zahl und 0 ≤ γ' < 1 ist.
Zahlenpaare, Koordinatensystem. Wir betrachten nun Paare a = (a1,a2) von reellen Zahlen (hier sind a1,a2 also beides reelle Zahlen); solche Zahlenpaare a stellen wir uns als Punkte (oder Vektoren) in der Ebene E =R2 vor: wir arbeiten mit einem Koordinatensystem, das durch die zwei Koordinatenachsen gebildet wird; horizontal verläuft die erste Achse (man nennt sie manchmal die x-Achse), vertikal die zweite Achse (die y-Achse), der Schnittpunkt der beiden Achsen ist der Punkt (0,0), den wir auch einfach mit 0 bezeichnen.
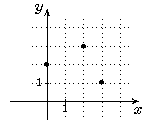
Eingetragen wurden die Punkte (0,2), (2,3) und (3,1), als fette Punkte, zur Verdeutlichung wurde eine Rasterung durch punktierte Linien vorgegeben, solche Rasterungen werden im folgenden eine wichtige Rolle spielen. Den Punkt mit erster Koordinate 2 und und zweiter Koordinate 3 werde ich einfach als (2,3) schreiben, es gibt viele andere mögliche Bezeichnungen. Wenn vom "Vektor" (2,3) die Rede ist, so ist der Vektor vom Ursprung zu diesem Punkt gemeint.
Da Z eine Teilmenge von R ist, ist natürlich Z2 eine Teilmenge von R2, und zwar sind dies gerade die Punkte in der Ebene, die ganzzahlige Koeffizienten haben.
Abstand. Sind zwei Punkte a, b gegeben, so bezeichnen wir mit d(a,b)
den üblichen Abstand, also die Länge der Verbindungsstrecke. Nach dem Satz von Pythagoras ist
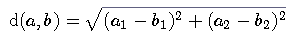
Wir betrachten im folgenden Bewegungen
(auch Isometrien genannt);
darunter verstehen wir abstandserhaltende Abbildungen der Ebene auf sich, also f : R2 → R2
mit
d(f(a),f(a')) = d(a,a').
Warum spricht man von "Isometrien"? Die Ebene E zusammen mit dem hier betrachteten Abstandsbegriff liefert einen "metrischen" Raum, und die Isometrien sind eben gerade diejenigen Abbildungen, die diese "Metrik" erhalten.
Beispiele:
Sei G eine Menge von Isometrien der Ebene E, die eine Gruppe bilden, also
Wir nennen G eine ebene Bewegungsgruppe, falls es in G Translationen ta und tb gibt, wobei a und b von Null verschiedene Vektoren sind, die verschiedene Geraden Ra und Rb erzeugen.
Eine ebene Bewegungsgruppe heißt diskret, wenn es eine positive reelle Zahl ε gibt, so dass gilt: Ist ta eine Translation, die zu G gehört, so ist a = 0 oder |a| > ε.
Hier sollte man innehalten: Es muss nun klar sein, womit sich dieser Vortrag beschäftigt: mit diskreten ebenen Bewegungsgruppen. Wie wir gesehen haben haben, braucht es nicht viel an Vorbegriffen, um die Definitionen zu verstehen, aber dies ist unabdingbar. Und es reicht nicht, nur eine vage Vorstellung zu haben. Was muss man wissen? Was die Ebene E ist, was eine Abbildung E → E ist, was abstandserhaltend bedeutet. Und dann natürlich: was Translationen sind. Aber das ist schon alles. Mathematische Untersuchungen gehen immer so vor: es gibt gewisse Grunddefinitionen, mit denen gearbeitet wird und die man kennen muss. Damit wird dann gearbeitet.
Konstruktionsverfahren für Beispiele: Ist X eine Teilmenge der Ebene E = R2, so sei B(X) die Menge der Isometrien, die X auf sich abbildet. Diese Menge erfüllt wieder die Gruppen-Axiome, also ist auch B(X) eine Gruppe.
Bemerkung: Eine Bewegung g gehört genau dann zu B(X), wenn g(X) = X ist. Betrachtet man die größere Menge aller Bewegungen g, so dass g(X) eine Teilmenge von X ist, so erhält man im allgemeinen keine Untergruppe. Denn nehmen wir zum Beispiel als X die Menge der Punkte (n,0) mit natürlichen Zahlen n, und ist g die Translation g = t(1,0), so ist g(X) Teilmenge von X, dagegen ist h(X) für h = g-1 = t(-1,0) nicht in X enthalten.
Beispiele:
Sei L die Menge aller Punkte a in E, so dass ta zu G gehört. Dies ist eine Teilmenge in E.
Wir nennen einen Vektor a in L minimal, falls a nicht der Nullvektor ist und falls |a| ≤ |b| für jeden von Null verschiedenen Vektor b in L gilt. Eine solche Definition ist immer möglich, besagt aber natürlich nicht, dass es solche "minimale Vektoren" gibt. In unserem Fall gibt es sie aber, wie wir gleich zeigen werden.
Lemma 1. Es gibt in L einen minimalen Vektor.
Gibt es nur einen? Mit Sicherheit nicht. Denn zumindest gilt: Ist a minimal, so auch -a, und diese beiden Vektoren sind ja verschieden! Und wie wir noch sehen werden, wird es oft mehr als 2 minimale Vektoren geben!
Beweis ("Kompaktheitsargument"): Betrachte ein Raster mit Kantenlänge ½ε. Innerhalb jedes Quadrats kann es höchstens ein a geben, das zu L gehört: Sind nämlich a,a' beide in L und liegen sie innerhalb eines Quadrats, so ist ta'ta-1(a) = ta-a'. Aber der Abstand d(a,a') = |a-a'| ist echt kleiner als ε. Demnach ist a = a', da G eine diskrete ebene Bewegungsgruppe ist. Sei nun b ein von Null verschiedenes Element von L. Wähle eine natürliche Zahl mit |b| < nε und betrachte das Quadrat mit den Ecken (nε,nε), (nε,-nε), (-nε,nε),(-nε,-nε). und rastere es: Hier der Fall n = 3:
Das Gesamt-Quadrat zerlegt sich in 16 n2 kleine Quadrate: also gibt es innerhalb dieses Quadrats höchstens 16 n2 von Null verschiedene Punkte, die zu L gehören (aber auch mindestens einen, nämlich b). Alle Punkte außerhalb des Quadrats haben Abstand größer als nε, also größeren Abstand als unser Punkt b. Wir finden also innerhalb des Quadrats einen von Null verschiedenen Punkt a, der kleinstmöglichen Abstand vom Ursprung hat.
Lemma 2. Sei a ein minimaler Vektor. Ist c in L und liegt c auf der Geraden Ra, so ist c ein ganzzahliges Vielfaches von a.
Es gilt sogar die Formel:
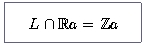
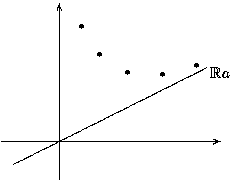
Nun gibt es ein b in L, das nicht zu Ra gehört. Wir wählen ein solches b, das kleinstmöglichen Abstand von der Geraden Ra hat. Auch hier ist wieder zu zeigen, daß es ein derartiges b gibt, denn es könnte ja eine Folge von bi in L geben, deren Abstand von der Geraden R immer kleiner wird, also eine Folge von Vektoren aus L, die sich beliebig der Gerade nähern (linkes Bild). Oder auch (rechtes Bild): dass sie sich beliebig einer Parallelen von Ra nähern, während es im schraffierten Bereich keinen einzigen Vektor aus L gibt:
| 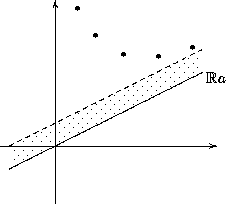
|
Wir fixieren ein b' in L, außerhalb der Geraden Ra und betrachten das von a und b' aufgespannte Parallelogramm P. In diesem Parallelogramm gibt es natürlich wieder nur endlich viele Vektoren, die zu L gehören, und zwar auch solche, die nicht auf der Gerade Ra liegen (nämlich zum Beispiel b', aber auch a+b'). Wähle im Parallelogramm ein b, das zu L, aber nicht zu Ra gehört und kleinstmöglichen Abstand von Ra hat.
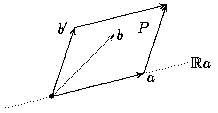
Lemma 3.
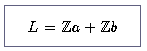
Beweis: Klar ist wieder eine Inklusion: jede ganzzahlige Linearkombination von a und b gehört zu L. Sei nun umgekehrt c in L. Wir schreiben c = γ a + δ b mit reellen Zahlen γ, δ. Schreibe δ = z+δ', dabei sei z eine ganze Zahl und 0 ≤ δ' < 1. Betrachte c-zb = γ a + δ b - zb = γ a + δ'b. Dies ist ein Punkt auf der Geraden R a + δ'b: sie verläuft parallel zu Ra und zwar durch den Punkt δ'b.
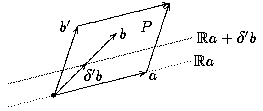
Die Punkte z'a + δ'b mit ganzahligem z' liegen im Abstand |a| auf der Geraden Ra+δ'b, etwa:
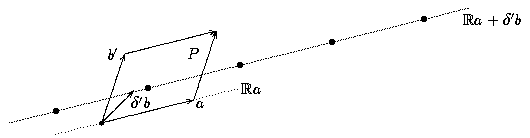
insbesondere muss also einer dieser Punkte im Parallelogramm P liegen. Da dieser Punkt einen kürzeren Abstand von R a hat und zu L gehört, sehen wir, daß δ' = 0 gilt, und demnach ist δ eine ganze Zahl. Es ist also c - zb = γ a ein reelles Vielfaches von a, das zu L gehört. Wir wissen aber schon, daß reelle Vielfache von a, die zu L gehören, ganzzahlige Vielfache von a sind: also ist auch γ eine ganze Zahl. Dies zeigt, daß c eine ganzzahlige Linearkombination von a und b ist.
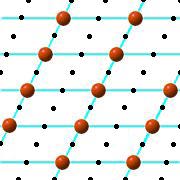
Beachte: Ein Gitter hat nicht nur eine Basis, sondern sehr viele: hier sind einige Basen des Standard-Gitters durch fette Punkte gekennzeichnet:
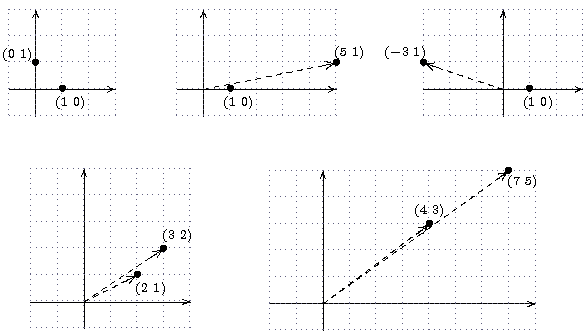
Wie sieht man, dass dies Basen sind? Es gibt ein ganz einfaches Kriterium, um dies zu überprüfen: Die Determinante der Matrix mit den beiden Vektoren als Zeilen muss gleich 1 oder -1 sein. - Es mag auf den ersten Blick verwundern, dass in den beiden unteren Bildern der Winkel zwischen den beiden Basisvektoren sehr klein ist. Das muss aber so sein: denn der Betrag der genannten Determinante ist nichts anderes als der Flächeninhalt des Parallelogramms, das von den beiden Vektoren aufgespannt wird: sind diese Vektoren recht lang, so muss entsprechend der Winkel sehr klein sein, wenn man als Flächeninhalt 1 erhalten soll.
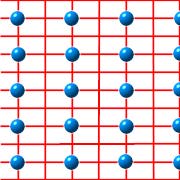
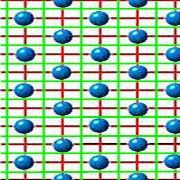
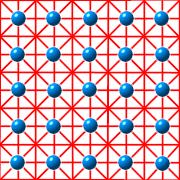
Wenn wir also Bilder von Gittern zeigen, so sollten eigentlich nur die Gitterpunkte markiert sein. Das Zeichnen von "Gitterlinien" ist irrefürend, da es auf der Auswahl einer Basis beruht. Die folgenden drei Bilder zeigen das gleiche Gitter, links nur die Gitterpunkte, rechts daneben einmal mit der Basis (1,0) und (0,1), das andere Mal mit der Basis (1,0) und (2,1):
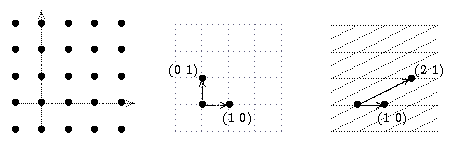
Bisher haben wir mit einem willkürlich gewählten Punkt als Ursprung gearbeitet. Betrachten wir eine beliebige Drehung d in G mit Drehzentrum x, so können wir voraussetzen, dass x der Ursprung ist. Insbesondere ist also d dann linear!
Lemma 4. Ist g in G linear, so ist g(L) = L.
Beweis: Sei a in L, also ta in G. Wir zeigen:
Lemma 5. Sei L ein Gitter im R2. Sei φ eine Drehung um den Urspung, die L auf sich abbildet. Dann hat φ die Ordnung 1,2,3,4, oder 6.
Beweis: Sei g eine Drehung um den Urspung, die L auf sich abbildet.
Ist die Ordnung von g mindestens 7 (oder sogar unendlich),
so erhalten wir auf dem Kreis mit Radius |a| mindestens 7 Punkte,
die alle zu L gehöhren, nämlich die Bilder von a unter
den Potenzen von g. Es muss dann zwei solche Punkte a', a" geben,
so dass der Winkel γ zwischen a',0 und a" echt kleiner als
1/6 ×2π
ist. Dann ist aber der Abstand zwischen diesen beiden Punkten
a' und a" echt kleiner als |a|.
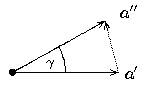
Da mit a' und a" auch der Vektor
a"-a' zu L gehört, dieser aber kleinere Länge als
a hat, erhalten wir einen Widerspruch.
Sei nun g eine Drehung der Ordnung 5. Dann ist zumindest eine Potenz von g
die Drehung dα mit α = 1/5 ×2π.
Mit a gehört auch d2α(a), und damit auch die
Summe a+d2α(a) zu L.
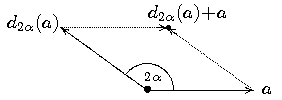
Es ist aber |a+d2α(a)| echt kleiner als |a|, auch
dies also ein Widerspruch zur Minimalität von a.
Zweiter Beweis: Hier verwenden wir Matrizen-Theorie. Sei also g =
dα die Drehung um den Ursprung mit Winkel α.
Man kann jede lineare Isometrie durch eine 2×2
Matrix beschreiben, dabei hängt dies von der Auswahl einer Basis
ab. Unsere Drehung dα wird einerseits durch die
Matrix
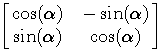
beschrieben (wenn wir die
Standardbasis verwenden), andererseits durch eine
Matrix
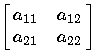
mit ganzzahligen Koeffizienten
(wenn wir als Basis die Vektoren a und b verwenden: wir wissen ja,
dass dα(a) und dα(b) zu L gehören,
also ganzzahlige Linearkombinationen der Vektoren a und b sind).
Wird ein und dieselbe lineare Isometrie durch
zwei verschiedene Matrizen beschrieben, so ist zumindest die "Spur"
dieser Matrizen gleich, also die Summe der beiden Diagonalkoeffizienten.
Die Spur der ersten Matrix ist 2cos(α), die der zweiten ist
a11+a22, also eine ganze Zahl: Wie sehen also,
dass 2cos(α) eine ganze Zahl sein muss, also ist cos(α)
eine der Zahlen -1, -½ 0, ½ 1, und demnach ist α
ein Vielfaches von 45o oder von 60o.
Wie sehen die jeweiligen Symmetriegruppen aus? Es gibt immer Drehungen um 180o, denn die Multiplikation mit -1 ist gerade eine derartige Drehung ("Punktspiegelung"). Im allgemeinen hat kein Gitter keine anderen linearen Isometrien. Gibt es keine weiteren Drehungen, aber Spiegelungen, so handelt es sich um ein Rechteck-Gitter oder ein Rautengitter: im ersten Fall gibt es keine Gleitspiegelungen, um zweiten gibt es solche. Gibt es eine Drehung der Ordnung 4, so liegt das Quadratgitter vor. Gibt es eine Drehung der Ordnung 3, so auch eine der Ordnung 6 (denn es gibt ja immer die Punktspiegelungen), so arbeitet man mit dem Hexagonal-Gitter.
Besser stellt man sich diese 5 Fälle nicht als Liste, sondern in folgender Anordnung vor:
 | ||||
 |  | |||
 |  | |||
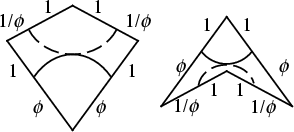
Dieses Diagramm entspricht der kanonischen Anordnung der speziellen Dreiecke (und das muss auch so sein: gegeben sind ja zwei Vektoren a, b, betrachtet wird also das Dreieck mit den Eckpunkten a, Ursprung, b):
-gleichschenklig | ||||
Was heißt hier "verschieden"? Ist G eine Bewegungsgruppe auf E und G' eine Bewegungsgruppe auf E' (ebenfalls eine reelle Ebene), so wollen wir die Paare (E,G) und (E',G') als im wesentlichen gleich ansehen, wenn es eine Isometrie f : E → E' gibt, so dass unter f die Bewegungen in G denen in G' entsprechen (d.h.: zu jedem g in G gibt es ein g' in G' mit g'f(x) = f(g(x)), und man erhält auf diese Weise auch alle Elemente aus G').
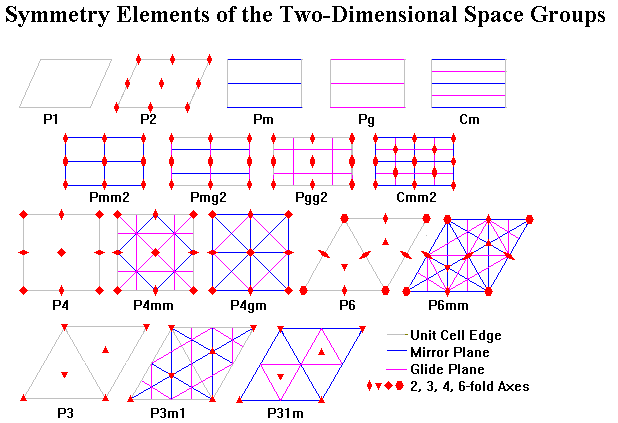
Man nennt diese Gruppen oft auch die ebenen Kristallgruppen, die Kristallographen verwenden folgende Bezeichnungen: p1, p2, pm|p1m, pg|p1g, pmm|p2mm, pmg|p2mg, pgg|p2gg, cm|c1m, cmm|c2mm, p4, p4m|p4mm, p4g|p4gm, p3, p3ml, p3lm, p6, p6m|p6mm
Satz. Sei G eine diskrete ebene Bewegungsgruppe, sei T die Untergruppe aller Translationen. Dann ist T ein Normalteiler in G und G/T ist eine der folgenden Gruppen: Cn oder Dn, mit n = 1,2,3,4, oder 6.
Dabei ist Cn die zyklische Gruppe der Ordnung n, sie besteht aus allen Drehungen um den Ursprung mit Drehwinkel r/n × 2π, dabei ist r eine ganze Zahl mit 0 ≤ r < n. Die Gruppe Dn ist die Diedergruppe der Ordnung 2n, dies ist die Symmetriegruppe des regelmäßen n-Ecks (und Cn ist die Untergruppe der Drehungen in Dn).
Man nennt G/T die Punktgruppe zu G, man kann sie auf folgende Weise direkt erhalten: Jede Isometrie g ist Hintereinanderschaltung einer linearen Isometrie g' und der Translation tg(0), also
Wir betrachten die Zuordnung, die jedem g in G die lineare Isometrie g' zuordnet; dies ist ein Gruppenhomomorphismus von G in die lineare Gruppe GL(2,R), deren Kern gerade T ist. Unter diesem Gruppenhomomorphismus wird G/T mit einer Untergruppe von GL(2,R) identifiert.
Wir kennen nun sowohl T als auch G/T. Es stellt sich also die Frage, wie man aus der Kenntnis von T und G/T die Struktur von G bestimmen kann. Dies leistet die sogenannte "Kohomologie-Theorie" von Gruppen.
| Parkettierungen
(also Muster von Holz-Parketten) | 
| |
| Pflasterungen
(von Straßen und Wegen) (fr.: Pavages) | 
| |
| Tapetenmuster
(engl.: Wall paper) | 
| |
| Ziegel-, Fliesen-, Kachelmuster
(engl.: Tilings) | 
|
Alle diese Vokabeln beziehen sich auf ebene Muster, deren Symmetrie-Gruppe eine diskrete ebene Bewegungsgruppe ist (es gibt also Translationen in zwei verschiedene Richtungen, und die echten Translationsvektoren sind nichtbeliebig klein...)
Owen Jones hat 1856 ein Buch mit dem Titel The Grammar of Ornament herausgegeben, das auf 112 Tafeln unzählige Ornamente aus den verschiedensten Kulturen enthält, insbesondere finden sich darin sehr viele Beispiele von Pflasterungen. Sie sind im Internet aufrufbar: zum Beispiel:
(jeweils mit Information, um welche Bewegungsgruppe es sich handelt).
Wichtig zum Beispiel: Es gibt keine derartigen Muster mit
einer Drehsymmetrie der Ordnung 5.
Sowohl Dürer als auch Kepler haben sich darüber Gedanken
gemacht, wie
Skizzen zeigen. Penrose hat Pflasterungen mit zwei Bausteinen
gefunden, die eine Drehsymmetrie der Ordnung 5 besitzen (sie sind
natürlich notwendigerweise aperiodisch: es gibt keine
Translationen, die sie invariant lassen):
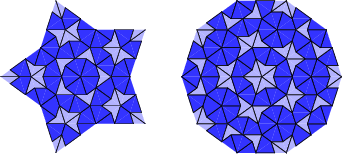
Mit den beiden folgenden Bausteinen (Drachen und Pfeil):
Siehe
Mathworld.
Hier finden sich weitere Abbildungen.
Schließlich noch eine Darstellung aller möglichen
Fundamentalbereiche. Klickt man auf einen der Bereiche, so wird
gezeigt, wie die Gruppe aus diesem Fundamentalbereich die ganze Ebene
rekonstruiert, zum Beispiel im Fall pmm: