Schläfli: 15 weitere Geraden

Wir beginnen mit einer Doppelsechs.

1	2	3	4	5	6	(rot)
1'	2'	3'	4'	5'	6'	(blau)

Wir ordnen dem Paar {1,2} eine neue Gerade zu, die wir 12 nennen, und zwar sei 12 die Schnittgerade der Ebene 1+2' (diese Geraden schneiden sich) mit der Ebene 1'+2 (diese Geraden schneiden sich ebenfalls).

Ingesamt erhalten wir auf diese Weise 6×5/3 = 15 Geraden.

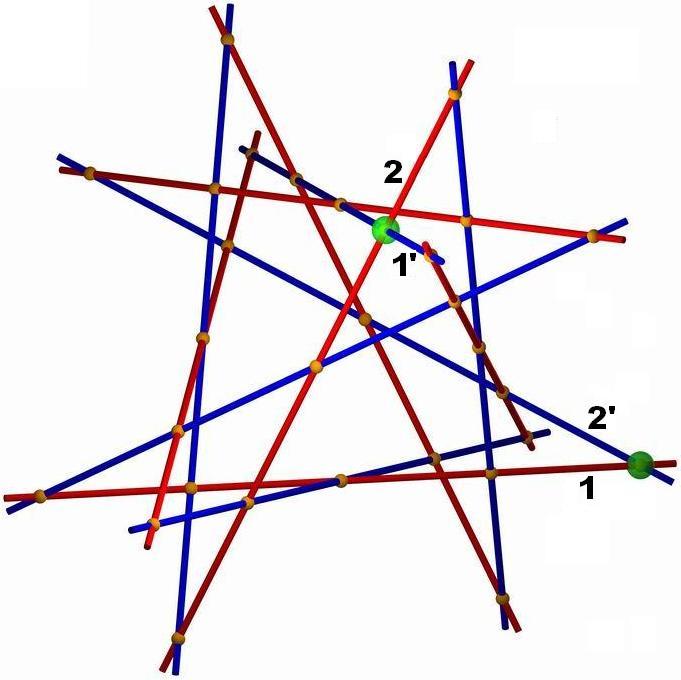
markiert sind die Schnittpunkte der Geraden 1, 2' und der Geraden 1',2.

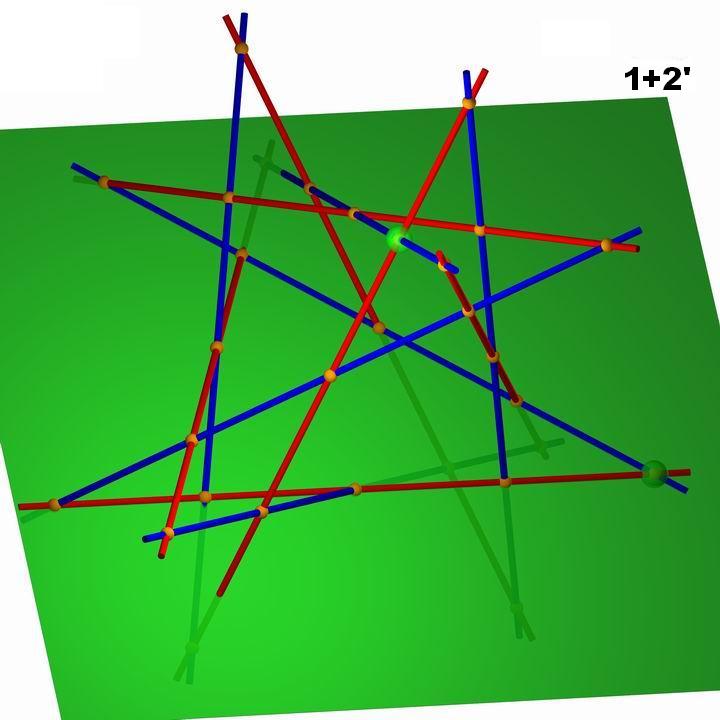
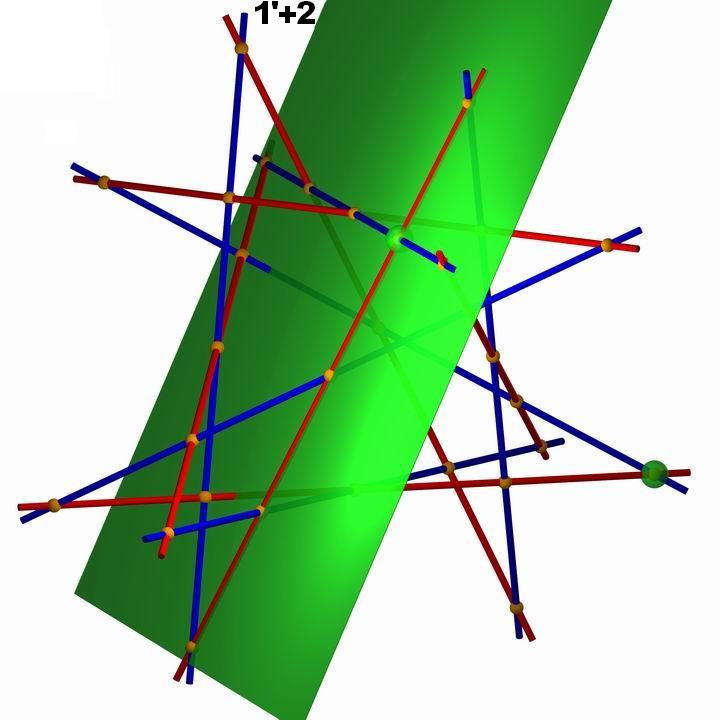
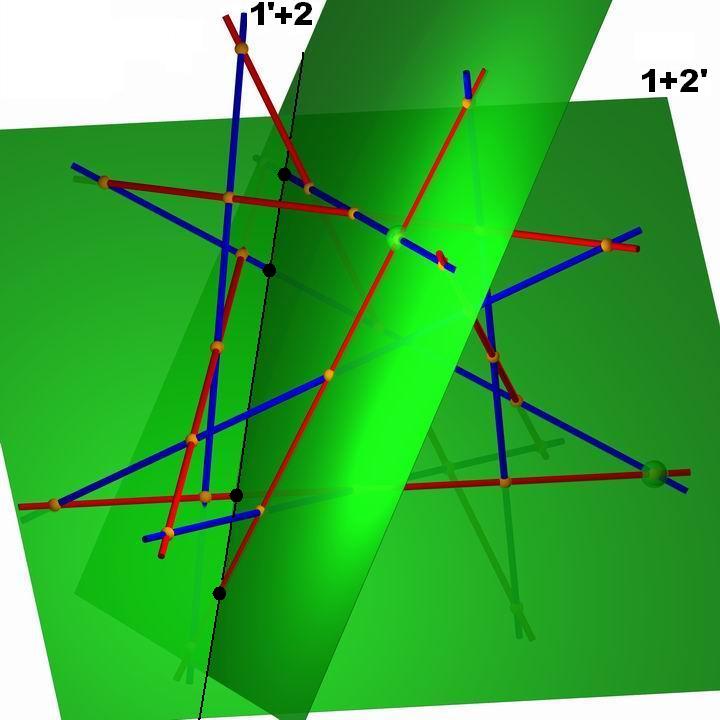
die Ebene durch die Geraden 1, 2' die Ebene durch die Geraden 1', 2 die Schnittgerade

Wir sehen:

• Die Ebene 1+2' enthält nun drei Geraden, nämlich die Geraden 1, 2' und 12.
• Die Ebene 1'+2 enthält ebenfalls drei Geraden, nämlich die Geraden 1, 2' und 12.

Wichtig: Die Gerade 12 schneidet die Geraden 3,4,5,6,3',4',5',6' nicht!

Beweis: Angenommen, 12 und 3 schneiden sich. Dann liegen 1', 12, 3 in einer Ebene (denn sie bilden ein Dreieck); ebenfalls liegen 2', 12, 3 in einer Ebene (auch sie bilden ein Dreieck). Dies ist dann die gleiche Ebene! In dieser Ebene liegt aber zum Beispiel auch 1, daher schneiden sich 1 und 3, Widerspruch.