

|
Satz: Jede Gerade g schneidet genau 10 der übrigen, und zwar liegen
diese 10 Geraden in genau 5 "Dreier-Ebenen" (also in Ebenen, die neben g
noch genau zwei Geraden enthalten). In jeder solchen Ebene gibt es also entweder ein Dreieck aus Geraden, oder drei Geraden, die sich in einem Punkt schneiden. Auf diese Weise erhält man genau 45 Dreier-Ebenen. | 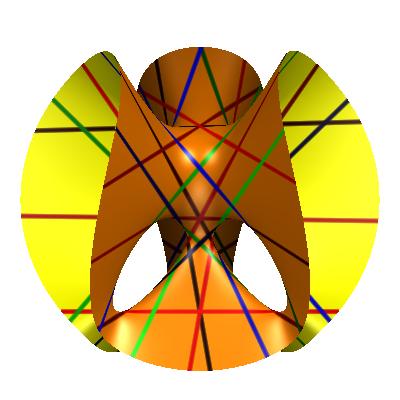 (Oliver Labs) |