Die 28 Doppeltangenten
Wir betrachten Kurven vierter Ordnung in der Ebene, also
die Punkte (x,y) in der Ebene,
die eine Gleichung wie zum Beispiel
erfüllen (die Summe der Exponenten der
einzelnen Summanden soll höchstens 4 sein).
Wir setzen voraus, dass
diese Kurve keine Gerade enthält (das wäre zum Beispiel bei
der Gleichung x2y2 = 0 der Fall).
Jede Gerade schneidet eine
derartige Kurve in höchstens vier Punkten.
Eine spezielle Situation interessiert uns: berührt die Gerade die Kurve
in genau zwei Punkten, so nennt man eine derartige Gerade eine
Doppeltangente.
Man kann nun zeigen: Bei den meisten Kurven vierter Ordnung gibt es
genau 28 Doppeltangenten!
Hier ein Beispiel dieser Geraden-Konfiguration (die Kurve selbst ist rot
gezeichnet):
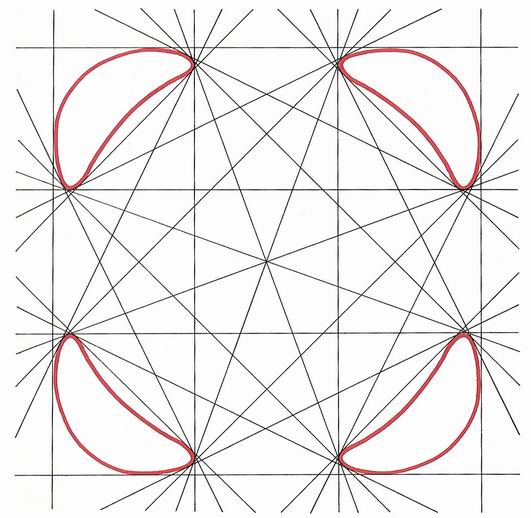
Woher kommt die Zahl 28? Die Kurve besteht hier aus vier nierenförmigen
Komponenten,
- Zu jeder Niere gibt es eine Doppeltangente; dies liefert 4 Doppeltangenten.
- Zu jedem Paar von Nieren gibt es genau 4 Geraden, die beide Nieren
berühren - es gibt 6 Paare von Nieren, also erhalten wir auf diese Weise
24 = 6 x 4 Doppeltangenten.
- Insgesamt erhalten wir also 4 + 24 Doppeltangenten.
Warum interessieren sich Mathematiker für diese Doppeltangenten?
Einer der Gründe ist der folgende:
Ein typisches mathematisches Problem beim Studium von Kurven
besteht darin, Normalformen zu finden: man versucht, ein
geeignetes Koordinatensystem zu finden, um eine möglichst einfache
algebraische Beschreibung zur Verfügung zu haben.
Dieses Normalformenproblem wurde f"ur Kurven vierter Ordnung
im letzten Jahrhundert
dadurch gelöst, dass man nicht
die Kurve selbst, sondern die Konfiguration der
zugehörigen 28 Doppeltangenten untersuchte.
(So führte die Zuordnung einer diskreten Struktur
(bestehend aus nur 28 Elementen)
zur Lösung eines relativ schwierigen nicht-diskreten Problems.)
Der Zusammenhang mit den 27 Geraden einer kubischen Fläche F
Siehe Geiser!
- Man nimmt einen Punkt A auf der Fläche F, der auf keiner der 27 Geraden liegt
und betrachtet alle Tangenten von A an die Fläche F, die nicht zur Tangentialebene
T gehören. Dies ist ein Kegel, der durch ein Polynom vom Grad 4 definiert wird
(das kann man nachrechnen).
- Schneidet man diesen Kegel mit einer Ebene E, die A nicht enthält,
so ist diese Schnittmenge eine Kurve C vom Grad 4.
- Verbindet man jede der 27 Geraden auf F mit A, so erhält man
jeweils eine Ebene, deren Schnitt mit E eine Doppeltangente an C liefert.
- Der Schnitt von T mit E liefert eine weitere Doppeltangente an C.
- Dies sind genau 27 + 1 = 28 Doppeltangenten - und mehr gibt es nicht.
Der Zusammenhang mit dem Wurzelsystem E7
Siehe Freudenthal.
Literatur
- M. Geiser: Über die Doppeltangenten einer ebenen Kurve vierten Grades. Math. Ann I, p.129-138.
- Heinrich Weber: Algebra II. 1896.
Siehe Abschnitt 13.
Dies war das Standard-Algebra-Lehrbuch um die Jahrhundertwende und
im ersten Drittel des 20.Jahrhunderts.
- Hans Freudenthal: The connections between the E7-geometry and the
configuration of the 28 double tangents to the curve of order 4.
Russ. Math. Surv. 31, 1976, p.62-66

