- 10 Eckardt-Punkte, und
- 105 Punkte, in denen sich
genau zwei Geraden schneiden.
105 × 2 + 10 × 6 = 270 = 27 × 10).
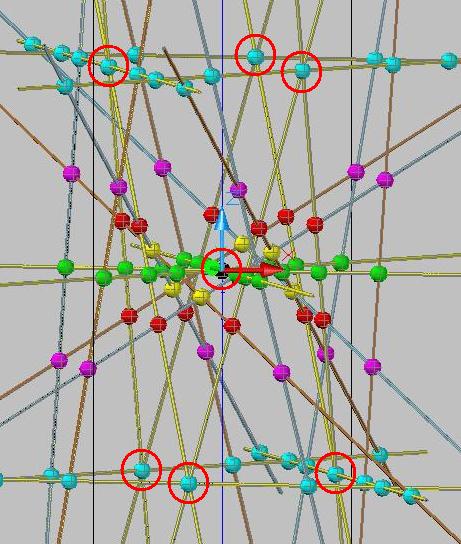
(3 weitere liegen im Unendlichen).
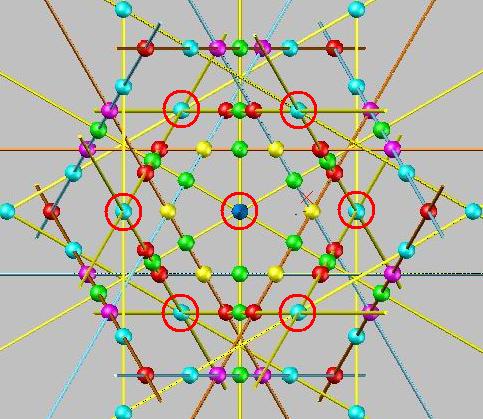
In diesem Fall gibt es
105 × 2 + 10 × 6 = 270 = 27 × 10). |

(3 weitere liegen im Unendlichen). 
|