Banff

C.M.Ringel:
What is known about invariant subspaces of nilpotent operators? A survey. I

General Considerations

1. Normalization

Let P(a,b) be the picket with dimension pair (a,b).

We use P(1,1) as marking γ = 0 (the "zero slope")

Consider for a > 0 the middle term (V,T,U) of the non-split exact sequence
0 → P(a,0) → (V,T,U) → P(0,a) → 0.
The partition of (V,T) is (a+1,a-1).

For n odd, the middle term has "slope" 0,
For n even, the middle term has "slope" 1.

2. Some autoequivalences of the stable category of S(n)

Recall: S(n) is a Frobenius category
with two isomorphism classes of indecomposable proj-inj objects: P(0,n) and P(n,0).
Heller: The stable category of a Frobenius category is a triangulated category.

4 important constructions:

The shift of the grading.
The susspension Σ,
it yields the translation functor of the triangulated category.
The Auslander-Reiten translation τ.
The Serre functor S.

In which way are these functors interrelated?

First formula (Happel):

S = τΣ

The Serre functor S for the stable category:
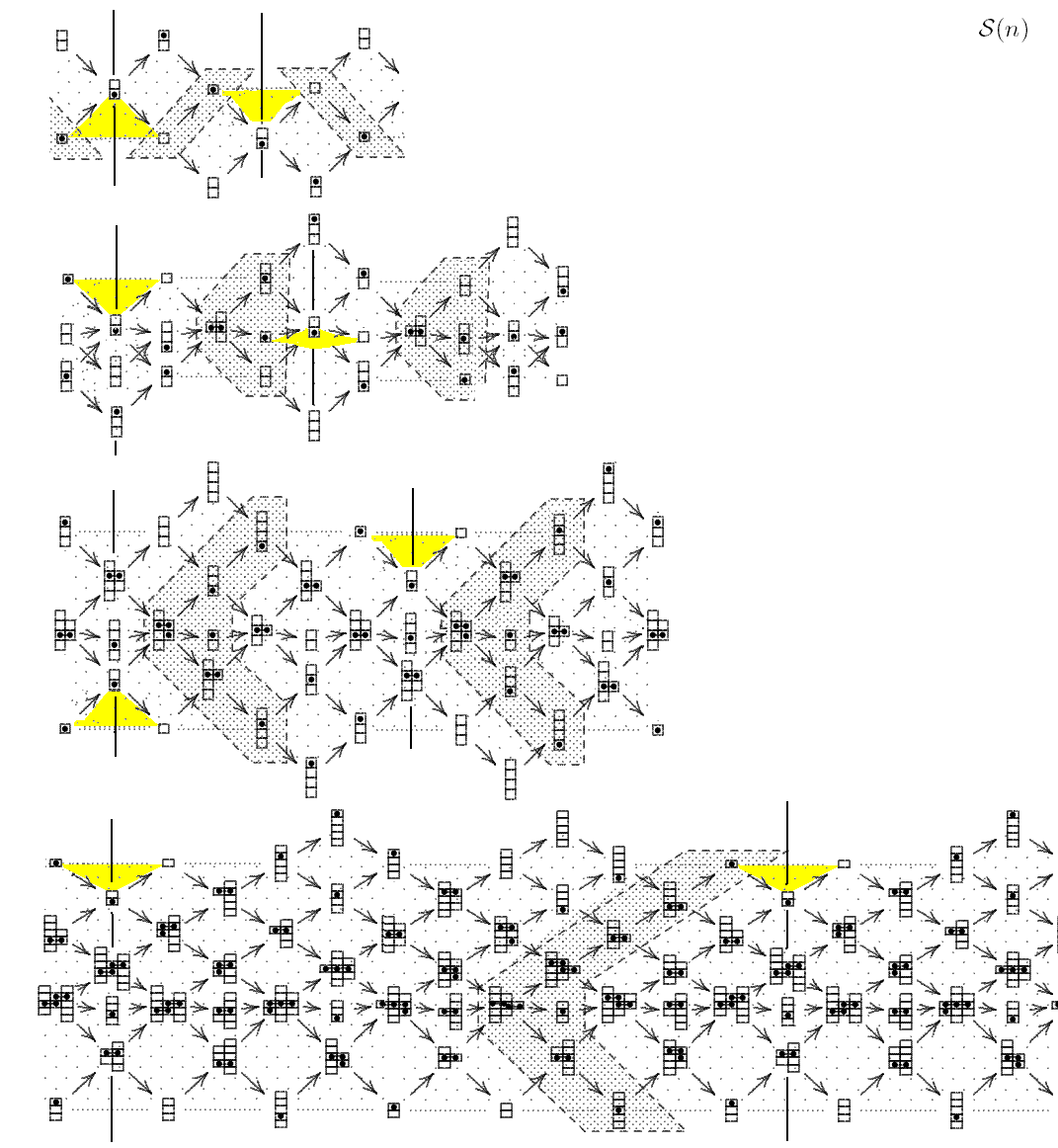
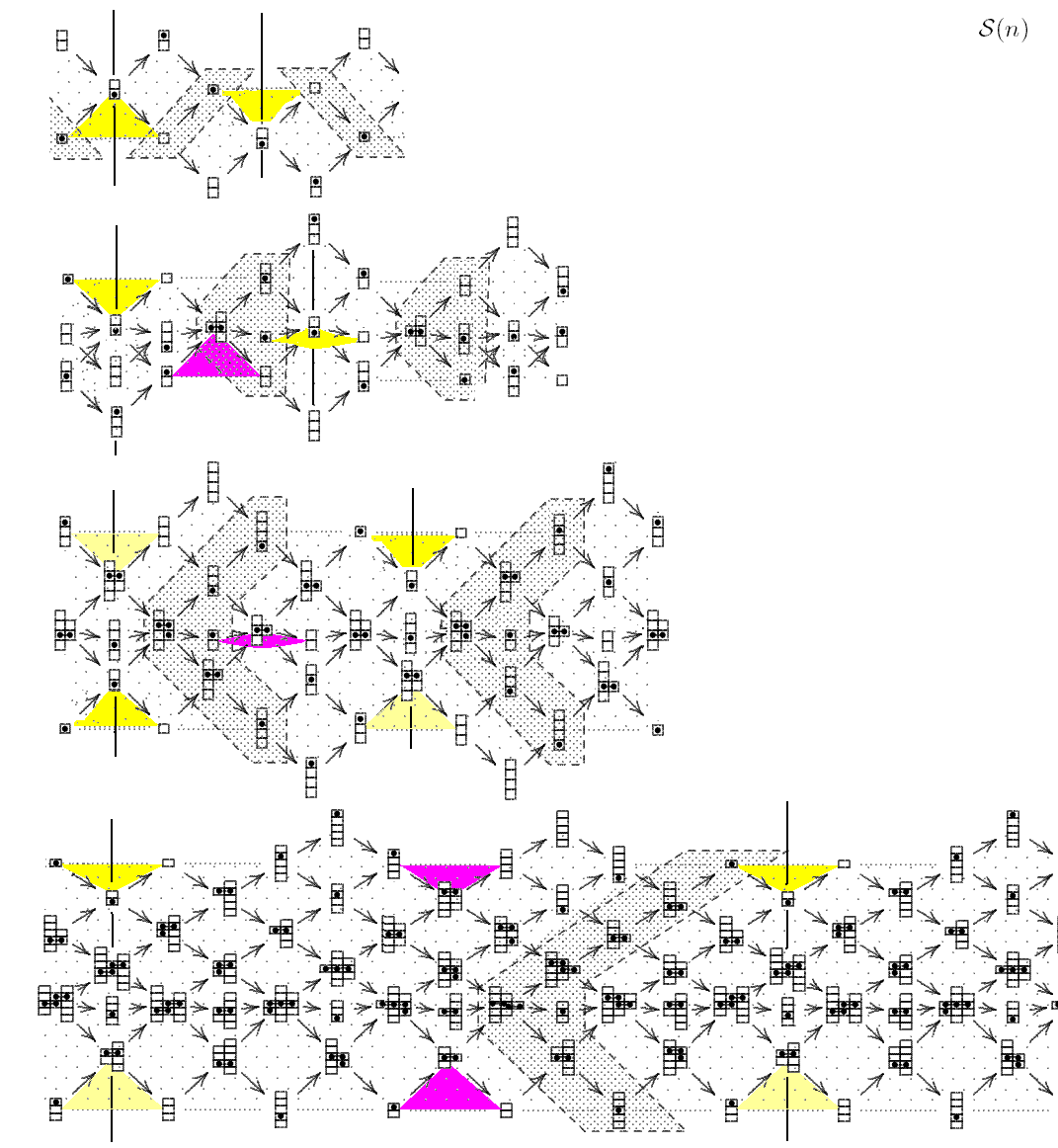
Look at the hammocks (well-known for ZΔ, see already Gabriel).

Relation between the Auslander-Reiten translation τ and the shift:

Second formula.

τ⁶ = (shift)^n-6

Interpretation: For n < 6, the shift is in the direction of τ^-,
for n > 6, the shift is in the direction of τ⁺;

Bold interpretation: We try to rewrite the second formula as

(shift) ~ τ^6/(n-6)

and the numbers 6/(n-6) are just 3/2, 2, 3, 6, ∞, which were used to describe the number of indecomposables in S(n).

2 + 6/(n-6)× 2(n-1)

Let us exhibit the values of the formula for n ≤ 13

n 2 + 6/(n-6)×2(n-1)
1 2
2 5
3 10
4 20
5 50
6 ∞
7 -70
8 -40
9 -30
10 -25
11 -22
12 -20
13 -130/7
... ...

n	2 + 6/(n-6)×2(n-1)
1	2
2	5
3	10
4	20
5	50
6	∞
7	-70
8	-40
9	-30
10	-25
11	-22
12	-20
13	-130/7
...	...

The meaning of the negative number is not clear at all.

Also, it seems to be curious that many of these numbers are divisible by 5.

Of course, 2 + 6/(n-6)×2(n-1) = 10n/(6-n), but a direct Interpretation of this formula is not known.

Relation between the suspension Σ and the shift:

For example, the suspension functur Σ has the property Σ P(a,0) = P(n-a,0) for a > 0.

Illustration for a = 1.

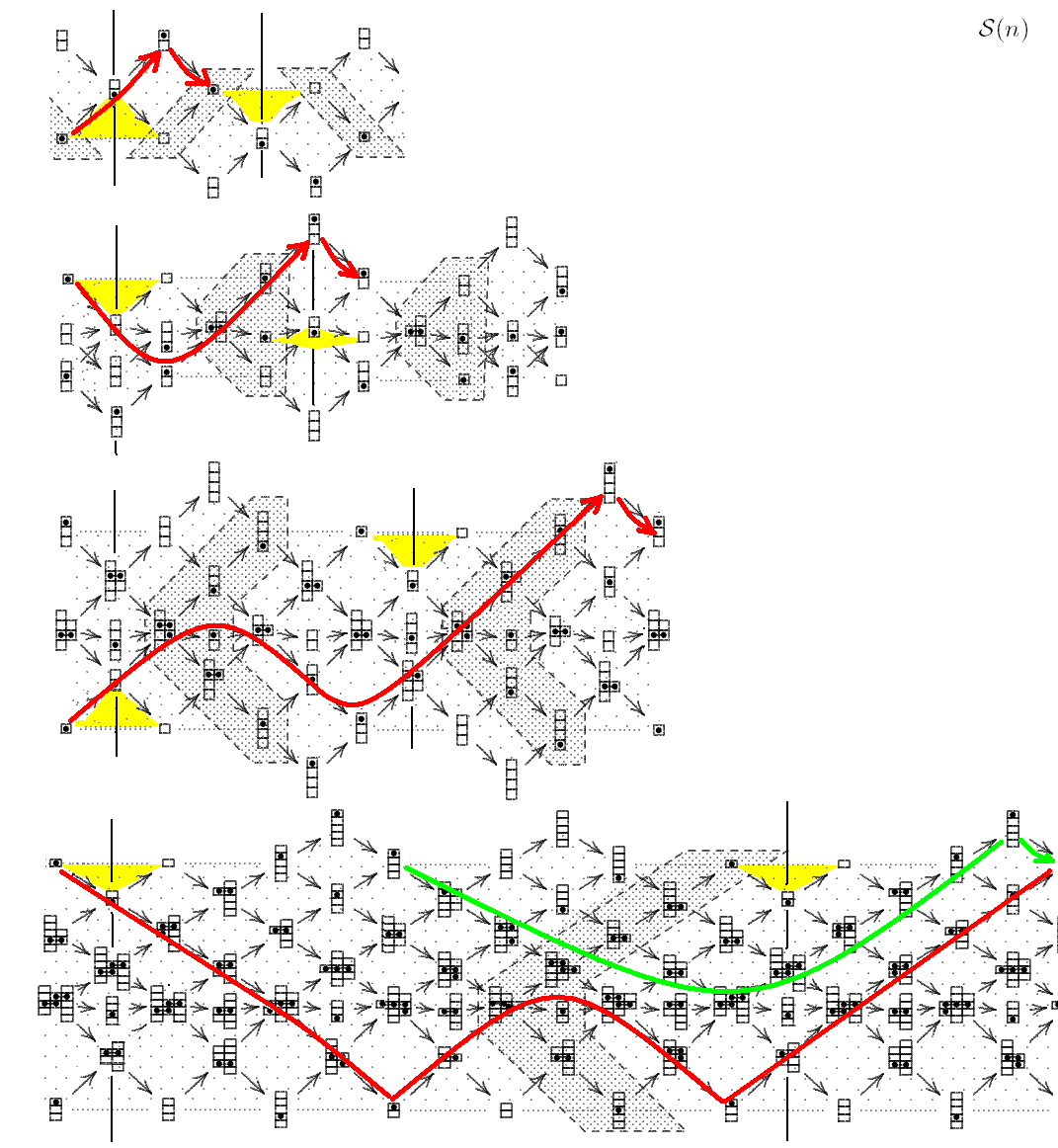
We see: with growing n, the length of the hammock grows fast.
Precise formula later. First a formula for Σ²:

Formula:

Σ² = (shift)ⁿ

Better:

Third formula:

Σ = (shift)³τ³

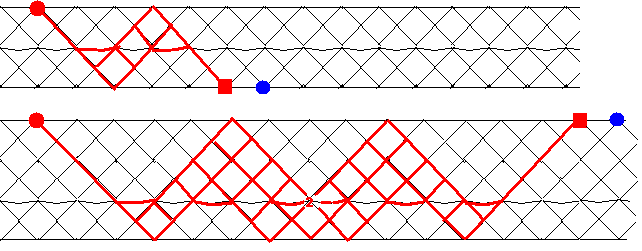
Illustration: Apply τ³ to P(1,0).
This concerns the boundary of the non-stable component.
Claim: τ³P(1,0) is P(n-1,0), shifted appropriately.

Here, we only have to look at three AR-sequences: the (n-1)-(n-1)-seuquence (first: left term is P(n-1,0), right term is P(0,n-1), middle term has as total space (n-2,n)); second: the AR-squence whose middle term has P(0,n) as direct summand - left term is P(0,n-1), right term is P(1,n-1); third the AR-sequence with left term P(1,n-1) and right term P(1,0).)

Here the case n=7 (for any n > 3, only the parts above the water-line change, the part inside the water remains as depicted).

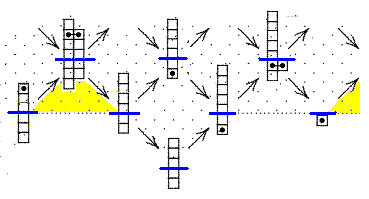
The second and the third formula imply together the formula for Σ²: Proof:

Σ² = (shift)⁶τ⁶ = (shift)⁶(shift)^n-6 = (shift)ⁿ

Calabi-Yau

We obtain the following Calabi-Yau formula

S³ⁿ = Σ^4n-6

Proof: S³ⁿ = τ³ⁿΣ³ⁿ = Σⁿ(shift)^-3nΣ³ⁿ = Σⁿ Σ^-6 Σ³ⁿ = Σ^4n-6 (where we have used first the first formula, then the third, and finally the second).

n 2 3 4 5 6 7 8 9 10 ... lim
power of Σ 4n-6 4 12 20 28 36 44 52 60 68
power of S 3n 12 18 24 30 36 42 48 54 60
Calabi-Yau-dimension
(4n-6)/(3n) 1/3 2/3 5/6 14/15 1 22/21 13/12 10/9 17/15 4/3

	n	2	3	4	5	6	7	8	9	10	...	lim
power of Σ	4n-6	4	12	20	28	36	44	52	60	68
power of S	3n	12	18	24	30	36	42	48	54	60
	Calabi-Yau-dimension (4n-6)/(3n)	1/3	2/3	5/6	14/15	1	22/21	13/12	10/9	17/15		4/3