Canonical

Survey on common knowledge (not all has been published)
also: on open problems.

Definition: Canonical algebra.

Basic terms for canonical algebras:

The tubes, their rank, left rank, right rank, the mouth, the wings
Separating property.

Separating substructures

Note: By definition, the piecewise hereditary algebras are those finite dimensional algebras B such that D^b(mod B) is equivalent to D^b(H) for some hereditary category H, and then D^b(mod B) is equivalent to D^b(mod A) for A a finite dimensional hereditary algebra or to D^b(mod C) for C a canonical algebra.

Thus, in order to understand mod B, one needs to look at the module categories of finite dimensional hereditary algebras and of canonical algebras. These are the algebras which have

either a complete slice,
or a separating tubular family.

The algebras tilted from a finite dimensional hereditary algebra or from a canonical algebra are the quasi-tilted algebras.

Here one should mention the T

Why are the canonical algebras canonical?

Wiktionary (deutsch)

Informatik: allgemeingültige und eindeutige Bezeichnung eines Datensatzes
Mathematik: bezeichnet eine Darstellung in Normalform

Meyers Lexikon online:

Physik: Bezeichnung für nach einer festen Regel gebildete Größen, Operationen u. a., die für die Beschreibung eines physikalischen Vorgangs am besten geeignet sind.

Wikipedia (english):

Basic, canonic, canonical: reduced to the simplest and most significant form possible without loss of generality, e.g., "a basic story line"; "a canonical syllable pattern."
Mathematicians have for perhaps a century or more used the word canonical to refer to concepts that have a kind of uniqueness or naturalness, and are (up to trivial aspects) "independent of coordinates."
Remark: Note that "tilting" means changing coordinates!

Religion24.net

Kanonische Schriften gelten im kirchlichen Sinne als verbindlich. Nach ihnen muss sich jeder Gläubige richten.
Ein Kanon war ein Holzstab, der im antiken, athletischen Wettkampf zur Messung der Sprungweite der Athleten diente.
(canon = a wooden stick for measuring the leap for jumping athlets)

Let me change the title:

In which way are the canonical algebras canonical?

We consider a special class: the tame concealed algebras.

The importance of this class of algebras is well-known

see the Bongartz criterion.
they can be classified: this was done by Happel and Vossieck.
Gabriel wrote in his Bourbaki lectures on rep-finite self-injective algebras: The relevance of this class comes from the fact that they have been classified by Riedtmann.
The T

The domestic canonical algebras form just the crossing of the T:
Horizontally, the hereditary algebras are exhibited,
Vertically the canonical ones.

Aim: In any derived equivalence class, one wants a representative - just one.

Main observation. Any derived equivalence class of domestic canonical algebras contains usually many hereditary algebras, but just one canonical algebra.

First attempt: To choose one hereditary algebra

This means: to choose one orientation.

Clear for type A: one sink, one source (but this is actually a canonical algebra)
Clear for types E: take the subspace orientation
But why not the factor space orientation?
Types D: For n=4 one would like to take the subspace orientation.
But there is nothing similar for n > 4.
For any n one could take: two sinks with distance 2, two sources with distance 2
(at least self-opposite).

Not really convincing.

Remark: Simson-Skowronski call these quivers the "canonically oriented Euclidean quivers".
They need these orientations for case-by-case proofs.

The HV-list

Reprinted in various publications, with different ordering.

Happel-Vossieck. Manuscr. Math. 42 (1983), 221-243
also in SLNM 1099
Bongartz. Math. Ann. 269 (1984), 1-12
Von Hoehne. Commentarii Math. Helv. 63 (1988), 312-336.
Bautista-Gabriel-Roiter-Salmeron. Inventiones Math. 81 (1985), 217-285.
Chaotic: Except for type A, the canonical algebras are missing.
Simson-Skowronski. vol II.

References, in particular:

Aslak Bakke Buan, Idun Reiten, and Ahmet I. Seven: Tame concealed algebras and cluster quivers of minimal infinite type Journal of Pure and Applied Algebra, 211 (2007) 71-82.

The tilting order of the tame concealed algebras: We need a notion: down-tilting: the tilting pair (X(T),Y(T)) splits.

Definition of the poset ?? (Use of Gabrielov transformations?),
There are unpublished investigations of Vossieck. See also von Hoehne.
An important invariant: the shortage = the number of lost (= mixed) indecomposable modules

Domestic canonical algebras

General notation:

₀

₁

₀

Part I. Properties

1. The positive radical generator d

d_i = 1 for all i.

|d| = n.

Formulation in terms of modules:

There exists an indecomposable module M of length n with self-extensions.

RED Up to shift and symmetry, there is only one tilting set in ZΔ which contains only objects in the extension orbits.

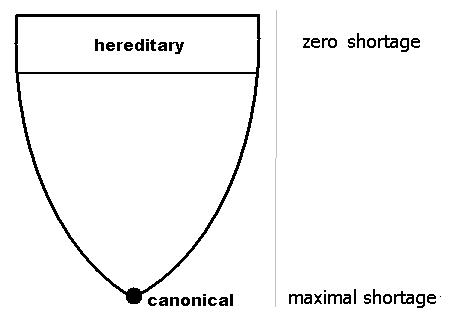
2. Shortage

Let T be a preprojective A-tilting module, A hereditary. The shortage of T or End(T) is the number s(T) of isoclasses of mixed modules.

Remark: The mixed modules have defect < -1.

Proof: They are extensions of two non.zero preprojective modules.

Note: The shortage is 0 iff End(T) is hereditary.

The shortage is maximal.

Tubular type	A_pq	D_n	E₆	E₇	E₈
Maximal shortage	0	binom(n-2,2)	13	43	164

s(Δ) = ∑_{x in Φ+} max x_i - |Φ+|

₀

Ordering of the Happel-Vossieck list according to shortage:

Mottation ordering using the Bongartz complement: Consider preprojective tilting modules containing at least one projective summand, delete a summand such that no propersuccessor is a summand, and add the Bongartz complement.

Sprungweite ist größt-möglich - greatest possible leap.
Also we see nicely the leaps.
The canonical configurations:

3. Sinks and sources

There is only one sink and only one source.

Reformulation:

only one simple module is projective, only one simple module is injective.

C is non-Schurian

This means: we see the Kronecker. Here, we should stress the importance of the exceptional pair (t₀,t_∞) in ZΔ with dim Hom(T₀,T_∞) = 2.

RED: Up to shift and symmetry, there ist just one exceptional pair (t₀,t_∞) in ZΔ with dim Hom(T₀,T_∞) = 2.
And it can be completed in ZΔ to a tilting set in only one way.
One may call this a canonical pair.

What means the 2?

Increase of one component when reflecting.
2-Kronecker pair

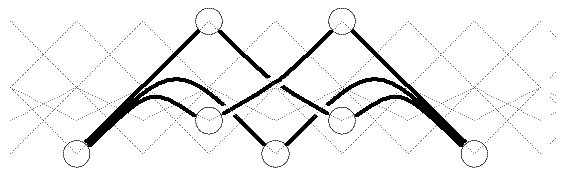
Here, the tubular type E₆. First, the calculation of the hammock for an extension vertex:

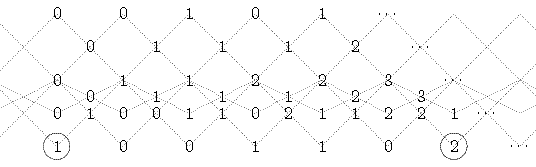
Then the unique completion to a tilting set:

Next, the tubular type E₇. First, the calculation of the hammock for an extension vertex:

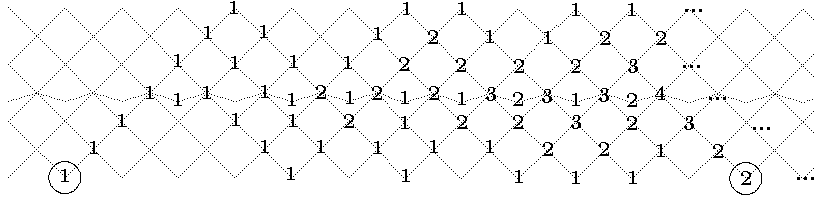
Then the unique completion to a tilting set:

And the tubular type D₈. First, the calculation of the hammock for an extension vertex:

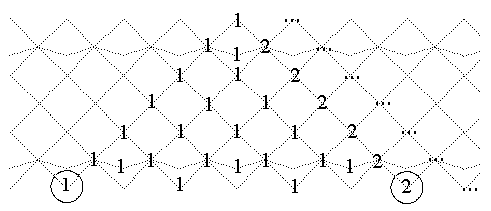
Then the unique completion to a tilting set:

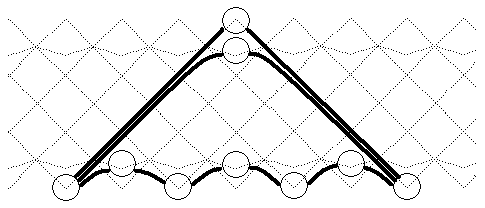
4. Simple regular modules

Any tube of rank r contains r-1 simple modules.

All but 2 simple modules are regular.

₄

Experienced mathematicians know for each extended Dynkin diagram which of the vertices can be considered as the extension vertex -
But looking at the quiver of the canonical algebra, no guessing is needed.

5. 2-Kronecker pairs

We call a pair of B-modules (X,Y) an n-Kronecker pair, provided this is an orthogonal pair of bricks and dim Ext¹(Y,X) = n
(thus, the category of B-modules M with an exact sequence 0 → X^a → M → Y^b → 0 is equivalent to the category of 2-Kronecker modules).

For a canonical algebra, the structure of all Kronecker pairs (X,Y) is obvious:

the module X is preprojective and colocal,
the module Y is preinjective and local,
dim X + dim Y = d.

The number of such pairs is ∏ p_i.

There is a 2-Kronecker pair (X,Y) with X simple

There is a 2-Kronecker pair (X,Y) with Y simple.

Actually: Characterizations

Theorem: For A tame concealed, any of these properties is equivalent to being canonical.

These characterizations concern smallness or largeness of some invariants.

Small:

|d| = n
d_i = 1.

Large:

shortage
the length of the Scheuer hammock (later)

To repeat: Direct display of important properties and invariants

We can read off information:

The positive generator of the radical of the quadratic form.
The tubular type.
The simple regular modules.
Numerical criterion for preprojective - regular - preinjective: x₀-x_∞ (just two non-zero coefficients).
The 2-Kronecker exceptional pairs. For the canonical algebras, this number is p = ∏p_i.
The lengths of preprojective serial modules which are maximal (i.e. not a proper subfactor of a serial module) are p₁, ..., p_t,
The lengths of preinjective serial modules which are maximal are p₁, ..., p_t,
The lengths of regular serial modules which are maximal are p₁-1, ..., p_t-1,

Part II. The ideal lattice of a canonical algebra

Let us look at I = left-socle ∩ right-socle of C.

This is a two-sided ideal of dimension 2, any subspace is a two-sided ideal again,
Thus: The ideal lattice of C is not distributive.
We also can do the following: Let e = e₀+e_∞. Then eCe is the 2-Kronecker algebra.
Here we deal with an idealizer.

There are q+1 one-dimensional ideals I_λ such that C/I_λ has at least one sincere indecomposable module M_λ.
The module M_λ may not be faithful.
Actually: The number of sincere indecomposable C/I_λ-modules is precisely p(λ).
Thus: we recover the canonical configuration p:P(k²) → N₁ looking at the set of ideals I in rad C such that C/I has a faithful module.
Consequence:

C has sincere indecomposable modules which are not faithful.

Recall Jans: On indecompsable representations of algebras. Annals Math. 66 (1957), 418-239.

If the ideal lattice of an algebra C is not distributive, then C is of rep-infinite.
Thus, Jans asserts: canonical algebras are rep-infinite.
These are the only tame concealed algebras which were known quite early to be of infinite representation type.
By the way: The first Jans condition + preprejective tilting yields all what one needs for the Bongartz criterion.
Also note: If we deal with a minimal rep-infinite algebra with non-distributive ideal lattice, then this concerns the socle...

Part III. Further Characterizations

6. Diamonds

In case the base field has at least 3 elements:
There is sincere diamond.

7. Local modules

There is a 1-parameter family of local modules

Brauer-Thrall 1+1/2 implies: strongly unbounded representation type.

There are local modules with self-extensions.

We obtain indecomposable Prüfer modules with local factors.

7*. Colocal modules

There is a 1-parameter family of colocal modules

There are colocal modules with self-extensions.

8. Projective modules

Every indecomposable projective module has defect -1.

This means: it can be embedded into the generic module such that the factor module is a direct sum of Prüfer modules.

There exists an indecomposable projective module which is not thin.

8*. Injective modules

Every indecomposable injective module has defect 1.

There exists an indecomposable omjective module which is not thin.

9. Generic module

If M is the generic module, then M_α is bijective, for any arrow α.

10. Indecomposable modules which are thin and sincere

The number of such modules is

0 if there exists a zero relation,
1 if there are only commutativity relations and the algebra is not canonical,
≥ |k|+1 if the algebra is canonical.

Part IV. Cluster-tilted algebras

Tilted algebras are no longer considered as basic objects,
they are just special factor algebras of cluster-tilted algebras.

Our characterizations dealt with tilted algebras.
Question: Are there similar characterizations of the corresponding cluster tilted algebras?

The cluster-tilted algebras for the canonical algebras:

One additional arrow ω → 0.

Important: The shortage is the number of mixed modules for the corresponding cluster tilted algebra.

The mixed modules for the cluster tilted algebra is a hammock,
namely the hammock of all indecomposable modules for the cluster tilted algebra which are not annihilated by the additional arrow
(this is the Scheuer hammock for the indecomposable length 2 module with composition factors 0 and ω)

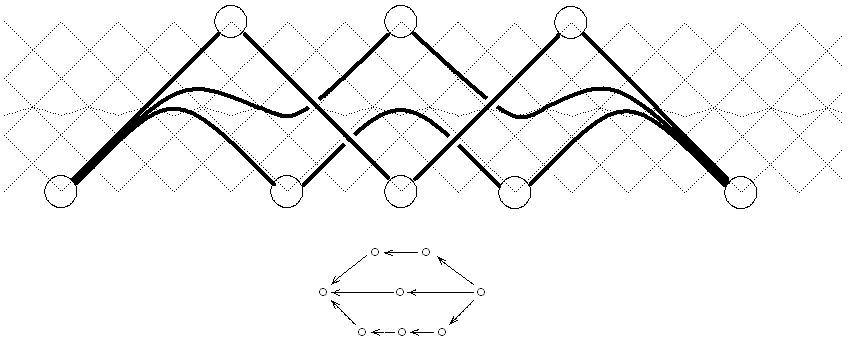
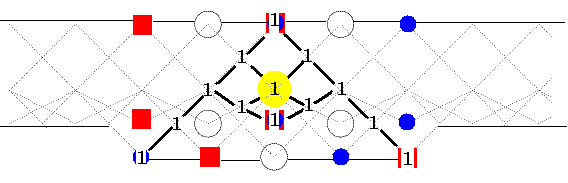
As an example, the tubular type E₆. First, the canonical tilting set:

The transjective component of the cluster tilted algebra is obtained from ZΔ by factoring out this tilting set.

This yields projective vertices (blue circles) and injective vertices (red squares):

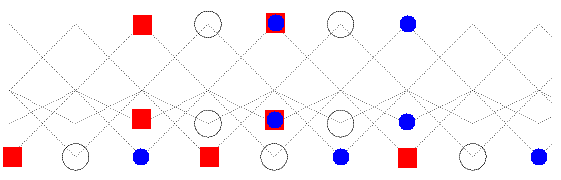
The Scheuer hammock for the mixed modules, it starts at P(ω) and ends at Q(0):

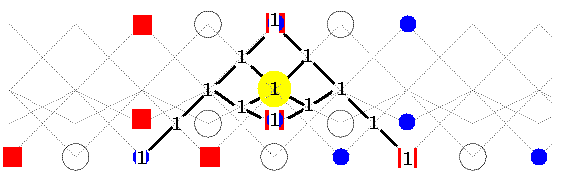
The yellow spot marks the indecomposable length 2 module with composition factors 0 and ω

Here is the Scheuer hammock for the algebra defined by the subquiver

Next, the tubular type E₇. First, the canonical tilting set:

Here is the Scheuer hammock for the mixed modules, it starts at P(ω) and ends at Q(0):

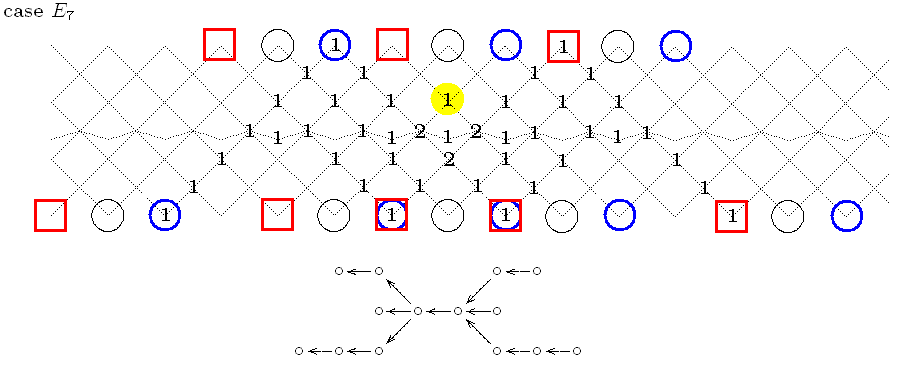
The yellow spot marks again the indecomposable length 2 module with composition factors 0 and ω.

Note:

RED: We obtain the cluster-tilted algebras in the following way:

Take a cluster category C
take a cluster-tilted object T in C,
and form End(T) in .

Here we are dealing with the case

C is of Euclidean type
all summands of T are transjective.

An obvious interesting invariant is the maximal length l of a non-sectional path from some T_i to some T_j.

For End(T) hereditary, this invariant is 0,
For the canonical (cluster-)tilting objects, this invariant becomes maximal.

Here is the list of the maximal values:

Tubular type	A_pq	D_n	E₆	E₇	E₈
Maximal length	0	2(n-2)	12 (=3×4)	24 (= 4×6)	60 (= 5×12)

Here we see zhe number and the length of the leaps...

One further argument

Consider a canonical algebra C.

The proof of the separation property is easy.
The relationship with the Kronecker algebra is completely clear.
Also: easy extension to non-algebraically closed fields.

Squids

Brenner-Butler
Crawley-Boevey
Now: Henning

There is a left squid and a right squid, this yields non-regular tubes.
There is an obvious transition: left squid - canonical - right squid,
look at the repetitive algebra for
Note: generalizations of the squids (as well as of the canonical algebras) are nice for dealing with repetitive algebras

Recall:

RED: Essentially, there is only one tilting set in ZΔ which contains only objects in the extension orbits.
Also, essentially, there is only one canonical pair in ZΔ, and this pair has a unique completion inside ZΔ to a tilting set.

Of course, the squids also use the canonical pair, but here the completion is done outside of the component.

Tilted algebras

It seems: The only tilted algebras with q(1,...,1) = 0 are the canonical ones.

The canonical algebras should be considered as "canonical" for the appearance of a rational 1-parameter family of bricks.

0	if there exists a zero relation,
1	if there are only commutativity relations and the algebra is not canonical,
≥ \|k\|+1	if the algebra is canonical.