Methoden der Analysis zeigen:
Für alle n ≥ 68 ist die Ungleichung falsch.

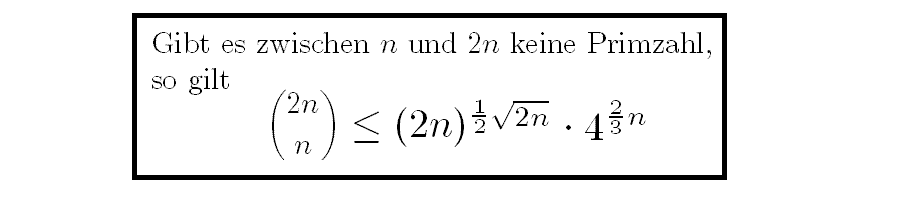
Dies ist eine Aussage, die nichts mehr mit Primzahlen zu tun hat:
eine Vergleichsrelation zwischen zwei Funktionen.
Methoden der Analysis zeigen:
|

|
Damit ist gezeigt (durch Widerspruch):
Ist n ≥ 68, so gibt
es eine Primzahl p mit n < p ≤ 2n.
Zusatz:
Für n ≤ 67 findet man mühelos solche Primzahlen,
also gilt das Bertrandsche Postulat für alle n.