• die 5 platonischen Körper (Tetraeder, Oktaeder, Würfel, Dodekaeder, Ikosaeder),
• Prismen und Antiprismen,
• die archimedischen Körper.

Archimedische Körper

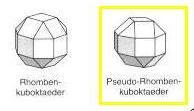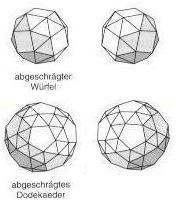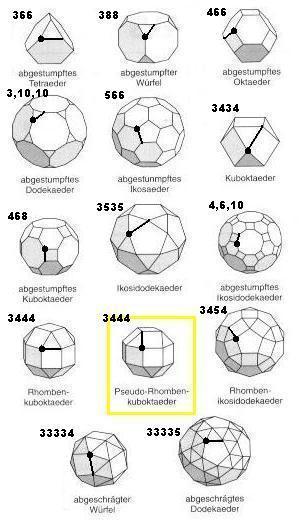
Ausgehend von der markierten Kante erhält man bei Drehung gegen den Uhrzeigersinn die angegebene Folge von Vielecken.		Charakteristiken (3,3,3,3,3) Ikosaeder (3,3,3,3,4) =1 (3,3,3,3,5) =2 (3,3,3) Tetraeder (3,4,4) Dreiecksäule (3,6,6) =3 (3,8,8) =4 (3,10,10) =5 (5,5,5) Dodekaeder (5,4,4) Fünfecksäule (5,6,6) =6 (4,4,n) n-Eck-Säule (mit (4,4,4) Würfel) (4,6,6) =7 (4,6,8) =8 (4,6,10) =9 (3,3,3,n) Antiprismen (mit (3,3,3,3) Oktaeder) (3,4,3,4) =10 (3,4,4,4) =11 und 11' (3,4,5,4) =12 (3,5,3,5) =13
		Achtung: Zur Charakteristik (3,4,4,4) gibt es zwei nicht kongruente Archimedische Körper (dies wurde erst 1934 von C.P. Miller bemerkt). Verlangt man zusätzlich, dass die Drehgruppe transitiv auf den Ecken operiert, so fällt das Pseudo-Rhomben-Kuboktaeder weg!)
		Der abgeschrägte Würfel und das abgeschrägte Dodekaeder kommen in zwei spiegelbildlichen Varianten vor, die sich nicht durch Drehungen zur Deckung bringen lassen.