Auslander-Reiten-Theorie
Sei Λ eine endlich-dimensionale Algebra.mod Λ ist die Kategorie der (endl.dim.) Darstellungen von Λ.
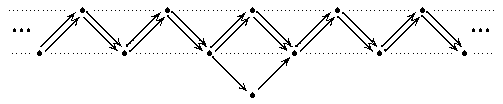
Man konstruiert den Auslander-Reiten-Köcher Γ(Λ),
dies ist ein "Köcher", also ein gerichteter Graph:
- Die Ecken von Γ(Λ) sind die Isomorphie-Klassen
der unzerlegbaren Darstellungen; - Pfeile stehen für irreduzible Abbildungen.
| mod Λ | 
| Γ(Λ) | 
| k[Γ(Λ)] |
Es zeigt sich:
Die Maschenkategorie k[Γ(Λ)] ist
ein vereinfachtes Modell
der Kategorie mod Λ.

1926 - 1994

1942 -