Das (Newcomb-)Benford-Gesetz

Die Wahrscheinlichkeit w(d) für das Auftreten von d = 1,...,9 als erste Ziffer einer Zahl ist

w(d) = log₁₀(d+1/d) = log₁₀(d+1) - log₁₀(d)

(bei "gleichverteilten" Zahlen).

Frank Benford 1938
Simon Newcomb 1881 (American Journal of Mathematics)

Die Google-Fundstellen der Zahlen d65 mit d = 1,...,9

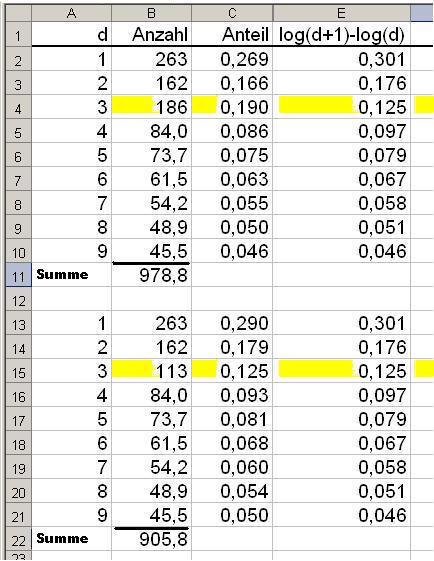
Das Ergebnis für d = 3 ist offensichtlich ein Ausreißer (warum?),
ersetzt man die Fundstellenzahl 186 000 000
durch die kleinere Zahl 113 000 000 (untere Tabelle),
so erhält man eine Zahlenverteilung, die dem Benfordschen Gesetz entspricht.