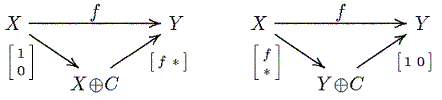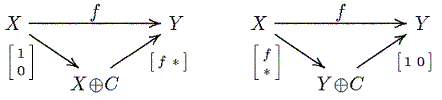An exact sequence 0 → X → Y → Z → 0
is called an Auslander-Reiten sequence
provided the maps
X → Y and Y → Z are irreducible
(as a consequence, X, Z are indecomposable).
The Auslander-Reiten quiver of an exact category is defined as follows:
- Its vertices are the isomorphism classes [X]
of indecomposable objects X
- There is an arrow [X] → [Y], provided
there exists an irreducible map X → Y.
- If 0 → X → Y → Z → 0 is an Auslander-Reiten sequence,
and Yi is an
indecomposable direct summand of Y
then ([X],[Yi],[Z])
is a 2-simplex.