Metric spaces:

A metric on a set X determines

a topology
a completion.

Metrics with the same topology may yield different completions.

Examples:

		R with the usual metric (Euclidean distance) X coincides with its completion.
		The metric of the open interval ]0,1[ The completion is compact, a 2-pont compactification.
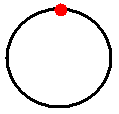
		The metric of S¹-{*}
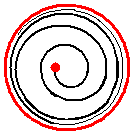
		The metric of the subset {(x,sin(1/x)\| x > 0} The completion adds a whole interval.
		The completion adds a circle and a point.

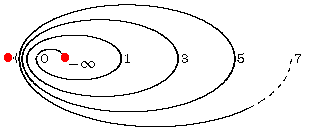
It is of interest to look at non-trivial Cauchy sequences in each case!

A further metric, with just two additional limit points:
one is minus infinite,
the other is the limit of 2N.

Note that all the examples can be modified in order to restrict to Q.
To deal with a countable set with a metric with values in Q, so that the completion is the space exhibited above.