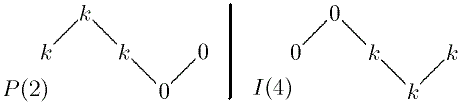
These algebras have been characterized by Tachikawa in 1961 and he exhibited the structure of their indecomposable representations.
Such algebras obviously are of bounded representation type, thus of finite representation type, according to the first Brauer-Thrall conjecture (established by Roiter in 1968).
Hubery (2007): An algebra is of local-colocal representation type if and only if the class of decomposable modules is closed under extensions.
For such an algebra, the decomposable modules yield a subring of its Hall algebra!
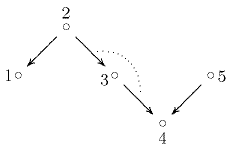
| An example: | 
| Two indecomposable modules which are not serial:
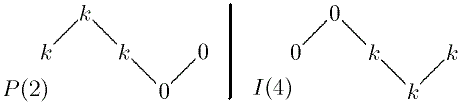
|