1. Der Landschaftspark München Riem im Rundblick: Analyse
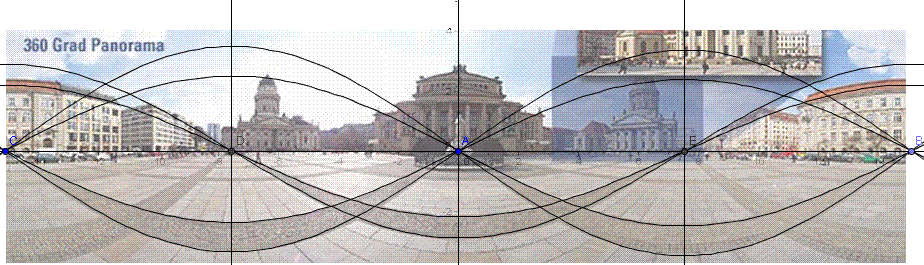
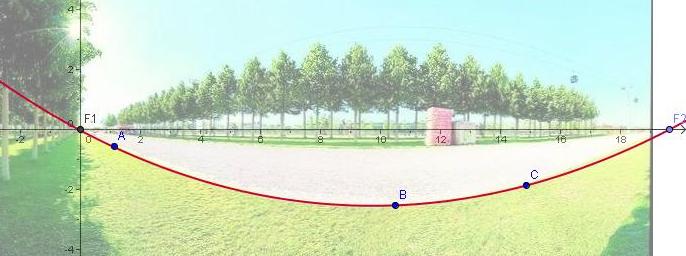
In der letzten Zeit werden in Zeitungen und im Internet immer häufiger Panorama-Fotografien veröffentlicht. Solche Bilder entstehen, indem die Kamera einen vollen Schwenk um 360° durchführt. Genau genommen werden dabei viele kleine senkrechte Streifen aneinander gesetzt, bis der Kreis geschlossen ist. Das Gesamtbild kann man sich als einen abgerollten Zylinder vorstellen. In der Süddeutschen Zeitung fand sich das folgende Panorama-Bild (Abb. 1) vom Landschaftspark Riem in München. Es schreit geradezu danach, die hier sichtbaren Kurven zu untersuchen. Sie erinnern an Parabeln, oder sind es doch eher Teile von Hyperbeln, oder …? Will man dies untersuchen und die zugehörigen Funktionsterme entwickeln, muss man sich zunächst Gedanken machen über die Projektionen, die hier eine Rolle spielen.

Abbildung 1
1.1. Zentralprojektion auf einen Zylinder.
Wie wird ein Punkt P (etwa ein Vogel) bei einer solchen Fotografie auf dem Panorama-Bild (dem abgerollten Zylinder) dargestellt? Zur Untersuchung dieser Frage werden lediglich der 2. Strahlensatz und die Definition des Sinus im rechtwinkligen Dreieck benötigt, dies allerdings im R3. Das sieht dann etwa folgendermaßen aus: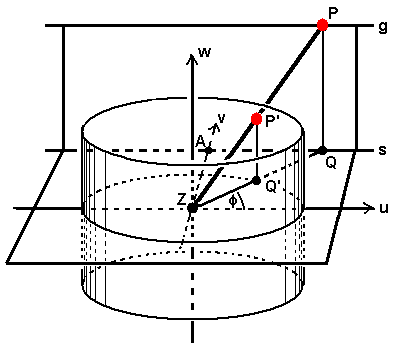
Abbildung 2
Wir verwenden hier für den R3 ein uvw-Koordinatensystem, um im Panorama-Bild mit einem xy-Koordinatensystem arbeiten zu können. Projektionszentrum ist der Ursprung, den wir mit Z bezeichnen werden, projiziert wird auf den Zylinder über dem Einheitskreis. Die uv-Ebene ist also die (waagrechte) Ebene in Augenhöhe, sie entspricht auf dem projizierten Bild der Horizontlinie.
Unser Punkt P (der Vogel) liefert als Bildpunkt den Punkt P' auf dem Zylinder. Als erstes wollen wir die Höhe y von P' über der uv-Ebene bestimmen. Bezeichnen wir mit Q den Fußpunkt der Projektion von P auf die uv-Ebene, so erhalten wir links die Strahlensatzfigur QZP
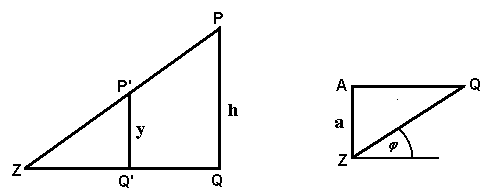
Abbildung 3
Die Länge einer Strecke AB wird im Folgenden mit |AB| bezeichnet; entsprechend ist |ZQ'| = 1. Wir setzen |P'Q'| = y und |PQ| = h. Der zweite Strahlensatz liefert |P'Q'| : |PQ| = |ZQ'| : |ZQ|, also y : h = 1 : |ZQ|, und demnach y = h/|ZQ|.
Wir zeichnen die Parallele s zur u-Achse durch den Punkt Q. Sei a der Abstand der Gerade s vom Ursprung Z (in der Zeichnung ist dies gerade die Länge der Strecke ZA). Wir betrachten nun das Dreieck ZQA. Den Winkel zwischen der x-Achse und der Strecke ZQ haben wir mit φ bezeichnet. Das Dreieck ZQA zeigt, dass |ZQ| = a/sin(φ) gilt. Daher ist
| y = h/|ZQ| = (h/a).sin(φ) |
Das gesuchte Panorama-Bild entsteht, wenn man den Zylinder abrollt: Abgerollt erhält man als xy-Koordinaten des Punkts P' die folgenden beiden Werte: x = -φ (das Minus-Zeichen erhalten wir, da der Drehwinkel φ zwischen der u-Achse und der Strecke ZQ' entgegengesetzt zum Uhrzeigersinn angesetzt wird, im xy-Koordinatensystem des abgerollten Zylinders aber rechtsorientiert gelesen wird), und y ist wie bisher der Abstand von P' von der uv-Ebene, da wir die Horizontlinie auf die x-Achse legen.
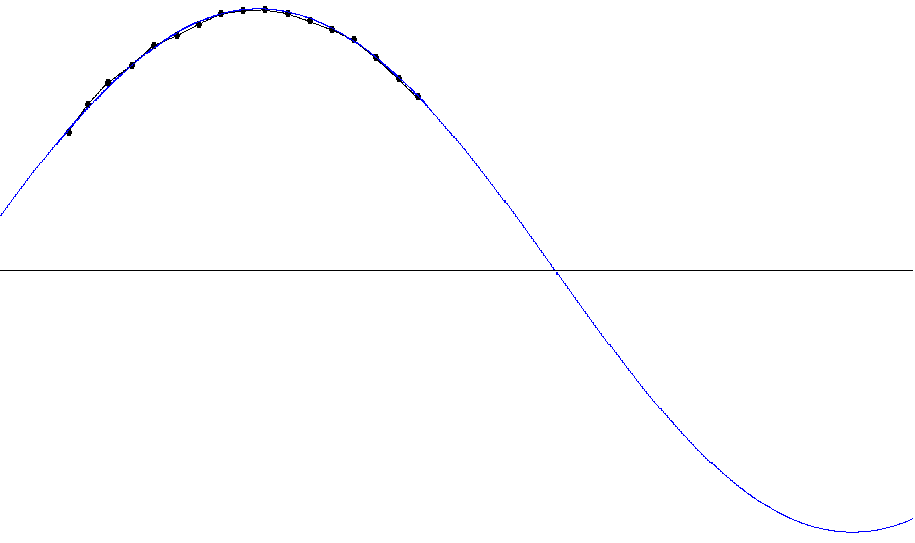
Nehmen wir nun zusätzlich an, dass P auf einer Geraden g liegt, die parallel zur u-Achse verläuft (dann ist s die Vertikalprojektion der Geraden g in die uv-Ebene), so ist klar, dass der Quotient konstant ist: Das Bild der Geraden g auf dem abgerollten Zylinder ist also eine Sinus-Kurve. Wirklich? Nein, wir erhalten nur die Hälfte einer Sinuskurve, nämlich den Bogen mit 0 < φ < π.
Unabhängig von diesen Überlegungen sieht man: Je weiter der Punkt P auf der Geraden g nach außen wandert, umso geringer ist die Höhe y, der Punkt P' liegt dann fast auf dem Einheitskreis. Das entspricht der Erfahrung, dass weit entfernte Objekte (fast) auf der Horizontlinie liegen. Wir haben hier vorausgesetzt, dass die Gerade g zur u-Achse parallel ist. Im Allgemeinen werden wir für eine beliebige horizontale Gerade einen entsprechenden Bogen erhalten, der allerdings entlang der x-Achse verschoben ist.
1.2. Die Sinus-Bögen im Panoramabild des Landschaftsparks Riem.
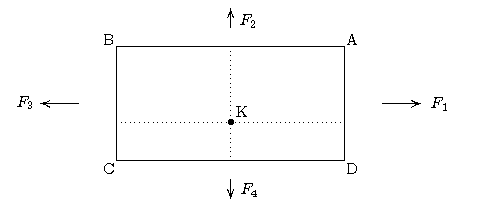
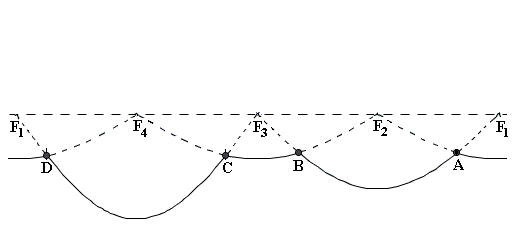
Kehren wir zurück zum Panorama-Bild vom Landschaftspart Riem: rechts sehen wir eine geradlinige Straße: unser Punkt P (hier nun ein Punkt der Straßenkante) liefert beim Schwenk der Kamera einen Bildpunkt P’, der sich sinusförmig bewegt: wir erhalten auf dem Bild die halbe Sinuskurve - die Straße rückt irgendwann ins Blickfeld und verschwindet nach einer Drehung von 180° wieder aus dem Blickfeld.Wir beginnen nun umgekehrt mit dem Panorama-Bild und stellen uns die Aufgabe, einen derartigen Sinus-Bogen effektiv zu beschreiben. Es bietet sich hier an, einen der beiden Fluchtpunkte F1 (an dem die Straße in der Horizontlinie endet) als Ursprung zu wählen, und dann den 2. Fluchtpunkt (die 2. Nullstelle) F2 durch Ablesen anzupeilen, und damit haben wir die Periodenlänge. Neben der Periodenlänge haben wir als zweiten Parameter die Amplitude, also den Quotienten h/a zu bestimmen: auch hier ist man auf Augenmaß und Probieren angewiesen (manchmal werden die Maße von a und h aber auch bekannt sein).
Zusätzlich halten wir Folgendes fest: Alle Parallelen zu unserer Straßenkante erreichen die Horizontlinie in denselben beiden Punkten. Wir erhalten also eine ganze Schar von Sinus-Bögen durch unsere Fluchtpunkte, die parallele Geraden der Realität (Straßenränder, Baumreihen, Schattenränder der Bäume, Baumwipfel) auf dem Foto wiedergeben.
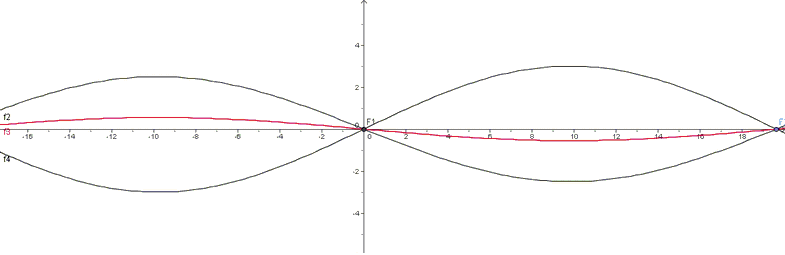
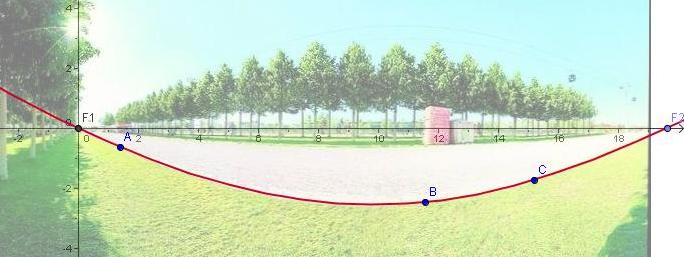
Abbildung 4a

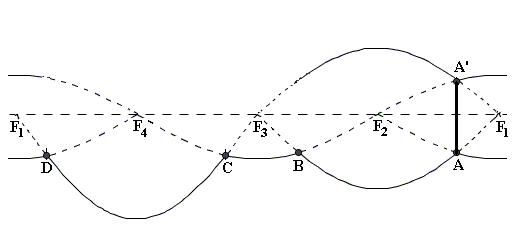
Abbildung 4b
Wir haben oben notiert, dass die x-Achse des Panorama-Bilds den Rechtsschwenk der Kamera beschreibt, im Gegensatz zur üblichen Konvention eines Drehwinkels, der einem Linksschwenk entsprechen würde, dass also x = -φ gesetzt wird. Die Funktionsgleichungen, die sich hier beim Experimentieren ergaben, sind:

Ganz allgemein gilt: Gerade Linien unterhalb der Augenhöhe ergeben einen unteren (also konkaven) Sinus-Bogen, Linien oberhalb entsprechend einen oberen (also konvexen) Sinusbogen.
Noch einige Hinweise zum Panorama-Bild von Riem:
- Die Seilbahn, die am rechten Bildrand recht deutlich zu erkennen ist, verläuft offensichtlich nicht parallel zur Straße, der Fluchtpunkt ist hier ein anderer. Eine Sinuskurve, die ihren Verlauf nachzeichnen würde, gehört deshalb nicht zur betrachteten Schar. (Außerdem ist bei der Seilbahn zu berücksichtigen, dass die Seile sicher keine Gerade bilden, sondern durchhängen.)
- Das Bild musste für die Kurvenanpassung leicht gedreht werden, da offensichtlich die Drehachse der Kamera bei der Aufnahme nicht absolut vertikal ausgerichtet war.
- Das Bild zeigt kein vollständiges Panorama von 360o, wie man an den beiden Fluchtpunkten, die außerhalb des Bildes liegen, erkennen kann. Es fehlen etwa 12o (man beachte, dass das Hintergrundbild in Abbildung 4 b bei den Kurvenanpassungen mit GeoGebra links noch weiter beschnitten wurde).
1.3. Ebene Schnitte eines Zylinders.
Das Problem, mit dem wir uns beschäftigen, lässt sich auch anders beschreiben: wir betrachten hier das Schnittverhalten eines Zylinders mit einer Ebene E. Die Ebene, von der hier die Rede ist, ist die Ursprungs-Ebene durch die Gerade g, auf ihr liegen die Sichtstrahlen zu den Punkten P der Gerade. Nun weiß man aber, dass eine derartige Ebene den Zylinder im Allgemeinen in einer Ellipse schneidet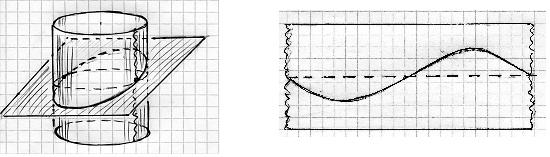
Abbildung 5
Man kann sich die entstehenden Sinuskurven leicht ansehen, wenn man den Pappkern einer Toilettenpapier-Rolle schräg zersägt, den Mantel aufschneidet und die Säge-Kante betrachtet. Eine Wurstpelle, gekonnt abgezogen, tut’s auch.

Abbildung 6
Betont werden sollte, dass die so entstandenen Ellipsen den uv-Einheitskreis in diametral gegenüberliegenden Punkten schneiden, dass wir also im Panorama-Bild immer Sinus-Funktionen erhalten, deren Wendepunkte im Abstand π auf der x-Achse liegen (falls wir mit einem Zylinder mit Radius 1 arbeiten): Da die Ebene E durch den Ursprung geht, schneidet sie die uv-Ebene in einer Ursprungsgeraden, eine Ursprungsgerade schneidet aber den Einheitskreis in diametral entgegengesetzten Punkten. Es gibt einen Ausnahme-Fall: steht die Ebene senkrecht auf der uv-Ebene, so erhält man als Schnitt mit dem Zylinder zwei gegenüberliegende Mantellinien.
1.4. Zusammenfassung: Die Sinusbögen der Panoramabilder.
Wir fassen zusammen: Ausgangspunkt ist wieder das uvw-Koordinatensystem mit dem Zylinder über dem Einheitskreis der uv-Ebene, projiziert werde vom Ursprung Z aus auf diesen Zylinder (Z ist also das wahrnehmende Auge). Das Abrollen des Zylinders liefert unser Panorama-Bild mit einem xy-Koordinatensystem, die x-Achse ist dabei die Horizontlinie (also die Augenhöhe). Ist nun g eine Gerade im Raum, die parallel zur uv-Ebene verläuft und die die w-Achse nicht schneidet, so liefert g unter unserer Projektion einen Sinus-Bogen. Die Sinus-Funktionen, die man auf diese Weise erhält, haben alle die gleiche Frequenz, nämlich, 1/(2π); dagegen sind Amplitude und Phase beliebig: die Funktionen haben die Form2. Geraden im Raum: eine Systematisierung der Möglichkeiten.
2.1. Zentralprojektion von Geraden auf den Zylinder.
Wir wollen nun überblicksartig angeben, welche Möglichkeiten es gibt, eine beliebige Gerade g des R3 auf den Zylinder zu projizieren; der Zylinder habe den Radius 1.Zuerst notieren wir, was passiert, wenn g eine Ursprungsgerade ist:
| Ist g die w-Achse, so erhält man keinen einzigen Projektionspunkt.
| 
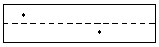
Ist g eine Ursprungsgerade, aber nicht die w-Achse, so erhält man zwei Punkte.
| 
|
Es sei betont, dass sich die x-Koordinaten der beiden Punkte um π unterschieden, und dass die y-Koordinate des einen Punkts das Negative der y-Koordinate des anderen Punkts ist. Derartige Punktepaare spielen eine wichtige Rolle, wir nennen solche Punkte ein entgegengesetztes Punktepaar.
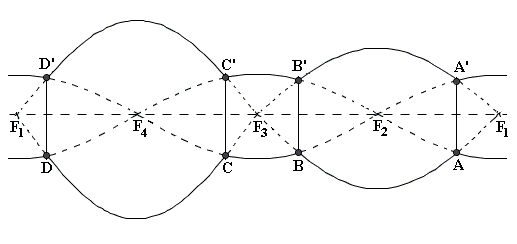
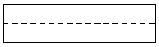
Nun wenden wir uns den Geraden zu, die nicht durch den Ursprung gehen: Von besonderem Interesse sind für uns horizontale und vertikale Geraden, also Geraden, die parallel zur w-Achse, oder parallel zur uv-Ebene sind. Wir bezeichnen mit E die (eindeutig bestimmte) Ursprungsebene, die g enthält. Dabei skizzieren wir jeweils rechts im Panorama-Bild das Bild einer typischen derartigen Geraden g unter der Zentralprojektion (gestrichelt ist die x-Achse eingezeichnet, dies ist gerade die Horizontlinie).
|
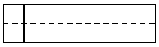
Ist g parallel zur w-Achse, aber verschieden von ihr, so erhält man eine Mantellinie
des Zylinders, also eine senkrechte Gerade im Panorama-Bild.
| 
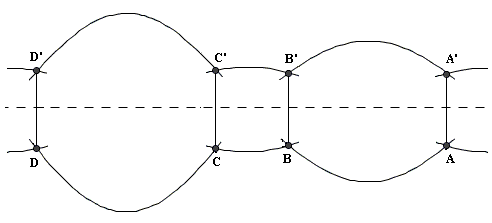
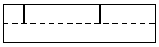
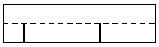
Schneidet g die w-Achse in einem Punkt, aber nicht im Ursprung, und ist sie parallel
zur uv-Ebene, so erhält man zwei gegenüberliegende halbe Mantellinien (dabei ist zu
unterscheiden, ob g oberhalb oder unterhalb der uv-Ebene liegt).
| 
|
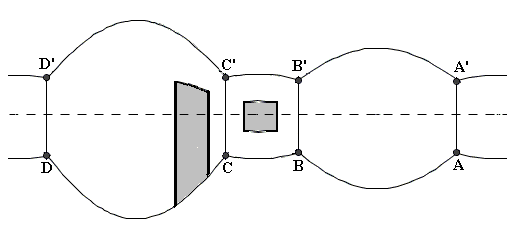
| Ist g eine Gerade in der uv-Ebene, die nicht durch den Ursprung geht, so ist der
Schnitt von E mit dem Zylinder ein Kreis, im Panorama-Bild ist dieser Schnitt die Horizontlinie.
Als Projektionspunkte der Geraden g erhält man auf dem Zylinder einen Halbkreis, also im
Panorama-Bild einen Abschnitt der x-Achse der Länge π.
| 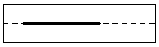
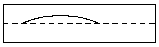
Ist die Gerade g parallel zur uv-Ebene und schneidet sie nicht die w-Achse, so
schneidet E den Zylinder in einer echten Ellipse, im Panorama-Bild ist dieser Schnitt eine
Sinuskurve. Als Projektionspunkte der Geraden g erhält man auf dem Zylinder eine halbe Ellipse,
mit Randpunkten auf dem Einheitskreis. Im Panorama-Bild liefert g einen Sinus-Bogen. (Auch hier
gibt es wieder zwei verschiedene Möglichkeiten, je nach dem, ob g oberhalb oder unterhalb der
uv-Ebene liegt).
| 
|
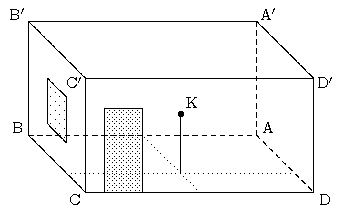
Schließlich notieren wir, was mit einer Geraden g passiert, die weder parallel zur w-Achse, noch parallel zur uv-Ebene ist:
|
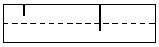
Schneidet g die w-Achse in einem Punkt, aber nicht im Ursprung, und ist sie nicht
parallel zur uv-Ebene, so erhält man zwei gegenüberliegende partielle Mantellinien, die
sich von oben oder unten einem entgegengesetzten Punktepaar nähern (dabei ist zu unterscheiden,
ob der Schnittpunkt von g mit der w-Achse oberhalb oder unterhalb der uv-Ebene liegt).
| 
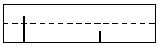
Ist die Gerade g nicht parallel zur uv-Ebene und schneidet sie nicht die w-Achse,
so schneidet E den Zylinder ebenfalls in einer echten Ellipse, im Panorama-Bild ist dieser
Schnitt eine Sinuskurve. Als Projektionspunkte der Geraden g erhält man auf dem Zylinder
eine halbe Ellipse. Die Randpunkte liegen nicht mehr auf dem Einheitskreis. Im Panorama-Bild
liefert g einen Ausschnitt der Sinus-Kurve über einem Intervall der Länge π. Die Randpunkte
sind ein entgegengesetztes Punktepaar.
| 
|