Die endlichen Bewegungsgruppen des R³

Bewegungen: Drehungen, Translationen,... (und deren Hintereinanderschaltungen)
abstandserhaltend, orientierungserhaltend (also keine Spiegelungen!)

• In G kann es keine Translationen geben.
• Es gibt einen Fixpunkt 0 für alle g in G ("Schwerpunkt")
  (Nimmt man ihn als Ursprung eines Koordinatensystems, so wird jedes g in G durch eine orthogonale Matrix beschrieben.)
  Insbesondere gilt: Jedes g in G ist eine Drehung mit einer Achse A(g), die durch 0 geht.

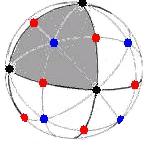
  Für jedes g ≠ 1 in G markieren wir die Schnittpunkte der Achse A(g) mit der Einheits-Sphäre S²: dies liefert zwei "Pole" auf der Einheits-Sphäre S².

Beispiel: Für die Drehgruppe G eines Oktaeders erhalten wir die folgenden Pole: Die Drehachsen durch die Ecken liefern die schwarzen Punkte. Die durch die Kantenmittelpunkte liefern die roten Punkte. Die durch die Flächenmittelpunkte liefern die blauen Punkte.