Einschub: Wurzel-Systeme
(Das Kuboktaeder ist das "Wurzelsystem" vom Typ A3).
Wurzelsysteme spielen in der Mathematik (und der mathematischen Physik)
eine ganz wesentliche Rolle:
- Klassifikation der halbeinfachen Lie-Algebren, der algebraischen Gruppen,
- vieler anderer Strukturen.
- Die Klassifikation der Elementarteilchen basiert auf der
Darstellungstheorie der halbeinfachen Lie-Algebren.
Ein Wurzel-System W ist eine endliche Menge von Vektoren eines euklidschen Vektorraums mit
folgender wesentlichen Eigenschaft:
Seien w, w' in W. Spiegelt man w'
an der zu w orthogonalen Hyperebene,
so ist das Bild w" wieder in W und der Vektor w"-w' ist
ganzzahliges Vielfaches von w.
Beispiele: In der Ebene gibt es nur die folgenden Wurzel-System:
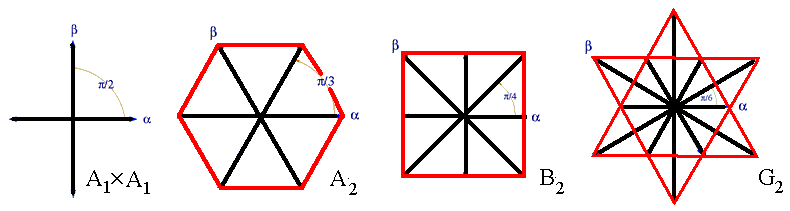
Insgesamt werden die irreduziblen Wurzel-Systeme durch die Dynkin-Diagramme
An, Bn, Cn, Dn, E6, E7,
E8, F4, G2 klassifiziert ...

