Pell'sche Gleichung

Differenzen von Quadraten

Dies wäre einen eigenen Vortrag wert! Ich muss mich daher kurz fassen. Dies ist also eher ein Einschub!

Vom Gnomon war oben die Rede, dieser Begriff wird im übertragenen Sinn auch für folgende L-förmige Figur verwandt:

also für die Differenz zweier Quadrate - da derartige Formen als Zeiger von Sonnenuhren Verwendung fanden.
Wie konstruiert man das geometrische Mittel zweier Zahlen a,b? Gesucht ist also x mit a : x = x : b, also x mit x² = ab. Man bildet das Produkt ab, schreibt es als Differenz zweier Quadrate, nämlich ab = ((a+b)/2)² - ((a-b)/2)²

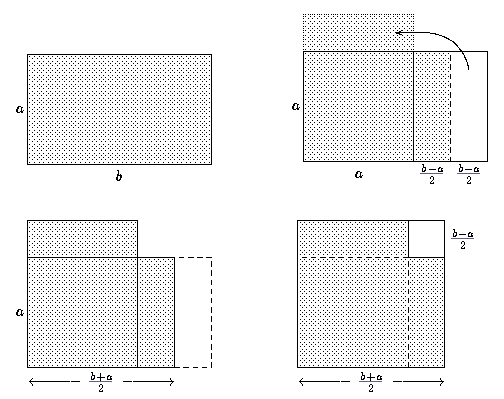
und verwendet nun Pythagoras, um aus der Differenz zweier Quadratzahlen die Wurzel zu ziehen.
Statt von einer Quadratzahl x² eine andere Quadratzahl y² nur einmal abzuziehen, betrachten wir nun allgemeiner Differenzen der Form x² - dy². Frage: welche Zahlen lassen sich so darstellen? Insbesondere: Wann lässt sich die 1 so darstellen?

Die Pell'sche Gleichung

Dies ist die Pell'sche Gleichung: x² - dy² = 1, dabei sei d eine natürliche Zahl und keine Quadratzahl.

Einige Namen

John Pell (1610-1685) nach ihm ist die Gleichung benannt - er hat aber damit nichts zu tun!
Leonhard Euler (1707-1783): er hat den Namen eingefürt, verwechselte aber Pell mit einem anderen Mathematiker, der aber auch nicht viel zur Theorie beitrug...
Joseph Louis Lagrange (1736-1813) zeigte 1768, dass die Pell'sche Gleichung unendlich viele Lösungen besitzt.
Archimedes (287-212 v.u.Z.): auf ihn soll noch eingegangen werden!
Diophantus (um 250 u.Z.) untersuchte ähnliche Fragestellungen
Brahmagupta (598-670) schrieb 628 das Buch Brahmasphutasiddhanta, in dem er viele Pell'sche Gleichungen analysierte.
Bhaskara II (1114-1191) beschrieb als erster eine allgemeine Methode ur Lösung der Pell'schen Gleichung (ohne Beweis - den Beweis führte Lagrange).

Zur Theorie:

Satz: Ist (x,y) eine Lösung der Pell'schen Gleichung x² - dy² = 1, und schreiben wir (x+y√d)ⁿ = x_n+y_n√d, so ist auch (x_n,y_n) eine Lösung.

Einfach zu verfizieren, wenn man mit quadratischen Körper-Erweiterungen vertraut ist; schon Brahmagupta kannte dies!

Auf diese Weise erhält man aus der Gleichung 15² - 14.4² = 1, die folgenden Lösungen der Pell'schen Gleichung für d = 14:

n x² y²
1 15 4
2 449 120
3 13455 3596
4 403201 107760
5 12082575 3229204

Von Brahmagupta stammt der Satz: Wer innerhalb eines Jahres ein Lösungspaar (natürlicher Zahlen) der Gleichung x² - 92y² = 1 findet, ist ein Mathematiker.

Das Rinder-Problem des Archimedes

Es führt auf die Pell'sche Gleichung mit d = 410 286 423 278 424.

Der Sonnengott hat Rinder: weiße, schwarze, gescheckte und braune. Und natürlich Stiere und Kühe. Die Anzahlen sollen wie folgt bezeichnet werden:

Farbe weiß schwarz gescheckt braun
Stiere x y z t
Kühe x' y' z' t'

Hier die Gleichungen, die erfüllt sein sollen:

Die ersten Bedingungen:
x = (1/2+1/3)y+t
y = (1/4+1/5)z+t
z = (1/6+1/7)x+t

Die zweiten Bedingungen:

x' = (1/3+1/4)(y+y')
y' = (1/4+1/5)(z+z')
z' = (1/5+1/6)(t+t')
t' = (1/6+1/7)(x+x')

Als Lösungen der ersten drei Gleichungen erhält man

(x,y,z,t) = m(2226,1602,1580,891),

dabei ist m eine natürliche Zahl.

Die nächsten Gleichungen sind (nur dann) ganzzahlig lösbar, falls m durch 4657 teilbar ist. Sei also m = 4657.k mit einer natürlichen Zahl k, dann ist

(x',y',z',t') = k(7206360,4893246,3515820,5439213).

Die dritten Bedingungen: x+y und 8(z+t)+1 sind Quadratzahlen

Ist x+y Quadratzahl, so ist k = a.l² mit a = 3.11.29.4657.

Ist 8(z+t)+1 = h², so erhalten wir die Gleichung

h² = 8(z+t)+1 = 8.4657.2471.a.l² + 1,

also ist (h,l) eine Lösung der Pell'schen Gleichung für d = 8.4657.2471.a = 2.3.7.11.29.353.2².4657² = 410 286 423 278 424

Diese Pell'sche Gleichung wurde 1880 von A.Amthor gelöst:
Die Gesamtzahl der Rinder ist eine Zahl mit 206545 Ziffern, diemit 7760... beginnt... (1980/1 wurde die Zahl auf 47 Seiten ausgedruckt).

Es gibt aber dennoch Möglichkeiten, die gesuchten Zahlen exakt zu notieren. Hier eine Formel von Lenstra: