Möbius-Bänder im Kubohemioktaeder
|
|
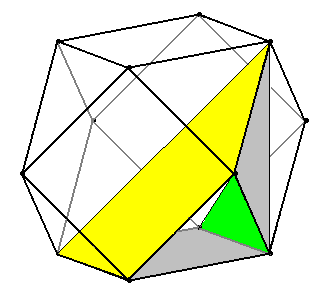
Wir verwenden
- zwei Secksecke
- GELB: Von einem Sechseck brauchen wir drei benachbarte Kanten
(also reicht das
zugehörige halbe Seckseck).
- GRÜN; vom zweiten Sechseck brauchen wir zwei benachbarte Kanten (also reicht das zugehörige
Dreieck).
- zwei Quadrate
- von einem brauchen wir zwei gegenüberliegende Kanten (also das
ganze Quadrat Q): das GRAUE QUADRAT unten.
- von zweiten nur zwei banachbarte Kanten (also reicht das zugehörige
Dreieck D): das GRAUE DREIECK rechts.
|
Es gibt genau 48 derartige Möbius-Bänder:
Zu jedem Paar bestehend aus einem Quadrat Q und einem halben Quadrat D, wobei
der Durchschnitt P von Q und D eine spitze Ecke von D ist,
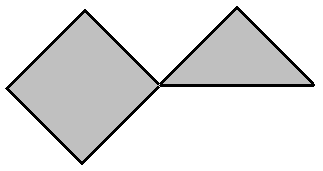
erhält man ein
derartiges Möbius-Band.
(6 mögliche Quadrate, vier Möglichkeiten für P, dann noch zwei
für D.)
Hier noch eine andere Sicht dieses Möbius-Bands: Jede Kantenrichtung
liefert ein Paar von Sechsecken (diese beiden Sechsecken enthalten alle vier Kanten
mit der gegebenen Richtung und sie schneiden sich in einer Geraden mit dieser
Richtung):
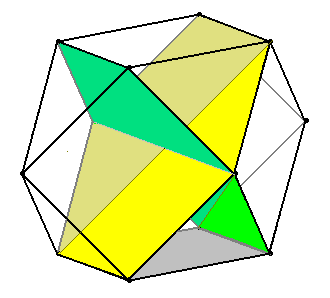
Das Hinzufügen eines halben Quadrats liefert jeweils ein
Möbius-Band (dabei kann man die Secksecke so weit beschneiden, dass die
Schnittgerade wegfällt).
Es gibt 12 Kantenrichtungen, also sechs Konfigurationen der Form
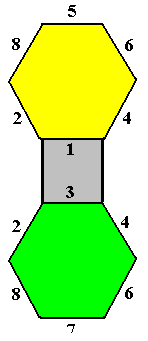
und jeweils können vier halbe Quadrate verwendet werden.
Dritte Indizierung: Es gibt genau 48 Paare (P,k), wobei k eine Kante und P
Eckpunkt auf dieser Kantre ist. Diesen Paaren kann man bijektiv Möbius-Bänder zuordnen.



