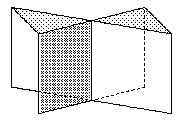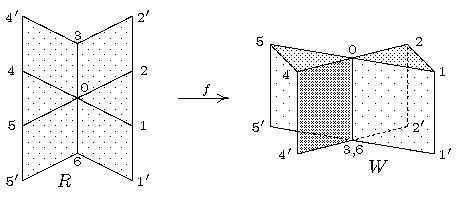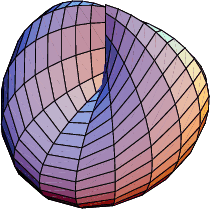
| Dies ist die Fläche N1. | 
|
Wir beginnen mit einem Oktaeder mit den Ecken 0,1,2,3,4,5 und den Dreiecken 012, 023, 034, 041, 125, 235, 345, 045. Wähle 4 paarweise nicht benachbarte Dreiecke; zum Beispiel 012, 034, 235, 145.
Nun fügen wir vier Quadratflächen hinzu; das erste habe die Kanten 10,03,35,51; das zweite habe die Kanten
20,04,45,52; das dritte die Kanten
12,23,34,45.
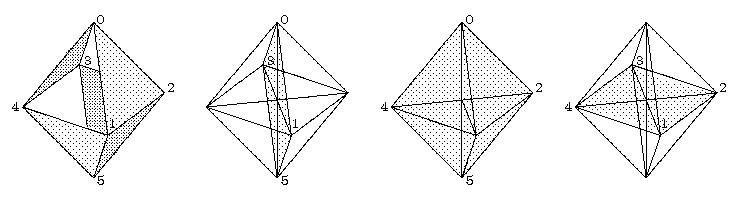
Bei der üblichen Realisierung des Oktaeders im R3
(mit Ecken auf den Koordinatenachsen)
sind die Durchdringungen der Quadratflächen (entlang der Koordinatenachsen) wegzudenken.
(Bemerkungen: "Hepta" = 7, also Heptaeder = Siebenflächner". Das Heptaeder hat, wie das Oktaeder, 12 Kanten und 6 Ecken.

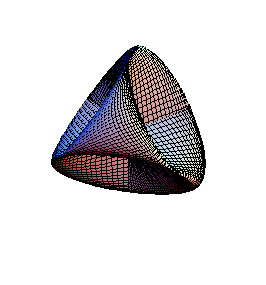
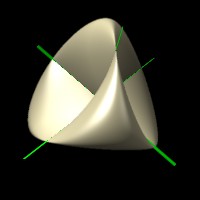
Siehe auch:
Animation der Steiner'schen Römer-Fläche
(Animation von M. R. Sudduth, University of Texas at Arlington)
Hilbert vermutete, dass es keine Immersion der Fläche N1
in den 3-dimensionalen Raum R3 geben könne.
Sein Schüler Werner Boy sollte dies in seiner Dissertaion zeigen -
das Ergebnis war ein anderes: Boy konstruierte eine Immersion, die
sogenannte Boy'sche Fläche. Ein Modell davon steht auf dem Rasen
zwischen den Gebäuden in Oberwolfach:


Siehe auch:
Whitney's Regenschirm (Animation)
(Aus Eric Weisstein's world of Mathematics))