Archimedische Körper

Ein konvexes Polyeder heißt archimedischer Körper, wenn alle Flächen regelmäßige Vielecke sind und alle Ecken die gleiche Charakteristik haben (die Charakteristik ist eine zyklische Folge von Vielecken).

Charakteristiken

(3,3,3,3,3) Ikosaeder
(3,3,3,3,4) =1
(3,3,3,3,5) =2
(3,3,3) Tetraeder
(3,4,4) Dreiecksäule
(3,6,6) =3
(3,8,8) =4
(3,10,10) =5
(5,5,5) Dodekaeder
(5,4,4) Füfecksäule
(5,6,6) =6
(4,4,n) n-Eck-Säule
(4,6,6) =7
(4,6,8) =8
(4,6,10) =9
(3,3,3,n) Antiprismen
(3,4,3,4) =10
(3,4,4,4) =11
(3,4,5,4) =12
(3,5,3,5) =13

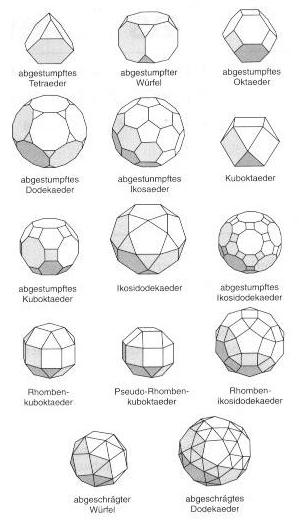
Achtung: Zur Charakteristik (3,4,4,4) gibt es zwei nicht kongruente Archimedische Körper (dies wurde erst 1934 von C.P. Miller bemerkt). Verlangt man zusätzlich, dass die Drehgruppe transitiv auf den Ecken operiert, so fällt das Pseudo-Rhomben-Kuboktaever weg!

Der abgeschrägte Würfel und das abgeschrägte Dodekaeder kommen in zwei spiegelbildlichen Varianten vor, die sich nicht durch Drehungen zur Deckung bringen lassen.

Interaktives Abstumpfen und Ausstülpen platonischer Körper.