Gitter
Gitter-Kugelpackungen
Versucht man, mit gleichgroßen Kugeln (sagen wir: Kugeln mit
Radius 1) den Raum R3 auszufüllen, so muss
man sich die einzelnen Mittelpunkte notieren. Dies kann viel
Aufwand bedeuten - ist aber dann einfach, wenn die Menge der
Mittelpunkte ein "Gitter" bildet: Unter einem Gitter versteht man
die Menge der Punkte, die sich als ganzzahlige Linearkombinationen
von drei linear unabhängigen Vektoren a, b, c schreiben lassen
(dann braucht man sich nur die Vektoren a, b, c zu merken).
Zum Beispiel: Die kubische Kugelpackung
(Kepler-Packung)
|
|
| |
Hier ein größerer Ausschnitt des Gitters:
|
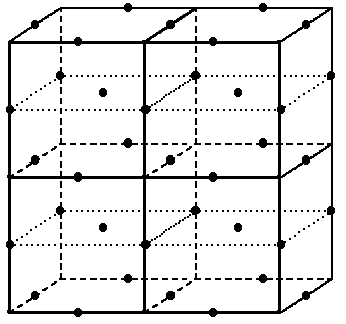
Einsicht: Die kubische Kugelpackung ist hexagonal!
|
|
Hier ein Puzzle,
das mit den verschiedenen Ebenen
im Gitter spielt:
"Der verschwundene Raum":
5 Kugelkombinationen mit insgesamt 14 Kugeln sind so in den
Kubus zu legen, dass alle Platz finden. Mit 13 Kugeln
geht es aber auch, wo ist also der Platz für die 14. Kugel
geblieben?
| 
http://www.f-brunner.ch/
|
(Coffin/Botermans)
|
|
Ganz allgemein kann man am Gitteraufbau ablesen, wie bei
Kugel-Puzzles einzelne Teile liegen können. Hier einige
Möglichkeiten
für die rechtwinkligen Dreier
| und für die Metallstangen
beim
"Fluch des Pharao"
von Markus Götz
| 
| |
Wie sitzt eine Dreieckspyramide in diesem Gitter?
Die Schnitte mit horizontalen Ebenen sind in verschiedenen
Farben markiert: Wie erhalten gerade das erste Dreieckspyramiden-Puzzle.
Hier das kompliziertere Dreieckspyramiden-Puzzle (mit den Steinen
4,3,2,L,T,V):
