Hex

III. VERSCHRÄNKUNG

Das Nebeneinander der Quadratwelt und der Dreieckswelt ist zu hinterfragen -
die beiden Welten sind aufeinander bezogen!

Man nehme einen Würfel, mit Eckpunkten 1 bis 8
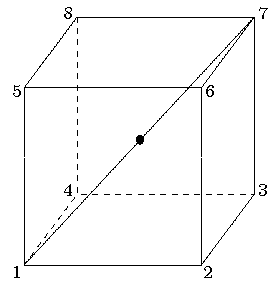
(unten zum Beispiel 1 2 3 4, darüber jeweils 5 6 7 8),
und betrachte eine Raumdiagonale, etwa 1 7.
Man schneide den Würfel senkrecht zur Raumdiagonale,
und zwar durch den Mittelpunkt der Raumdiagonale.
Was erhält man?
Ein Dreieck? ein Viereck? ein Fünfeck?

Irreführend ist: die Schnittebene ist eine schräge Ebene!
Man stelle den Würfel auf eine Ecke: Die Raumdiagonale ist nun senkrecht, die Schnittebene ist waagrecht.
Jetzt ist alles viel einfacher: Man sieht
Symmetrien: Rotation um 120^o.
Oder auch: direkt über der Schnittebene gibt es drei Ecken, direkt unter ihr gibt es ebenfalls drei Ecken...

Nächste Frage:

Wie gross ist denn dieses Seckseck?
Kantenlänge?
Flächeninhalt?

Genauer:

Schneiden wir durch die Nachbarecken der Spitze: wir erhalten ein Dreieck
Schneiden wir in der Mitte: wir erhalten ein Seckeck
Schneiden wir durch die Nachbarecken der Spitze: wir erhalten ein Dreieck

Zusatz: Ist das Sechseck Durchschnitt dieser Dreiecke?
Also wie beim Wurzelsystem G2 ?

Zwischenfrage:

Wie gross ist denn das Seckseck?
Kantenlänge?
Flächeninhalt?
(Ausgangspunkt: Würfel mit Kantenlänge 1)

Kantenlänge? 1/2 mal Wurzel aus 2
Kantenlänge der Dreiecke: Wurzel aus 2.
Kantenlänge des Durchschnitts-Sechsecks: 1/3 mal Wurzel aus 2.
(Kantenlänge der konvexen Hülle: 1/3 mal Wurzel aus 6)

Einfachste Konstruktion des Seckecks: als Mitten-Sechseck der konvexen Hülle.

Vortrag 1998

Zentralabitur-Aufgabe 2007
Aufgabe (Bruder?): Gesucht ein Netz, sodass die Kanten des Schnitt-Sechsecks auf einer Geraden liegen.

		Irreführend ist: die Schnittebene ist eine schräge Ebene!
		Man stelle den Würfel auf eine Ecke: Die Raumdiagonale ist nun senkrecht, die Schnittebene ist waagrecht. Jetzt ist alles viel einfacher: Man sieht Symmetrien: Rotation um 120^o. Oder auch: direkt über der Schnittebene gibt es drei Ecken, direkt unter ihr gibt es ebenfalls drei Ecken...