Reguläre Polyeder
- Die Flächenstücke sind reguläre kongruente (ebene) Polygone
- Jede Kante gehört zu genau zwei Flächenstücken.
- Alle Ecken sind kongruent.
- Die Fläche ist zusammenhängend.

Reguläre Polyeder
| 
|
| e | k | f | χ(F) | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | das große Dodekaeder | | 2 | das große Ikosaeder
| 3 | das große Stern-Dodekaeder
| 4 | das kleine Stern-Dodekaeder
| | |||||||||||||||||||||||
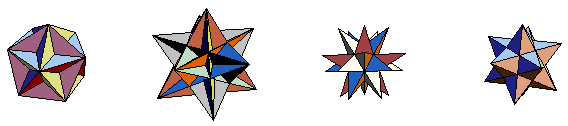 Das große Ikosaeder und das große Stern-Dodekaeder sind beides
nichts anderes als 2-Sphären ("durcheinandergewurschtelt"); beim
großen Dodekaeder und beim kleinen Stern-Dodekaeder dagegen handelt es sich
um die Fläche F4 (ebenfalls "durcheinandergewurschtelt"):
Das große Ikosaeder und das große Stern-Dodekaeder sind beides
nichts anderes als 2-Sphären ("durcheinandergewurschtelt"); beim
großen Dodekaeder und beim kleinen Stern-Dodekaeder dagegen handelt es sich
um die Fläche F4 (ebenfalls "durcheinandergewurschtelt"):
