S³ als Vereinigungsmenge zweier Voll-Tori

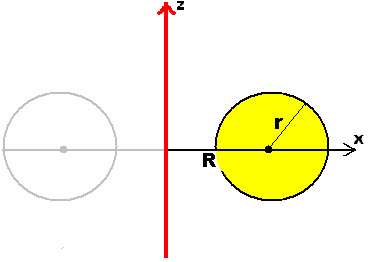
Ein Torus entsteht durch Rotation eines Kreises, entsprechend entsteht ein Voll-Torus durch Rotation einer Kreisscheibe. Man nimmt also alle Punkte im "Innern" des Torus hinzu.

Wie sieht der Außenbereich aus? Nimmt man den Punkt ∞ hinzu, so ist der Außenbereich ebenfalls ein Voll-Torus.

Man kann also S3 als Vereinigung zweier Tori auffassen, die sich genau an ihren Rändern überlappen. Man nennt dies die Clifford-Zerlegung der S3 in zwei Tori. Clifford-Torus im R4 = C2: die Menge der (x,y,z,t) mit x2+y2 = 1 = z2+t2.

William Clifford (1845-1879)