Fibonacci (rechts)                       (und Fahr, links)

Leonardo Pisano, called Fibonacci, was born in Pisa (probaly in 1170) but was educated in North Africa where his father held a diplomatic post. Fibonacci was taught mathematics in Bugia and travelled widely with his father and recognised the enormous advantages of the mathematical systems used in the countries they visited.

Fibonacci ended his travels around the year 1200 and at that time he returned to Pisa. There he wrote a number of important texts which played an important role in reviving ancient mathematical skills and he made significant contributions of his own. In particular, he writes the famous Liber abaci (1202) The book was based on the arithmetic and algebra that Fibonacci had accumulated during his travels. The book, which went on to be widely copied and imitated, introduced the Hindu-Arabic place-valued decimal system and the use of Arabic numerals into Europe. Certainly many of the problems that Fibonacci considers in Liber abaci were similar to those appearing in Arab sources.

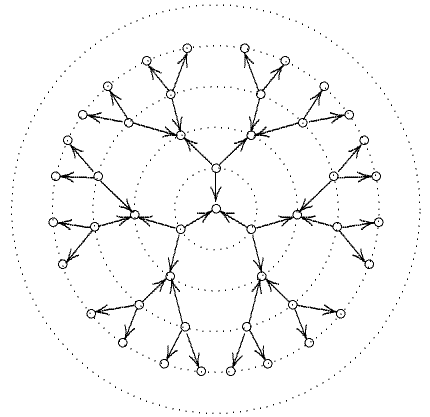
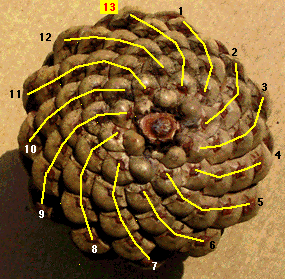
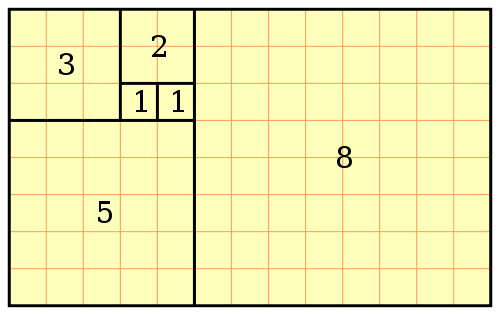
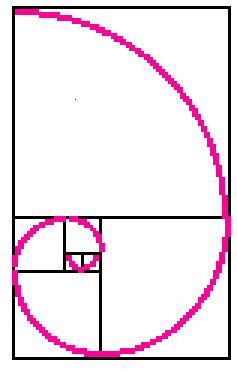
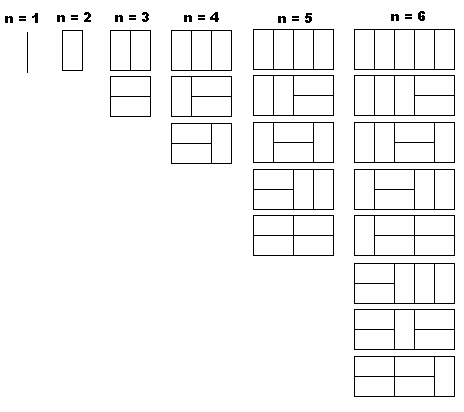
The second section of Liber abaci contains a large collection of problems aimed at merchants. They relate to the price of goods, how to calculate profit on transactions, how to convert between the various currencies in use in Mediterranean countries, and problems which had originated in China. One might have thought that at a time when Europe was little interested in scholarship, Fibonacci would have been largely ignored. This, however, is not so and widespread interest in his work undoubtedly contributed strongly to his importance, although it was the practical applications rather than the abstract theorems that made him famous to his contemporaries. A problem in the third section of Liber abaci led to the introduction of the Fibonacci numbers and the Fibonacci sequence for which Fibonacci is best remembered today: A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?

Das Wachstums-Modell einer Kaninchen-Population:
die Zahlenfolge 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Phyllotaxis: Die Spiralen eines Kiefern-Zapfen

Spiralen aus Quadraten

1-2-Folgen, und Rechtecksparkettierungen

• die Anzahl der Folgen aus Einsen und Zweien mit vorgegebener Summe.
• die Anzahl der möglichen Folgen von Einzel- und Doppelhäusern
• die Anzahl der Parkettierungen eines 2×(n-1)-Rechtecks durch Dominoes
  

Wir wünschen Euch viele Fibonacci-Folgen!

-

Was aber die Fibonacci-Zahlen wirklich mit dem Glücksrad zu zun haben, wird hier nicht verraten
(Mathematik ist eben eine Geheimwissenschaft.)