Copy of my home page at IAS in the Academic Year 1999-2000.
Original URL of this page:
http://www.math.ias.edu/~rost
Lectures on Norm Varieties
![[image: colored graphic of triality, designed by H. Rost]](images/triality.jpg)
Welcome to Markus Rost's home page at the Institute for Advanced
Study.
I am Member of the School of
Mathematics at IAS for the
Academic Year 1999/2000, participating in the Motivic Homotopy
Theory Program. For more informations about me see my regular home
page.
This page contains informations about the "Lectures on Norm
Varieties", a series of talks held at IAS during the winter term
1999 and the spring term 2000.
The lectures take place weekly in the Math building on
Wednesdays, room M-101, 2:00 pm. First lecture on
Oct. 6, no lecture on Nov. 24, last lecture in 1999 on Dec. 8. To be
continued on Jan. 19, 2000. No lectures on March 15, March 22.
Additional lecture on Friday, March 31, 2:00 pm;
further on Friday, April 7, 2:00 pm, West Building Lecture
Hall, on Monday, April 10, 2:00 pm, and on
Tuesday, April 11, 2:00 pm. No lecture on April 12
and thereafter, except for the last three lectures on
Wednesday, May 17, 2:00 pm, Monday, May 22,
2:00 pm, and Wednesday, May 24, 2:00
pm. Check also the announcement of the Mathematics
Seminars.
Related literature can be found below.
Notes are not available.
Here are two little impressions:
An identity in K2
This is an identity in K2 of a field:
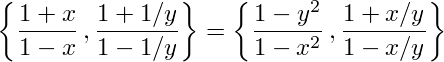
Check it (without using a pencil!) by comparing residues on
K2k(x,y).
For applications of this identity to Galois
cohomology see [Haile et al., 1996].
The fundamental relation in cobordism
Every 1-dimensional closed manifold M is a boundary:
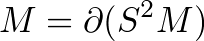
Here S2M denotes the symmetric square (M×M)/(Z/2) of
M.
There is a generalization to higher dimensions: For any closed
manifold M the projective tangent bundle together with its
tautological line bundle is bordant. One may use this observation to
obtain the Wu relations for the Stiefel-Whitney numbers and to compute
the unoriented cobordism ring.
In the following we list some of the literature
related to various topics mentioned in the lectures. Once in a while
the list will be updated, extended, or corrected.
Milnor's K-theory
The basic texts for the definitions of Milnor's K-ring and its norm
are [Milnor, 1970] and [Bass and Tate, 1973].
The well-definedness of the norm was first proven in [Kato, 1980].
A fundamental sum formula ("dd=0") is shown in
[Kato, 1986].
Sections 1 and 2 of [Rost, 1996] contain a summary of the basic
functorial properties of Milnor's K-theory and other modules over
Milnor's K-ring, like Galois cohomology.
For the isomorphism between Milnor's K2 and the
"classical" K2 of a field (Matsumoto's Theorem)
see [Milnor, 1971].
See also Chapter III of [Weibel, 1997].
Galois cohomology
Standard references are Cohomologie Galoisienne [Serre, 1994] and
Corps Locaux [Serre, 1962] (or the translations [Serre, 1997] and
[Serre, 1979]).
See also Chapter VII in The Book of Involutions
[Knus et al., 1998].
Bloch-Kato conjecture
For n=p=2 ("Merkurjev's Theorem"): [Merkurjev, 1981],
[Suslin, 1982], [Wadsworth, 1986], [Arason, 1984].
For n=2 ("Theorem of Merkurjev and Suslin"):
[Merkurjev and Suslin, 1982], [Suslin, 1987].
For n=3, p=2: [Merkurjev and Suslin, 1990a], [Merkurjev and Suslin, 1990b],
[Rost, 1986], [Rost, 1988a].
For p=2 ("Milnor conjecture"): [Voevodsky, 1996].
Central simple algebras
See Chapter I in The Book of Involutions
[Knus et al., 1998] and the literature mentioned
there, in particular [Scharlau, 1985] and [Draxl, 1983].
For symbol algebras (cyclic algebras) see also [Milnor, 1971].
K1 and SK1 of central simple
algebras
For a survey on the Ki of central simple algebras (i=0,1,2)
see [Merkurjev, 1995b].
The first example of a non-trivial SK1 is due to
[Platonov, 1976], see also [Draxl, 1983] and [Suslin, 1991].
The non-triviality of the generic element in SK1 for
algebras with index divisible by 4 has been shown in
[Merkurjev, 1993].
See also Chapter IV in The Book of Involutions
[Knus et al., 1998].
Pfister forms
Standard references for quadratic forms are [Lam, 1980] and
[Scharlau, 1985]. For the relations with Milnor's K-theory see
[Milnor, 1970]. The well-definedness of the homomorphism
en (n=3,4) is established in [Arason, 1975],
[Jacob and Rost, 1989].
Chow groups
For the classical Chow groups see
[Fulton, 1984]. For the groups Ap(X,n) see
[Rost, 1996].
Birational invariance of A0(X)
See Corollary 12.10 in [Rost, 1996]. For unramified cohomology see
the survey [Colliot-Thélène, 1995].
Characteristic numbers
The basic references are [Milnor and Stasheff, 1974] and
[Stong, 1968]. For the Todd numbers and their properties see
[Hirzebruch, 1995]. The denominators of the Todd classes are
computed in [Atiyah and Hirzebruch, 1961]. The Riemann-Roch theorem in
the algebro-geometric setting can be found in [Fulton, 1984].
Steenrod operations
See [Steenrod, 1962], [Milnor, 1958], [Margolis, 1983].
Cobordism and formal group laws
See Quillen's paper [Quillen, 1971] and Adam's Chicago Lectures
[Adams, 1995]. The unoriented cobordism ring is treated in
[Bröcker and tom Dieck, 1970]. Further references: [Thom, 1954],
[Ravenel, 1986], [Shibata, 1971], [Shibata, 1973],
[Buoncristiano and Hacon, 1981], [Buoncristiano and Hacon, 1983],
[Buoncristiano and Hacon, 1985], [Buoncristiano and Hacon, 1986]. For the
formal group law version of the fundamental relation in unoriented
cobordism see [Rost, 2000].
Minimal dimension of generic splitting varieties
For elements in the Brauer group or for Pfister forms see Theorem 4.1
resp. Corollary 8.2 in [Karpenko, 1999]. See also [Vishik, 1998]
A0(X,1) and "Injectivity"
For a Severi-Brauer variety X of a central simple algebra A the
computations CH0(X)=K0A and
A0(X,1)=K1A appeared first in [Panin, 1984]
resp. [Merkurjev and Suslin, 1992].
For a quadric X, the group A0(X,1) has been studied in
[Rost, 1988b]. In the case of a Pfister form the situation is
somewhat simpler, see [Kahn, 1997].
A related theme is the norm principle and the notion of R-equivalence
for algebraic groups; cf. [Gille, 1993], [Merkurjev, 1995a], and
[Chernousov and Merkurjev, 1998]
Cohomological invariants
For definitions and properties of the H3-invariant see
[Serre, 1995], § 31 in The Book of Involutions
[Knus et al., 1998], and
[Esnault et al., 1998]; unfortunately a complete
exposition on its basic properties is still missing. For the
H3-invariant for F4 (or for exceptional Jordan
algebras) see [Rost, 1991], [Petersson and Racine, 1996], and §
40 in The Book of Involutions [Knus et al., 1998].
Conner-Floyd fixed point theorems
The case of (Z/p)2-actions is treated in
[Conner and Floyd, 1964]. For the general case see [Floyd, 1971].
Chain Lemma
For the case of degree 3 algebras see [Petersson and Racine, 1996]
and [Rost, 1999]. The basis for our considerations will be
[Rost, 1998] (Warning: This text is hard to read without
preliminary remarks).
References
- [Adams, 1995]
- J. F. Adams.
Stable homotopy and generalised homology.
University of Chicago Press, Chicago, IL, 1995.
Reprint of the 1974 original. MR 1324104
- [Arason, 1975]
- Jón Kr. Arason.
Cohomologische Invarianten quadratischer Formen.
J. Algebra, 36(3):448-491, 1975. MR 389761
- [Arason, 1984]
- Jón Kr. Arason.
A proof of Merkurjev's theorem.
In C. R. Riehm and I. Hambleton, editors, Quadratic and Hermitian forms
(Hamilton, Ont., 1983), volume 4 of CMS Conf. Proc.,
pages 121-130. Amer. Math. Soc., Providence, R.I., 1984. MR 776449
- [Atiyah and Hirzebruch,
1961]
- M. F. Atiyah and F. Hirzebruch.
Cohomologie-Operationen und charakteristische Klassen.
Math. Z., 77:149-187, 1961. MR 156361
- [Bass and Tate, 1973]
- H. Bass and
J. Tate.
The Milnor ring of a global field.
In H. Bass, editor, Algebraic K-theory, II: ``Classical'' algebraic
K-theory and connections with arithmetic (Proc. Conf., Seattle, Wash.,
Battelle Memorial Inst., 1972), volume 342 of Lecture Notes in
Mathematics, pages 349-446. Springer, Berlin, 1973. MR 442061
- [Bloch et al.,
1986]
- Spencer J. Bloch, R. Keith Dennis, Eric M. Friedlander, and
Michael R. Stein, editors.
Applications of algebraic K-theory to algebraic geometry and number
theory. Part I, II, volume 55 of Contemporary
Mathematics, Providence, R.I., 1986. American Mathematical Society. MR 862626
- [Bröcker and tom Dieck,
1970]
- Theodor Bröcker and Tammo tom Dieck.
Kobordismentheorie.
Springer-Verlag, Berlin, 1970.
Lecture Notes in Mathematics, Vol. 178. MR 275446
- [Buoncristiano and Hacon,
1981]
- Sandro Buoncristiano and Derek Hacon.
An elementary geometric proof of two theorems of Thom.
Topology, 20(1):97-99, 1981. MR 592572
- [Buoncristiano and Hacon,
1983]
- Sandro Buoncristiano and Derek Hacon.
The geometry of Chern numbers.
Ann. of Math. (2), 118(1):1-7, 1983. MR 707157 [ORIGINAL ARTICLE]
- [Buoncristiano and Hacon,
1985]
- Sandro Buoncristiano and Derek Hacon.
A geometrical approach to characteristic numbers.
In Geometry today (Rome, 1984), pages 21-38. Birkhäuser Boston,
Boston, MA, 1985.
Edited and with a preface by E. Arbarello, C. Procesi and E. Strickland. MR 895144
- [Buoncristiano and Hacon,
1986]
- Sandro Buoncristiano and Derek Hacon.
On the formal groups approach to cobordism.
Proc. Amer. Math. Soc., 97(3):559-564, 1986. MR 840646 [ORIGINAL ARTICLE]
- [Chernousov and Merkurjev,
1998]
- V. Chernousov and A. Merkurjev.
R-equivalence and special unitary groups.
J. Algebra, 209(1):175-198, 1998. MR 1652122
- [Colliot-Thélène, 1995]
- J.-L.
Colliot-Thélène.
Birational invariants, purity and the Gersten conjecture.
In Jacob and Rosenberg [Jacob and Rosenberg, 1995], pages 1-64. MR 1327280
- [Conner and Floyd, 1964]
- P. E. Conner
and E. E. Floyd.
Differentiable periodic maps.
Academic Press Inc., Publishers, New York, 1964.
Ergebnisse der Mathematik und ihrer Grenzgebiete, N. F., Band 33. MR 176478
- [Draxl, 1983]
- P. K. Draxl.
Skew fields, volume 81 of London Mathematical Society
Lecture Note Series.
Cambridge University Press, Cambridge, 1983. MR 696937
- [Esnault et al.,
1998]
- Hélène Esnault, Bruno Kahn, Marc Levine, and Eckart
Viehweg.
The Arason invariant and mod 2 algebraic cycles.
J. Amer. Math. Soc., 11(1):73-118, 1998. MR 1460391 [ORIGINAL ARTICLE]
- [Floyd, 1971]
- E. E. Floyd.
Actions of (Zp)k without stationary points.
Topology, 10:327-336, 1971. MR 283820
- [Fulton, 1984]
- William Fulton.
Intersection theory, volume 2 of Ergebnisse der Mathematik
und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas
(3)].
Springer-Verlag, Berlin, 1984. MR 732620
- [Gille, 1993]
- Philippe Gille.
R-équivalence et principe de norme en cohomologie galoisienne.
C. R. Acad. Sci. Paris Sér. I Math., 316(4):315-320, 1993. MR 1204296
- [Haile et al.,
1996]
- Darrell E. Haile, Max-Albert Knus, Markus Rost, and
Jean-Pierre Tignol.
Algebras
of odd degree with involution, trace forms and dihedral extensions.
Israel J. Math., 96:part B, 299-340, 1996. MR 1433693
- [Hirzebruch, 1995]
- Friedrich
Hirzebruch.
Topological methods in algebraic geometry.
Classics in Mathematics. Springer-Verlag, Berlin, 1995.
Translated from the German and Appendix One by R. L. E. Schwarzenberger, With a
preface to the third English edition by the author and Schwarzenberger,
Appendix Two by A. Borel, Reprint of the 1978 edition. MR 1335917
- [Jacob and Rosenberg, 1995]
- Bill Jacob
and Alex Rosenberg, editors.
K-theory and algebraic geometry: connections with quadratic forms and
division algebras, volume 58, Part 2 of Proceedings of Symposia
in Pure Mathematics, Providence, RI, 1995. American Mathematical
Society. MR 1327285
- [Jacob and Rost, 1989]
- Bill Jacob and
Markus Rost.
Degree four cohomological invariants for quadratic forms.
Invent. Math., 96(3):551-570, 1989. MR 996554
- [Kahn, 1997]
- Bruno Kahn.
La conjecture de Milnor
(d'après V. Voevodsky).
Astérisque, (245):Exp. No. 834, 5, 379-418, 1997.
Séminaire Bourbaki, Vol. 1996/97. MR 1627119
- [Karpenko, 1999]
- Nikita Karpenko.
On
anisotropy of orthogonal involutions.
To appear in J. Ramanujan Math. Soc., 1999.
- [Kato, 1980]
- Kazuya Kato.
A generalization of local class field theory by using K-groups. II.
J. Fac. Sci. Univ. Tokyo Sect. IA Math., 27(3):603-683, 1980. MR 603953
- [Kato, 1986]
- Kazuya Kato.
Milnor K-theory and the Chow group of zero cycles.
In Bloch et al. [Bloch et al.,
1986], pages
241-253. MR 862638
- [Knus et al.,
1998]
- Max-Albert Knus, Alexander Merkurjev, Markus Rost, and
Jean-Pierre Tignol.
The
book of involutions.
American Mathematical Society, Providence, RI, 1998.
With a preface in French by J. Tits. MR 1632779
- [Lam, 1980]
- T. Y. Lam.
The algebraic theory of quadratic forms.
Benjamin/Cummings Publishing Co. Inc. Advanced Book Program, Reading, Mass.,
1980.
Revised second printing, Mathematics Lecture Note Series. MR 634798
- [Margolis, 1983]
- H. R. Margolis.
Spectra and the Steenrod algebra.
North-Holland Publishing Co., Amsterdam, 1983.
Modules over the Steenrod algebra and the stable homotopy category. MR 738973
- [Merkurjev and Suslin,
1982]
- A. S. Merkurjev and A. A. Suslin.
K-cohomology of Severi-Brauer varieties and the norm residue
homomorphism.
Izv. Akad. Nauk SSSR Ser. Mat., 46(5):1011-1046, 1135-1136,
1982.
[Math. USSR Izv. 21 (1983), 307-340]. MR 675529
- [Merkurjev and Suslin,
1990a]
- A. S. Merkurjev and A. A. Suslin.
Norm residue homomorphism of degree three.
Izv. Akad. Nauk SSSR Ser. Mat., 54(2):339-356, 1990.
[Math. USSR Izv. 36 (1991), no. 2, 349-367], also:
LOMI-preprint (1986). MR 1062517
- [Merkurjev and Suslin,
1990b]
- A. S. Merkurjev and A. A. Suslin.
The group K3 for a field.
Izv. Akad. Nauk SSSR Ser. Mat., 54(3):522-545, 1990.
[Math. USSR Izv. 36 (1991), no. 3, 541-565], also:
LOMI-preprint (1986). MR 1072694
- [Merkurjev and Suslin,
1992]
- A. S. Merkurjev and A. A. Suslin.
The group of K1-zero-cycles on Severi-Brauer varieties.
Nova J. Algebra Geom., 1(3):297-315, 1992. MR 1218356
- [Merkurjev, 1981]
- A. S. Merkurjev.
On the norm residue symbol of degree 2.
Dokl. Akad. Nauk SSSR, 261(3):542-547, 1981.
[Soviet Math. Dokl. 24 (1981), no. 3, (1982), 546-551]. MR 638926
- [Merkurjev, 1993]
- A. S. Merkurjev.
Generic element in SK1 for simple algebras.
K-Theory, 7(1):1-3, 1993. MR 1220421
- [Merkurjev, 1995a]
- A. S. Merkurjev.
The norm principle for algebraic groups.
Algebra i Analiz, 7(2):77-105, 1995.
[St. Petersburg Math. J. 7 (1996), no. 2, 243-264]. MR 1347513
- [Merkurjev, 1995b]
- A. S. Merkurjev.
K-theory of simple algebras.
In Jacob and Rosenberg [Jacob and Rosenberg, 1995], pages 65-83. MR 1327281
- [Milnor and Stasheff,
1974]
- John W. Milnor and James D. Stasheff.
Characteristic classes.
Princeton University Press, Princeton, N. J., 1974.
Annals of Mathematics Studies, No. 76. MR 440554
- [Milnor, 1958]
- John Milnor.
The Steenrod algebra and its dual.
Ann. of Math. (2), 67:150-171, 1958. MR 99653 [ORIGINAL ARTICLE]
- [Milnor, 1970]
- John Milnor.
Algebraic K-theory and quadratic forms.
Invent. Math., 9:318-344, 1970. MR 260844
- [Milnor, 1971]
- John Milnor.
Introduction to algebraic K-theory.
Princeton University Press, Princeton, N.J., 1971.
Annals of Mathematics Studies, No. 72. MR 349811
- [Panin, 1984]
- I. Panin.
Applications of K-theory in algebraic geometry, 1984.
Thesis, LOMI, Leningrad.
- [Petersson and Racine,
1996]
- Holger P. Petersson and Michel L. Racine.
An elementary approach to the Serre-Rost invariant of Albert algebras.
Indag. Math. (N.S.), 7(3):343-365, 1996. MR 1621373
- [Platonov, 1976]
- V. P. Platonov.
The Tannaka-Artin problem, and reduced K-theory.
Izv. Akad. Nauk SSSR Ser. Mat., 40(2):227-261, 469, 1976.
[Math. USSR Izv. 10 (1976), no. 2, 211-243]. MR 407082
- [Quillen, 1971]
- Daniel Quillen.
Elementary proofs of some results of cobordism theory using Steenrod
operations.
Advances in Math., 7:29-56 (1971), 1971. MR 290382
- [Ravenel, 1986]
- Douglas C. Ravenel.
Complex cobordism and stable homotopy groups of spheres.
Academic Press Inc., Orlando, Fla., 1986. MR 860042
- [Rost, 1986]
- Markus Rost.
Hilbert
90 for K3 for degree-two extensions.
Preprint, 1986.
- [Rost, 1988a]
- Markus Rost.
On
Hilbert Satz 90 for K3 for quadratic extensions.
Preprint, 1988.
- [Rost, 1988b]
- Markus Rost.
On the
spinor norm and A0(X,K1) for quadrics.
Preprint, 1988.
- [Rost, 1991]
- Markus Rost.
A
(mod 3) invariant for exceptional Jordan algebras.
C. R. Acad. Sci. Paris Sér. I Math., 313(12):823-827, 1991. MR 1138557
- [Rost, 1996]
- Markus Rost.
Chow
groups with coefficients.
Doc. Math., 1:No. 16, 319-393 (electronic), 1996. MR 1418952 [ORIGINAL
ARTICLE]
- [Rost, 1998]
- Markus Rost.
Chain lemma for splitting fields of symbols.
Preprint, 1998.
- [Rost, 1999]
- Markus Rost.
The
chain lemma for Kummer elements of degree 3.
C. R. Acad. Sci. Paris Sér. I Math., 328(3):185-190, 1999. MR 1674602 [ORIGINAL
ARTICLE]
- [Rost, 2000]
- Markus Rost.
Computations in the mod 2 lazard ring.
Preprint, 2000.
- [Scharlau, 1985]
- Winfried Scharlau.
Quadratic and Hermitian forms, volume 270 of Grundlehren
der mathematischen Wissenschaften.
Springer-Verlag, Berlin, 1985. MR 770063
- [Serre, 1962]
- Jean-Pierre Serre.
Corps locaux.
Actualités Sci. Indust., No. 1296. Hermann, Paris, 1962.
Publications de l'Institut de Mathématique de l'Université de Nancago,
VIII. MR 150130
- [Serre, 1979]
- Jean-Pierre Serre.
Local fields.
Springer-Verlag, New York, 1979.
Translated from the French by Marvin Jay Greenberg. MR 554237
- [Serre, 1994]
- Jean-Pierre Serre.
Cohomologie galoisienne, volume 5 of Lecture Notes in
Mathematics.
Springer-Verlag, Berlin, fifth edition, 1994. MR 1324577
- [Serre, 1995]
- Jean-Pierre Serre.
Cohomologie galoisienne: progrès et problèmes.
Astérisque, (227):Exp. No. 783, 4, 229-257, 1995.
Séminaire Bourbaki, Vol. 1993/94. MR 1321649
- [Serre, 1997]
- Jean-Pierre Serre.
Galois cohomology.
Springer-Verlag, Berlin, 1997.
Translated from the French by Patrick Ion and revised by the author. MR 1466966
- [Shibata, 1971]
- Katsuyuki Shibata.
On Boardman's generating sets of the unoriented bordism ring.
Osaka J. Math., 8:219-232, 1971. MR 298674
- [Shibata, 1973]
- Katsuyuki Shibata.
A note on the formal group law of unoriented cobordism theory.
Osaka J. Math., 10:33-42, 1973. MR 339204
- [Steenrod, 1962]
- N. E. Steenrod.
Cohomology operations.
Princeton University Press, Princeton, N.J., 1962.
Lectures by N. E. Steenrod written and revised by D. B. A. Epstein. Annals of
Mathematics Studies, No. 50. MR 145525
- [Stong, 1968]
- Robert E. Stong.
Notes on cobordism theory.
Princeton University Press, Princeton, N.J., 1968.
Mathematical notes. MR 248858
- [Suslin, 1982]
- A. A. Suslin.
Quaternion homomorphism for the field of functions on a conic.
Dokl. Akad. Nauk SSSR, 265(2):292-296, 1982.
[Soviet Math. Dokl. 26 (1982), no. 1, (1983), 72-77]. MR 665314
- [Suslin, 1987]
- A. A. Suslin.
Torsion in K2 of fields.
K-Theory, 1(1):5-29, 1987. MR 899915
- [Suslin, 1991]
- A. A. Suslin.
SK1 of division algebras and Galois cohomology.
In A. A. Suslin, editor, Algebraic K-theory, volume 4 of
Adv. Soviet Math., pages 75-99. Amer. Math. Soc., Providence,
RI, 1991. MR 1124627
- [Thom, 1954]
- René Thom.
Quelques propriétés globales des variétés différentiables.
Comment. Math. Helv., 28:17-86, 1954. MR 61823
- [Vishik, 1998]
- A. Vishik.
Integral motives of quadrics.
Preprint, Max-Planck-Institute for Mathematics, Bonn, 1998.
- [Voevodsky, 1996]
- V. Voevodsky.
The Milnor conjecture.
Preprint, Max-Planck-Institute for Mathematics, Bonn, 1996.
- [Wadsworth, 1986]
- Adrian R. Wadsworth.
Merkurjev's elementary proof of Merkurjev's theorem.
In Bloch et al. [Bloch et al.,
1986], pages
741-776. MR 862663
- [Weibel, 1997]
- Charles Weibel.
An introduction to
algebraic K-theory.
A graduate textbook in progress, 1997.
73 references, created using the perl script bib2html.
Powered by GNU Emacs
Updated: May 23, 2000
Contact: [email address]
Copyright © 1999, 2000 Markus Rost
Go to: Markus Rost's Web Page
![[image: colored graphic of triality, designed by H. Rost]](images/triality.jpg)
![[image: colored graphic of triality, designed by H. Rost]](images/triality.jpg)
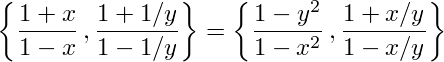
![]()