Periodische Funktionen und ihre Fourier-Entwicklung

• Jod-Konzentration in Butterfett in Abhängigkeit von der Jahreszeit. (Bliss Fig. 17.10)
  
  Das untere Bild liefert eine Sinuskurve, die als erste Approximation infrage kommt.
  
• Orientierung eines Vogels in der Nacht (und zwar eines migratory white-crowned sparrow). (Bliss Fig. 17.6)
  Auf der x-Achse sind hier die verschiedenen Himmelsrichtungen abgetragen.
  (Es handelt sich hier um einen Vogel, der in einem Rundkäfig eingesperrt ist; gemessen wird die Häufigkeit, mit der er versucht, in die jeweiligen Himmelsrichtungen zu fliegen.)
  
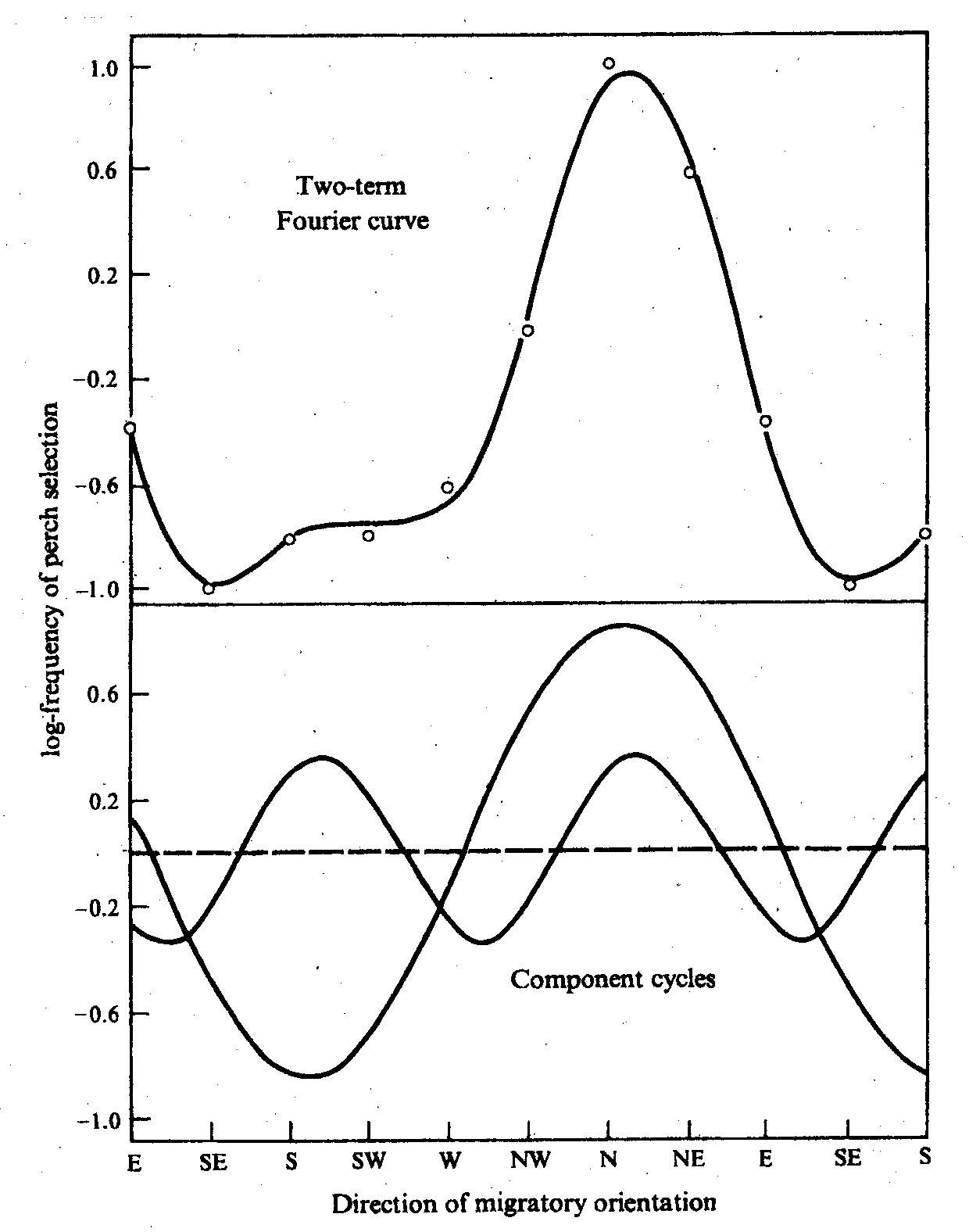
  Die obere Kurven ergibt sich als Summe der beiden Sinuskurven des unteren Bilds.
  Die Kurve kann durch folgenden Funktionsterm beschrieben werden:
      f(t) = -0,265 + 0,13 cos(t) - 0,86 sin(t) - 0,29 cos(2t) - 0,2 sin(2t)
• Auftreten von Kinderlähmungsfällen in den einzelnen Monaten. (jeweilige Mittelwerte über einen 15-Jahreszeitraum). (Bliss, Fig. 17.14)
  
  Die Kurve kann durch folgenden Funktionsterm beschrieben werden:
      f(t) = 1,85 - 0,64 cos(t) + 0,414 sin(t) - 0,027 cos(2t) - 0,086 sin(2t)