| Software: MAPLE (Differential-Gleichungen) |
with(DEtools):
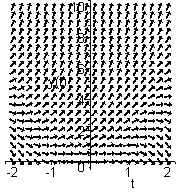
(dies sagt dem Rechner, dass Differentialgleichungen betrachtet werden). Wir wollen das Richtungsfeld (oder Vektorfeld) einer Differentialgleichung in einem t-y-Koordinatensystem zeichnen. Dazu gibt man zum Beispiel im Fall der Differentialgleichung
den Befehl ein:
dfieldplot(diff(y(t),t)=y(t)-t2,[y(t)],t=-2..2,y=0..10);
(dabei bedeutet t=-2..2 , dass man den Koordinatenbereich -2 < t < 2 sehen möchte, entsprechend steht y=0..10 für den Bereich 0 < y < 10). Als Ergebnis erhält man (nach einigem Warten):

phaseportrait(diff(y(t),t)=y(t)-t2,[y(t)],t=-1..2,[[y(-1)=1],[y(-1)=0.6]]);
Hier wird also durch den Zusatz [y(-1)=1] eine Lösung, die die Anfangswertbedingung y(-1)=1 erfüllt, eingezeichnet. Entsprechend liefert der zweite Zusatz [y(-1)=0.6] eine zweite Lösungskurve; beide Zusätze sind noch einmal geklammert: [ , ]. Das Ergebnis sieht so aus:
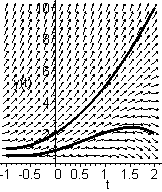
phaseportrait(diff(y(t),t)=y(t)-t2, [y(t)], t=-1..2, [[y(-1)=1], [y(-1)=0.6]], color=black, arrows=MEDIUM);