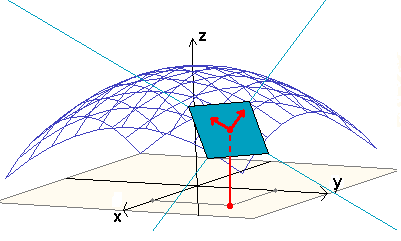
Hier eine Tangentialebene an eine Fläche im R3
(siehe www).
(1) Tangenten an den Graph einer differenzierbaren Funktion f(x) in einer Variablen x.
Die Tangente im Punkt (x0,f(x0) ist die Gerade durch den Punkt
(x0,f(x0) mit Richtungsvektor (1,λ) mit λ =
f'(x0),
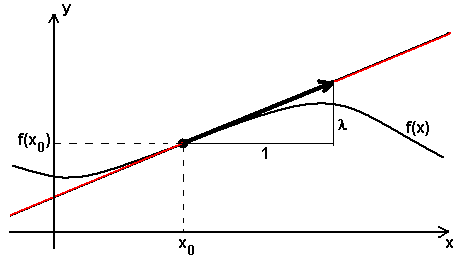
also die Menge aller Vektoren der Form
(x0,f(x0) + r(1,f'(x0))
mit r in R.
Man kann diese Vektoren natürlich auch in der Form
( x0 + r , f(x0) + rf'(x0) )
schreiben.
(2) Tangenten an den Graph einer partiell-differenzierbaren Funktion f(x,y) in zwei Variablen x,y.
Wir betrachten den Punkt (x0,y0,f(x0,y0)) auf dem Graphen
der Funktion f.
Wir können zwei Tangenten in diesem Punkt konstruieren, und zwar
- einmal in der Ebene der Punkte mit fester y-Koordinate y0,
- und zweitens in der Ebene der Punkte mit fester x-Koordinate x0.
Die erste Tangente erhält man durch
(x0,y0,f(x0,y0)) + r(1,0,fx(x0)),
mit r in R
(hier verwendet man also die partielle Ableitung fx in x-Richtung).
Die zweite Tangente erhält man durch
(x0,y0,f(x0,y0)) + r(0,1,fy(x0)),
mit r in R
(hier verwendet man also die partielle Ableitung fy in y-Richtung).
Diese beiden Tangenten haben die gleiche Form wie die Tangenten, die in (1) angegeben wurden
(der einzige Unterschied besteht darin, dass jeweils eine zusätzliche konstante Koordinate
mitgeschleppt wird).
(3) Tangentialebenen an den Graphen einer differenzierbaren Funktion f(x,y) in zwei Variablen x,y.
Dass f differenzierbar ist, besagt gerade, dass derartige Tangentialebenen existieren.
Man erhält
eine derartige
Tangentialebene, indem man die Ebene nimmt, die durch die beiden unter (2) konstruierten Tangenten
erzeugt wird:
(x0,y0,f(x0,y0)) + r(1,0,fx(x0)) +
s(0,1,fy(x0)),
mit r,s in R.
biomath

