Funktionen in zwei Variablen

Ist eine Funktion f(x,y) in den zwei Variablen x,y gegeben, so betrachten man oft die Einschränkungen von f auf achsenparallele Geraden:

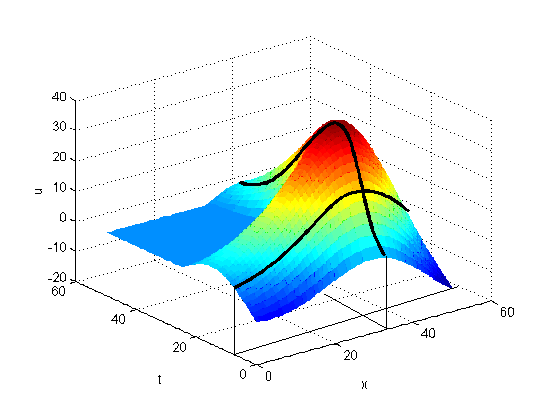
Partiell differenzierbar, unbeschränkt in der Nähe des Ursprungs

> plot3d(x/(x^2+y^2), x=-1..1, y=-1..1, view 0..1, axes=boxed);

Die partielle Ableitung f_y(x,y) existiert für alle (x,y), denn die Funktion y |-> f(x₀,y) ist für alle Werte x₀ differenzierbar:

dies ist klar für x₀ ≠ 0;
für x₀ = 0 ist aber nichts zu zeigen, denn es handelt sich ja dann um die Nullfunktion.

Entsprechend ist die Funktion xy/(x^2+y^2)^2 sowohl in x-Richtung als auch in y-Richtung partiell ableitbar - und ebenfalls in (0,0) nicht stetig.

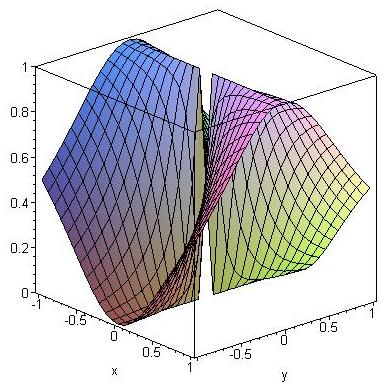
Partiell differenzierbar, beschränkt, nicht stetig ergänzbar im Ursprung

> plot3d(x^2/(x^2+y^2), x=-1..1, y=-1..1, view=-20..20, axes=boxed);

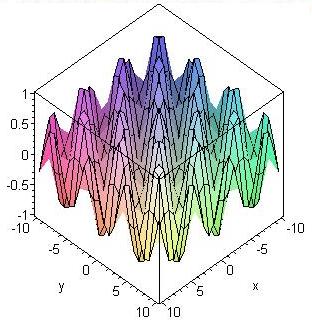
Viele Minima und maxima

> plot3d(sin(x)*sin(y), x=-10..10, y=-10..10, axes=boxed);

Sattelpunkt

> plot3d(x*y, x=-1..1, y=-1..1, view=-1..1, axes=boxed);

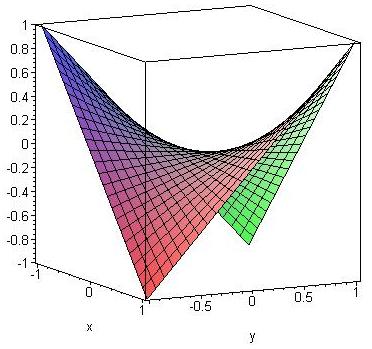
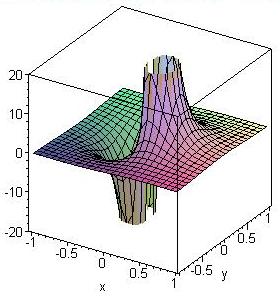
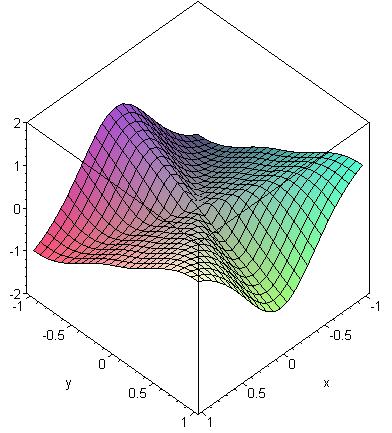
Nicht-vertauschbare partielle Ableitungen

> plot3d(x*y*(x^2-y^2)/(x^2+y^2), x=-2..2, y=-2..2, view=-1..1, axes=boxed);

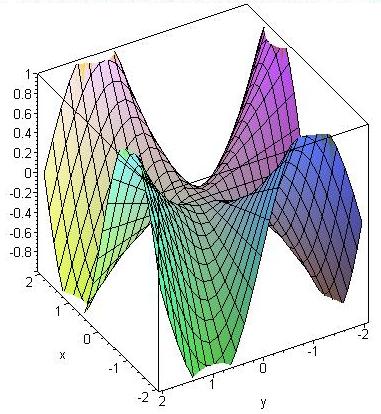
Es ist f_xy(0,0) = -1, aber f_yx(0,0) = 1.

Außerhalb des Punkts (0,0) gilt:

f_xy = f_yx = (x⁶ + 9x⁴y² - 9x²y⁴ -y⁶)/(x² + y²)³ diese Funktion ist aber eben in (0,0) nicht stetig ergänzbar:
> plot3d((x^6+9*x^4*y^2-9*x^2*y^4-y^6)/(x^2+y^2)^3, x=-1..1, y=-1..1, view=-2..2, axes=boxed);

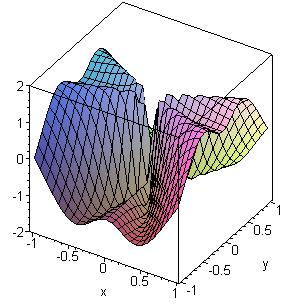
Es ist f_y = (x⁵-4x³y²-xy⁴)/(x²+y²)²

Insbesondere ist f_y(x,0) = x⁵/x⁴ = x, also f_yx(0) = +1.

Und es ist f_x = (x⁴y+4x²y³-y⁵)/(x²+y²)²

Insbesondere ist f_x(0,y) = -y⁵/y⁴ = -y, also f_xy(0) = -1.

biomath