Musterlösung der Aufgabe 5.4


# Pakete für Lineare Algebra (Matrix) und Zahlentheorie einbinden
with(linalg):
with(numtheory):
 
# Die Tabelle wird in Form einer Matrix gespeichert. Dabei ist zu
# beachten, daß die erste Zeile der Matrix Index 1 hat, die
# Restklassen a aber mit 0 beginnen - die Zahlen für Restklasse a
# werden daher in Zeile a+1 gespeichert.
#
# Größe der Tabelle festlegen und ausgeben
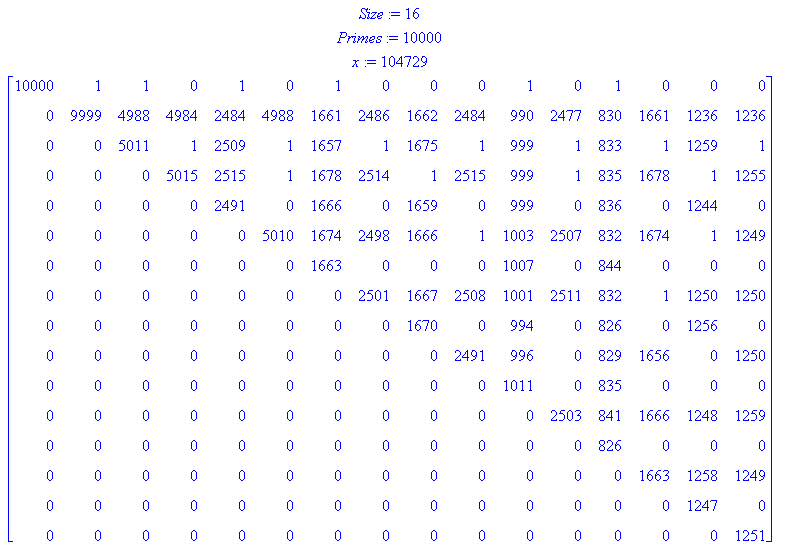
Size := 16;
# Anzahl der Primzahlen festlegen und ausgeben
Primes := 10000;
# Maximale Primzahl ausgeben
x := ithprime(Primes);
# Tabelle vorbereiten: Größe ist Size x Size, alle Einträge sind Null
Table := matrix(Size,Size,0):
for i from 1 to Primes do
  # i-te Primzahl p bestimmen
  p := ithprime(i):
  for k from 1 to Size do
     # Restklasse a von p modulo k bestimmen
     a := irem(p, k):
     # Tabelleneintrag für (a,k) erhöhen
     Table[a+1,k] := Table[a+1,k] + 1:
  od:
od:
# Tabelle ausgeben
print(Table);

Anmerkung: Wir betrachten hier die ersten 10000 Primzahlen, also die Primzahlen 2, 3, 5, ... , 104729 (= x). Schaut man sich in den einzelnen Spalten die von 0 und 1 verschiedenen Einträge an, so stellt man fest, dass sich diese Einträge einer festen Spalte nur geringfügig unterscheiden. Die Summe aller Einträge in einer Spalte ist gleich 10000. Die Anzahl der von 0 und 1 verschiedenen Einträge in der k-ten Spalte ist φ(k), also kann man vermuten:

Vermutung: Jeder von 0 und 1 verschiedene Eintrag in der k-ten Spalte ist ungefähr 10000/φ(k).