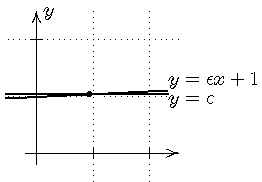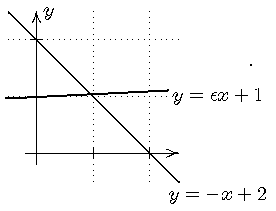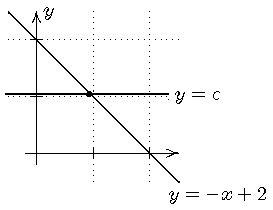| -εx | + | y | = | 1 |
| (1+1/ε)y | = | 2+1/ε |
| y | = | c |
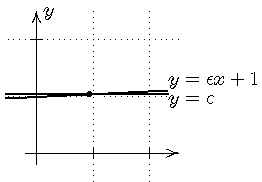
- für ε = 10-9 ergibt sich als
exakte Lösung:
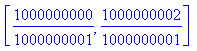 ,
,
Maple (voreingestellt mit einer Rechengenauigkeit von 10 Stellen) liefert ein zufriedenstellendes Ergebnis. - für ε = 10-10 ergibt sich als
exakte Lösung:
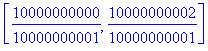 ,
,
Maple (voreingestellt mit einer Rechengenauigkeit von 10 Stellen) liefert ein völlig falsches Ergebnis.
Erläuterung: Gesucht wird nach den Schnittpunkten der Geraden
| y = | εx + 1 |
| y = | c |
Ist ε sehr klein (also gegenüber 1 "vernachlässigbar"), so wird mit c = 1 gerechnet.
Setzen wir aber c = 1, so ergibt sich x = 0.
Dass die Berechnung des Schnittpunkts zweier Geraden,
die fast die gleiche Steigung haben, zu Problemen führen kann, ist klar!
Und in unserem Fall handelt es sich um eine solche Situation: