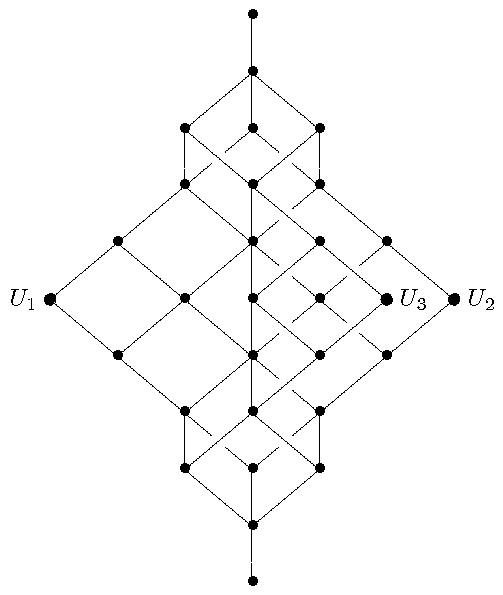

For better understanding of this lattice, let us single out some
parts of the lattice using different colours:
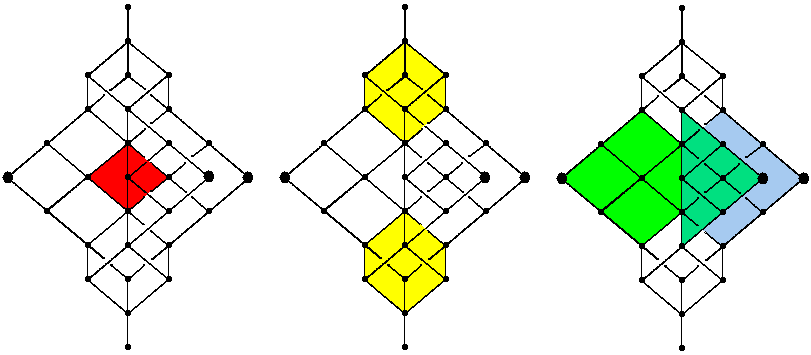
Of particular interest are the following two subspaces called
D and E in the lecture (in contrast to most of the other
subspaces, these two remain invariant, when we renumber the
given subspaces U1, U2, U3).
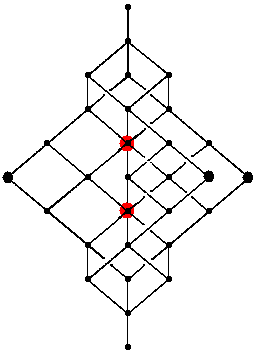
|
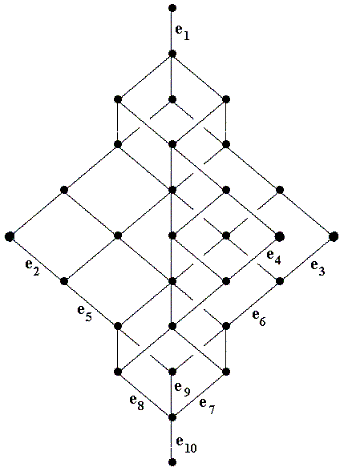
One obtains this subspace lattice for the following subspace triple:
Let k be a field, let V = k10 (with standard basis e1,..., e10), and let
On the right, we show for some edges (they
symbolize inclusions of subspaces) some elements of the
standard basis: If the edge connects (going upwards) the
bullet V' with the bullet V" (thus V' is a subspace of V")
and if we mark this edge with the element ei, then
this means that V'+< ei > = V".
| 
|
|
The structure of this lattice was exhibited by Dedekind in
a paper published in the year 1900
(Über die von drei Moduln erzeugte Dualgruppe, Math. Ann.
53 (1900), 371-403.), it is the free modular lattice in 3
generators
It is not known how the corresponding free modular lattice in 4 generators (or the subspace lattices generated by 4 subspaces U1, U2, U3, U4) may look like. |
|
Gian-Carlo Rota wrote in 1997:
The free modular lattice with three generators (which has twenty-eight elements) is a beautiful construct that is presently exiled from textbooks in linear algebra. Too bad, because the elements of this lattice explicitly describe all projective invariants of three subspaces. |