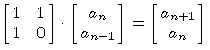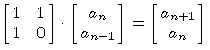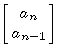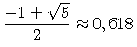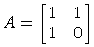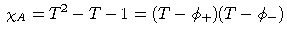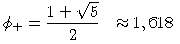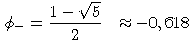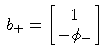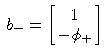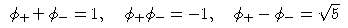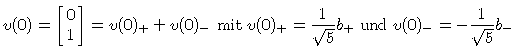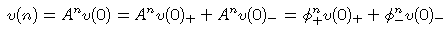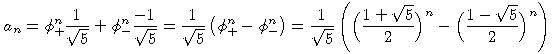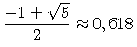Fibonacci-Zahlen
Fibonacci-Folgen: Dies sind Folgen (an)n reeller
Zahlen, die folgendermaßden definiert sind:
Seien a0, a1 reelle Zahlen.
Definiere induktiv für n ≥ 2
an+1 = an + an-1 für n ≥ 1
Anders ausgedrückt:
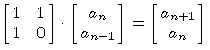
Sei nun a0 = 0, a1 = 1.
Frage: Wie groß ist beispielsweise a40? oder auch
a300 ?
Es ist a40 =
102.334.155 = 3 x 5 x 7 x 11 x 41 x 2161
Und a300=
222232244629420445529739893461909967206666939096499764990979600
Für n ≥ 1 sei
|
v(n) =
| 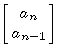
|
Dies ist also ein Vektor in R2.
Hier die ersten 8 Vektoren v(1),...,v(8):
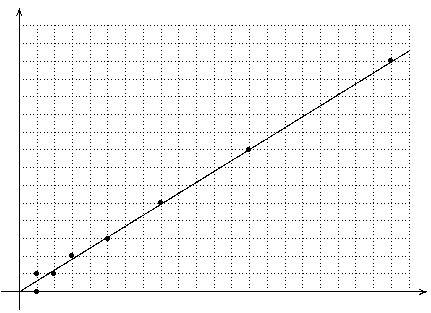
Sie liegen alle in der Nähe der Geraden mit Steigung
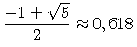
(man kann das folgendermaßen formulieren: der angegebene Wert ist gerade lim an-1/an)
und zwar "pendeln" sie um diese Gerade - warum?
Wir operieren hier mit der Matrix
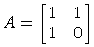 auf der Ebene R2.
Es gilt:
auf der Ebene R2.
Es gilt:
| Das charakteristische Polynom ist | 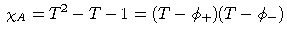
|
| es hat die Eigenwerte | 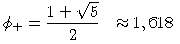 | und
| 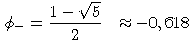
|
| und Eigenvektoren | 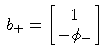 | | 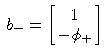
|
Für die Eigenwerte gelten die folgenden Rechenregeln:
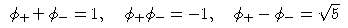
Es empfiehlt sich, zusätzlich auch den folgenden Vektor zu betrachten:
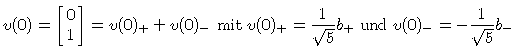
Es gilt also für alle n ≥ 0:
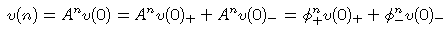
denn
- v(0)+ ist Eigenvektor mit Eigenwert φ+,
- v(0)- ist Eigenvektor mit Eigenwert φ-,
Betrachten wir nur die erste Koordinate (die x-Koordinate) von v(n),
so erhalten wir:
Man nennt dies die Formel von Binet (er hat sie 1842 publiziert, sie war
aber vorher schon Euler und D. Bernoulli bekannt).
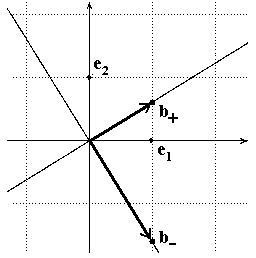
Hier, zur Verdeutlichung die Vektoren v(0),...,v(4):
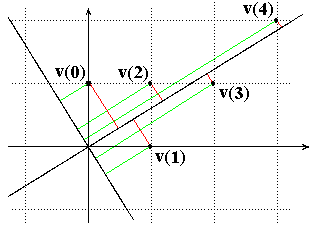
Die beiden schrägen Geraden sind die Eigengeraden der Matrix A.
Es wird für jeden der Vektoren v(0),...,v(4)
gezeigt, wie er sich als Summe eines Vektors in der Eigengerade
g+ = Rb+
und eines Vektors in der Eigengerade g- = Rb-
schreibt:
v(n) = v(n)++v(n)- mit
v(n)+ in g+ und v(n)- in g-
(Die grüne Strecke ist jeweils (parallel zu) v(n)+, die rote ist
(parallel zu) v(n)-.)
Und es gilt:
v(n+1)+ = λ+v(n)+ und
v(n+1)- = λ-v(n)-
Die Länge der Vektoren v(n)- konvergiert gegen 0,
also unterscheidet sich v(n) von v(n)+ für großes n
nur ganz wenig.
Da man ja weiß, dass v(n) ein ganzzahliger Vektor ist,
kann man auf diese Weise v(n) exakt berechnen! Dabei interessiert uns
nur die x-Koordinate von v(n), denn dies ist die i-te Fibonacci-Zahl
an.
Weitere Information
Fakultät für Mathematik, Universität Bielefeld
Verantwortlich: C.M.Ringel
E-Mail:
ringel@mathematik.uni-bielefeld.de